Continuing, we last saw that the corresponding nonlinear sigma model can be truncated to a version that involves only four scalars and characterizes the Klebanov-Strassler solution. Letting the fields be denoted by ![]() , then
, then ![]() measures the
measures the ![]() volume and
volume and ![]() the ratio of scales between the 2-cycle and the 3-cycle;
the ratio of scales between the 2-cycle and the 3-cycle; ![]() the dilaton, and
the dilaton, and ![]() measures the
measures the ![]() potential. Then the 5-D action is
potential. Then the 5-D action is
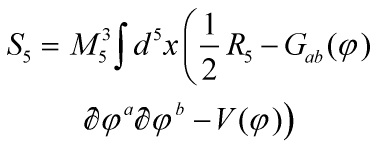
![]() and
and ![]() are constants, with
are constants, with ![]() proportional to the number of 3-form flux quanta
proportional to the number of 3-form flux quanta ![]() , and with a warped ansatz as in
, and with a warped ansatz as in
![]()
for the 5-D metric, a solution to the equations of motion is given by the Klebanov-Strassler background
![]()
and the warp factor given by the first and last terms of the potential in
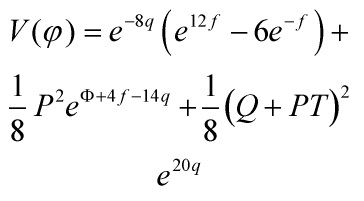
allowed us to establish a quasi-morphism between the the Klebanov-Strassler throat and Randall-Sundrum geometry.
I have shown that these warped regions admit a 5d Randall-Sundrum model interpretation with a large hierarchy between the UV and IR brane and can be taken as an implementation of the Goldberger-Wise scalar mechanism.
- Let the UV brane denote the compact space and conical region…
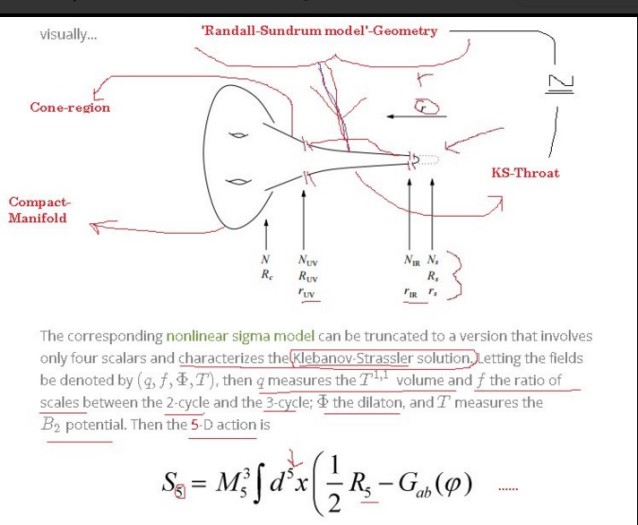
From a 10d perspective, this is the area where the warp factor is constant. Hence the universal Kähler modulus simply corresponds to an overall rescaling of this space. In particular, for
![Rendered by QuickLaTeX.com \[\int\limits_{{T^{1,1}}\,{\rm{at}}\,{\rm{r = }}{{\rm{R}}_c}} {{{\tilde F}_5}} \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e87d74174fe661e51ef63d0b48c05ed2_l3.png)
the flux number
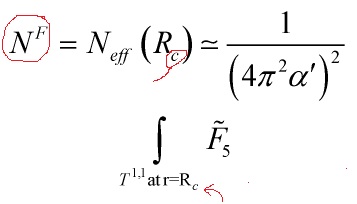
is invariant under this rescaling and from the point of view of the throat, it is determined by the localized sources and flux in the compact space ![]() ‘s submanifold
‘s submanifold ![]() . Isolating the conical region and the throat, one demands on always using coordinates such that the warp factor in the conical region is unity as in
. Isolating the conical region and the throat, one demands on always using coordinates such that the warp factor in the conical region is unity as in
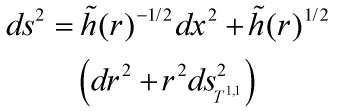
and
![]()
then ![]() can be identified with the universal Kähler modulus, which fixes
can be identified with the universal Kähler modulus, which fixes ![]() in terms of
in terms of ![]() . This gives the warp factor
. This gives the warp factor
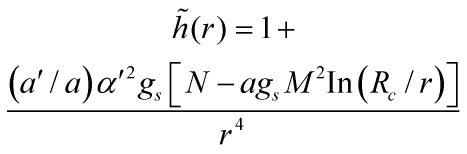
The boundary between the conical region and the throat, ![]() , is then determined by the solution of the equation
, is then determined by the solution of the equation
![]()
and assuming that, at this boundary, the logarithmic term in
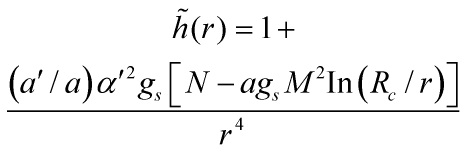
is small relative to N and working to leading order in this small term, we find
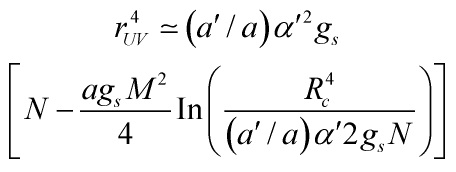
Hence, the conical region shrinks to zero size if ![]() takes the value
takes the value
![]()
- In the large-hierarchy case, the last expression is roughly equal to the inverse warp factor and is hence extremely large: there is a large range in which the variation of
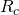 , of the universal Kähler modulus, has very little effect on the throat length, as expressed by the above equation and it follows from the 5d point of view that the universal Kähler modulus is a field localized at the UV brane.
, of the universal Kähler modulus, has very little effect on the throat length, as expressed by the above equation and it follows from the 5d point of view that the universal Kähler modulus is a field localized at the UV brane.
So, the fundamental scale is the reduced 5d Planck mass defined by ![]() , which, near the UV brane, is related to
, which, near the UV brane, is related to ![]() by
by
![]()
and we can identify ![]() with
with ![]() , giving us
, giving us
![]()
and the physical length ![]() of the throat is given by
of the throat is given by
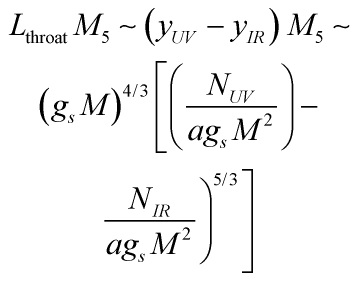
where ![]() is the flux at the small end of the conical region with
is the flux at the small end of the conical region with
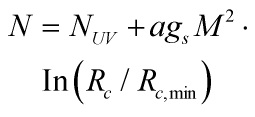
- We are now in a position to construct the Randall–Sundrum 5d type effective action including bulk and brane fields.
For ![]() , the integral over the compact space at the UV-end of the throat contributes
, the integral over the compact space at the UV-end of the throat contributes
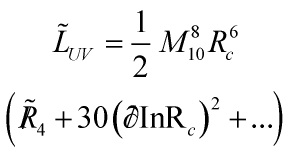
to the 4d effective action and note the 4d metric implicit in ![]() is simply the 4d part of the 10d metric in the Einstein frame: no Weyl rescaling needed. Now writing the 5d metric as
is simply the 4d part of the 10d metric in the Einstein frame: no Weyl rescaling needed. Now writing the 5d metric as
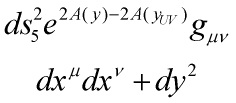
and integrating from ![]() to
to ![]() , we contribute to the following piece the Einstein-Hilbert-term of the 4d action
, we contribute to the following piece the Einstein-Hilbert-term of the 4d action
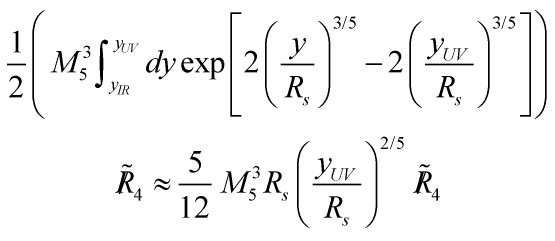
Eq. (48)
- Note that the relative normalization of the coefficients of the
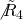 and the
and the 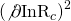 terms equation
terms equation
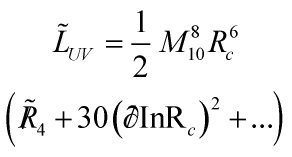
Eq. (46)
is analytically linked to the fact that ![]() is the imaginary part of a superfield
is the imaginary part of a superfield ![]() , which is an integral part of a no-scale supergravity model. For consistency with Eq. (48), the coefficient of the
, which is an integral part of a no-scale supergravity model. For consistency with Eq. (48), the coefficient of the ![]() term in Eq. (46) has to be modified according to
term in Eq. (46) has to be modified according to
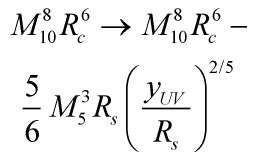
Eq. (49)
Now define
![]()
The action now reads
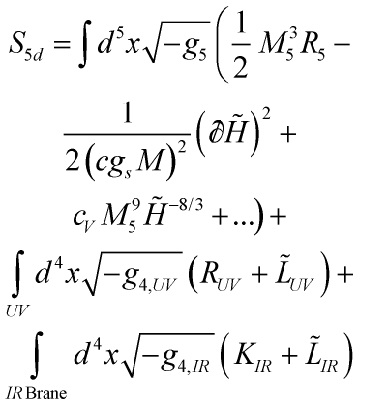
Eq. (51)
with ![]() the trace of the extrinsic curvature: the Gibbons-Hawking surface term, and
the trace of the extrinsic curvature: the Gibbons-Hawking surface term, and ![]() the induced metric at each of the 4d boundaries. Hence, the brane Lagrangians are
the induced metric at each of the 4d boundaries. Hence, the brane Lagrangians are
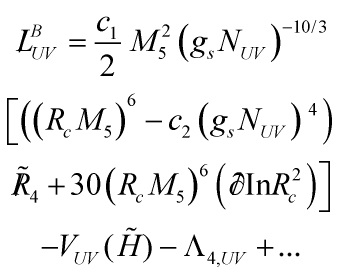
Eq. (52)
and
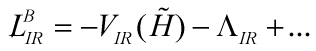
Eq. (53)
with the coefficients
![]()
where ![]() and
and ![]() are super-steep potentials setting
are super-steep potentials setting ![]() to its values at the UV and IR brane respectively, as
to its values at the UV and IR brane respectively, as
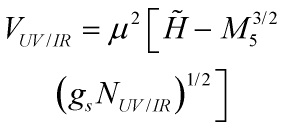
Eq. (54)
with a very large coefficient ![]() . The brane tensions or 4d brane cosmological constants
. The brane tensions or 4d brane cosmological constants ![]() and
and ![]() have values
have values
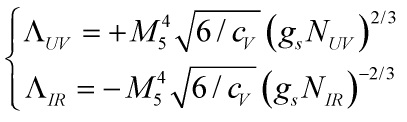
Eq. (55)
The fundamental dynamics of the throat can be understood from the 5d action of Eq. (51): the scalar field ![]() dominates, via the potential term, the AdS curvature and hence the warping. The rapidity with which the curvature changes as one moves along the 5th dimension is determined by the coefficient of the kinetic term for
dominates, via the potential term, the AdS curvature and hence the warping. The rapidity with which the curvature changes as one moves along the 5th dimension is determined by the coefficient of the kinetic term for ![]() . In the limit of vanishing M, no change is can occur – this is the pure
. In the limit of vanishing M, no change is can occur – this is the pure ![]() case. The brane values of
case. The brane values of ![]() are determined by steep brane potentials. The IR-brane potential models the Klebanov-Strassler region. The UV-brane potential models the way in which the various string-y and field-theoretic sources of D3– brane flux in the compact space determine
are determined by steep brane potentials. The IR-brane potential models the Klebanov-Strassler region. The UV-brane potential models the way in which the various string-y and field-theoretic sources of D3– brane flux in the compact space determine ![]() in the conical region. The combined dynamics of UV/IR-brane and 5d bulk actions thus stabilizes the length of the interval and fixes the hierarchy.
in the conical region. The combined dynamics of UV/IR-brane and 5d bulk actions thus stabilizes the length of the interval and fixes the hierarchy.
- We can now explicitly relate the parameters of our 5d description, the boundary scalar
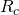 and the 5d radion
and the 5d radion
![]()
to the corresponding standard string moduli. Zeroing in on the universal Kähler modulus ![]() and a single complex structure modulus
and a single complex structure modulus ![]() , the 4d N = 1 superfield action is determined by the Kähler potential
, the 4d N = 1 superfield action is determined by the Kähler potential
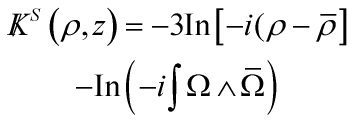
Eq. (56)
and the superpotential
![]()
where
![]()
and the imaginary part of the universal Kähler modulus governs the compactification volume. So the 4d no-scale field ![]() is related to
is related to ![]() via
via
![]()
Hence, the relation of the complex structure modulus ![]() to the relative warping between the UV and IR region is found to be
to the relative warping between the UV and IR region is found to be
![]()
So the relative 5d warping is
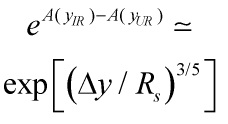
Eq. (61)
yielding ![]() through the 5d radion as
through the 5d radion as
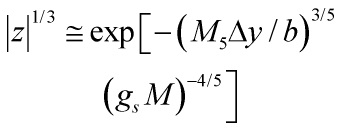
Eq. (62)
- The essential quantity on the 5d side is the radion superfield
 with
with 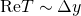
Therefore, the Kähler potential in terms of ![]() is
is
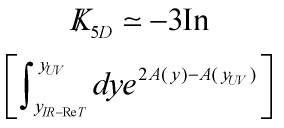
Eq. (63)
and is proportional to the logarithm of the coefficient of the Ricci scalar in the 4d effective action before Weyl rescaling, and so we can derive
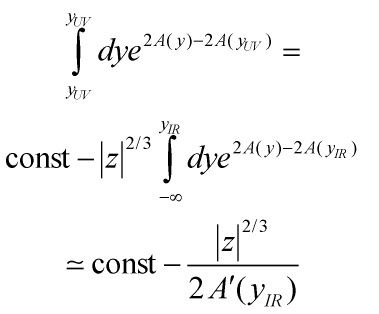
Eq. (64)
and given that
![]()
Eq. (64) implies for the ![]() -dependent part of the Kähler potential that
-dependent part of the Kähler potential that
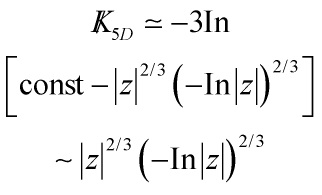
Eq. (65)
supressing the prefactor and subdominant terms, the relevant cycles of the compactification manifold are the conifold 3-cycle with period ![]() and its dual
and its dual ![]() with period
with period
![]()
With the warp factor contribution at the tip given by
![]()
‘putting’ Eq. (62), Eq. (63), Eq. (64), and Eq. (65), with Eq. (46), we obtain for the ![]() -dependent part
-dependent part
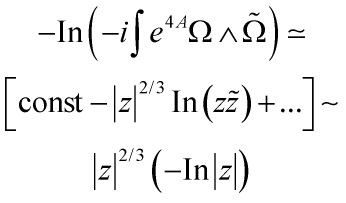
Eq. (67)
Hence arriving at our effective Randall-Sundrum 5D Brane action
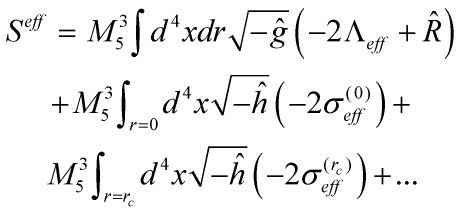
RS-5d-A
yielding a cosmological quasi-morphicity that describes our universe as a five-dimensional anti-de Sitter space and the field-ontology ‘lives’ locally on a (3 + 1)-dimensional brane minus the graviton … for another day!


