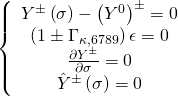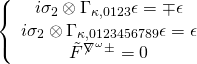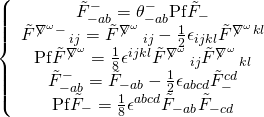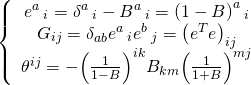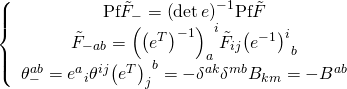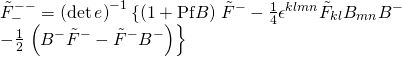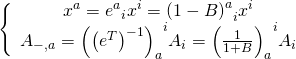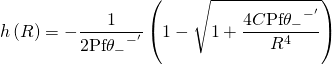In part III, we completed the derivation of the Standard ΛCDM Model of cosmology from Type-IIB SUGRA with a Horava-Witten embedding in M-theory. However, we must also account for the de Sitter valley Coulomb gauge-phase as well as the Higgs waterfall gauge-phase leading to the ground state Einstein-Sasaki-Minkowski vacuum. As of yet, only M-theory can incorporate both phases. Here, we shall derive such phases based on a Type-IIB 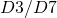 system. Let us recall the main mathematical results of part III. Starting with our action:
system. Let us recall the main mathematical results of part III. Starting with our action:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=\int{{{{d}^{4}}}}x\sqrt{{-{{g}_{E}}}}\left[ {-\frac{1}{4}} \right.{{\left( {{{F}_{W}}} \right)}^{2}}-\frac{1}{4}{{\left( {{{F}_{{{W}'}}}} \right)}^{2}}-\\{{\left| {\partial S} \right|}^{2}}-{{\left| {\partial {S}'} \right|}^{2}}-{{R}^{{-12}}}\frac{1}{{8g_{7}^{2}}}\int_{{K3}}{{{{{\tilde{F}}}^{D}}^{-}\wedge *{{{\tilde{F}}}^{D}}^{-}}}-\\{{\left| {{{D}_{\mu }}\chi } \right|}^{2}}-2{{g}^{2}}{{\left| S \right|}^{2}}{{\left| \chi \right|}^{2}}\left. {-\frac{{\left( {g_{3}^{2}+\tilde{g}_{3}^{2}} \right)}}{2}{{{\left( {{{\chi }^{\dagger }}{{\sigma }^{A}}\chi } \right)}}^{2}}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-daa9b8f3bdc50e63050642e211f74c8f_l3.png)
we take M-theory with  parallel
parallel  branes spread along the orbifold
branes spread along the orbifold  , which preserves
, which preserves  SUSY in 4-D, with the wrapped 6-D background along
SUSY in 4-D, with the wrapped 6-D background along  . Each
. Each  brane fills the 4-D non-compact spacetime and wraps the same holomorphic two-cycles
brane fills the 4-D non-compact spacetime and wraps the same holomorphic two-cycles  on the Calabi-Yau. The main terms of the 4-D
on the Calabi-Yau. The main terms of the 4-D  SYM theory are the volume modulus of the Calabi-Yau:
SYM theory are the volume modulus of the Calabi-Yau:
the length modulus:
and the

brane chiral superfields:
where
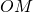
stands for ‘open membrane’. Then we derived the

-term from the

parallel brane system that supports the

5-branes as such. The

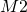
Lagrangian is:
with
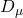
the covariant derivative:
and

the Kähler potential, and the Chern-Simons term
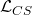
for the gauge potential is given by:
where

define the brane transverse directions. The SUSY transformations are:
with gauge conditions:
which promote the system to a 6D

SYM system with a Lagrangian:
where:
and
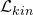
is given in terms of the kinetic terms for the
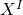
‘s:
with:
and
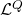
is given as such:
and where the relevant gauge field term is given by:
with the Hodge dual field strength is given by:
Thus, the equations of motion from

are:
Combining with the Bianchi identity:
gives us:
The term for the

-field whose existence follows from the
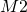
-Lagrangian, is:
Thus, we get:
giving us solutions of the form:
Integrating, we get the
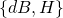
terms, which, in our

system, satisfy:
as well as:
Plugging in the Kähler potential, we can derive the

chiral super-field

-term action:
with:
with the covariant derivative:
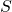
is the neutral

gauge field charge,

is the
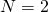
hypermultiplet charged under

gauged by the
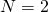
vector multiplet

with superpotential and

-term that drive inflation:
dynamically as a function of kinetic terms of type
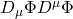
. The proof proceeds by plugging the RG-flow equation with the Hubble and inflaton term factored quadratically, with the

-term potential:
Thus, the fermionic contributions to the inflaton field derive from the transformations:
and where the
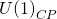
gravitino connection
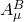
is:
which reduces to:
Now, by integrating the

chiral super-field

-term:
we get the

-term:
with:
Let us start our embedding of
hybrid inflation. First, note that a
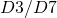
brane system in the presence of Fayet-Illiopoulos parameter becomes unstable unless it is a completely coincident system. Take the

brane world volume action:
with:
where

is the pull-back of the NS-NS 2-form and
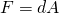
is the Born-Infeld field strength. Now put the

brane in a
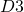
brane background. We get, for constant dilaton and metric:
and for the self-dual RR form:
where
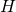
is the central Hodge harmonic function on
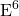
with
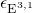
the volume form on
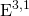
, while factoring in the

brane worldvolume gauge fields. Thus, our effective potential is given by:
If the angles
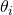
are equal, the force between the
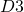
brane and the

brane vanishes, giving us a 4-D Euclidean self-dual system in the 6 and 9 directions. In polar coordinates, we hence have:
where
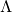
is the renormalization group cutoff, and
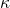
-symmetry allows us to deduce manifest supersymmetry breaking associated to the Yang-Mills field strength of the
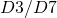
brane system. Our bosonic action is given by:
and some solutions must have some unbroken SUSY since there exists solutions to the kappa-symmetry equation:
where
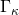
is the
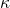
-symmetry projection operator for a

brane in a
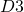
worldvolume background:
and
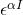
is a Type IIB spinor with a chiral bi-Majorana spinor representation, and
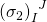
is a Pauli matrix and in the absence of non-zero contorsion factor for

, the Killing equation reproduces the

-brane projector:
corresponding to half of the unbroken supersymmetry. We hence have a skew-diagonal configuration with
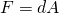
on the worldvolume, and the matrix
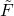
is antisymmetric and independent on the worldvolume coordinates:
with:
and the vielbeins are given by the
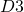
-brane metric and the
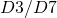
brane-system Killing spinors condition is:
The Killing spinor satisfies, in the presence of a
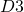
background, the following two conditions:
that break half the supersymmetry, which reduce:
to:
The
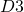
brane worldvolume Hodge-Dirac harmonic function at the

loci
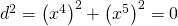
is:
Hence, the Killing equation has solution of type:
noting that in the Coulomb phase, unlike the Higgs phase,
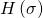
is a function of the

-brane worldvolume coordinates and thus determined by the RR-RR and NS-NS forms. Any such configuration of
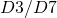
branes must be unstable. To see why, consider a

brane probed by a
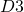
brane with

field satisfying
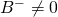
. A SUSY solution gotten via mirror symmetry at the
Hitchin holomorphic angles has the form:
and we have:
We then find that the
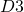
brane action is given by:
where we have implicitly defined
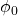
by
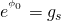
, and our potential is given by:
in light of the gauge-invariance of:
Now consider the

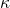
-symmetric Dirac-Born-Infeld/WZ action above, and a
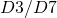
supersymmetric bound state for a given
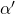
and embed the

brane in the full Minkowski 10D space. The SUSY equation is then:
In the Coulomb hybrid phase, we pick an everywhere skew diagonal basis for
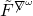
, and in the Higgs phase, it can be allowed to be a function of the worldvolume coordinates. Hence
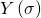
is a highly non-linear term given by:
Thus, the Killing spinor equation reduces to:
with constant spinors. There are two ways to preserve SUSY. With an
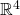
chiral/anti-chiral spinor satisfying the conditions:
and with a spinor satisfying the equation:
Now since the supersymmetric configurations in the Higgs branch are given by:
the solution necessarily has chiral spinors in Minkowski 4D spacetime and our system is equivalent to a
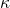
-symmetric Euclideanized
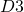
brane dissolved into a

brane, as implied by the following relation:
Conjugation gives us the results in the Coulomb branch of hybrid inflation. We are now in a position to analyze a non-linear Seiberg-Witten solution to the above BPS equation. We put it in canonical Moriyama form:
and our frame metric is defined implicitly via the open string metric:
and the vierbein and non-Abelian theta parameter are given by:
respectively and the frame-Pfaffian equations are given by:
We can now derive the identity:
hence our BPS equation reduces to:
To solve, note that
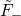
can be defined in terms of the frame coordinates and the gauge potential as such:
hence, a solution to:
takes the form:
with:
In the presence of the RR field, the

-instanton gets a blow-up, and ceases to be singular and we get a UV non-linear Seiberg-Witten gauge equation:
Thus, the non-vanishing

is our cosmological potential seed that also defines a positive vacuum energy. Thus we get a hybrid slow-roll inflation stage where our pocket-universe goes through a waterfall condensation stage, and eventually settles into the Minkowski vacuum described by a bound state of
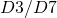
branes corresponding to the Higgs phase of the gauge theory with the FI term defined by

. Since
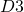
living on

branes can be interpreted as instantons due to Chern-Simons gauge coupling:
the Higgs phase above is hence equivalent to a noncommutative Nekrasov-ADHM non-linear instanton in M-theory, and we have an intrinsic connection between the cosmological constant in 4D and the noncommutative

parameter in internal space 6789. Next, we do a Type-IIB compactification and an uplift to M-theory.
![]() system. Let us recall the main mathematical results of part III. Starting with our action:
system. Let us recall the main mathematical results of part III. Starting with our action:![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=\int{{{{d}^{4}}}}x\sqrt{{-{{g}_{E}}}}\left[ {-\frac{1}{4}} \right.{{\left( {{{F}_{W}}} \right)}^{2}}-\frac{1}{4}{{\left( {{{F}_{{{W}'}}}} \right)}^{2}}-\\{{\left| {\partial S} \right|}^{2}}-{{\left| {\partial {S}'} \right|}^{2}}-{{R}^{{-12}}}\frac{1}{{8g_{7}^{2}}}\int_{{K3}}{{{{{\tilde{F}}}^{D}}^{-}\wedge *{{{\tilde{F}}}^{D}}^{-}}}-\\{{\left| {{{D}_{\mu }}\chi } \right|}^{2}}-2{{g}^{2}}{{\left| S \right|}^{2}}{{\left| \chi \right|}^{2}}\left. {-\frac{{\left( {g_{3}^{2}+\tilde{g}_{3}^{2}} \right)}}{2}{{{\left( {{{\chi }^{\dagger }}{{\sigma }^{A}}\chi } \right)}}^{2}}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-daa9b8f3bdc50e63050642e211f74c8f_l3.png)
![]() parallel
parallel ![]() branes spread along the orbifold
branes spread along the orbifold ![]() , which preserves
, which preserves ![]() SUSY in 4-D, with the wrapped 6-D background along
SUSY in 4-D, with the wrapped 6-D background along ![]() . Each
. Each ![]() brane fills the 4-D non-compact spacetime and wraps the same holomorphic two-cycles
brane fills the 4-D non-compact spacetime and wraps the same holomorphic two-cycles ![]() on the Calabi-Yau. The main terms of the 4-D
on the Calabi-Yau. The main terms of the 4-D ![]() SYM theory are the volume modulus of the Calabi-Yau:
SYM theory are the volume modulus of the Calabi-Yau:

![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{\mathcal{L}}^{Q}}=-\frac{1}{2}\left[ {{{{\left( {{{\partial }_{\mu }}{{X}^{i}}} \right)}}^{2}}+{{{\left( {{{\partial }_{{\dot{\mu }}}}{{X}^{i}}} \right)}}^{2}}} \right]+\\\frac{i}{2}\left\langle {\bar{\Psi },\left( {{{\Gamma }^{\mu }}{{\partial }_{\mu }}+{{\Gamma }^{{\dot{\mu }}}}{{\partial }_{{\dot{\mu }}}}} \right)\Psi } \right\rangle -\\\frac{1}{4}{{F}_{{\mu \dot{\nu }\dot{\lambda }}}}^{2}-\frac{1}{{12}}{{F}_{{\dot{\mu }\dot{\nu }\dot{\lambda }}}}^{2}-\frac{1}{2}{{\epsilon }^{{\mu \nu \lambda }}}{{\epsilon }^{{\dot{\mu }\dot{\nu }\dot{\lambda }}}}{{\partial }_{\mu }}{{A}_{{\nu \dot{\mu }}}}{{\partial }_{{\dot{\nu }}}}{{A}_{{\lambda \dot{\lambda }}}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2e60523929b3692855ecff6f9f61ea1a_l3.png)

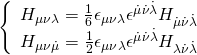

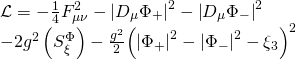

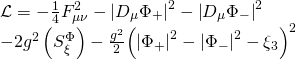
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\exp \left\{ {-\frac{1}{2}} \right.{{\sigma }_{3}}\otimes {{H}^{{1/2}}}{{\Gamma }_{{\kappa ,67}}}\\\left. {\left[ {\left( {{{\theta }_{1}}-{{\theta }_{2}}} \right)\left( {1+{{\Gamma }_{{\kappa ,6789}}}} \right)+\left. {\left( {{{\theta }_{1}}+{{\theta }_{2}}} \right)\left( {1-{{\Gamma }_{{\kappa ,6789}}}} \right)} \right]} \right.} \right\}\\\otimes {{\Gamma }_{{\kappa ,6789}}}{{\epsilon }_{0}}=0\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f2f3b65217a8a22fc2d9e86210982a88_l3.png)
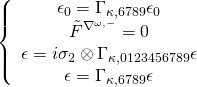
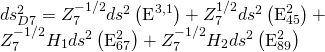
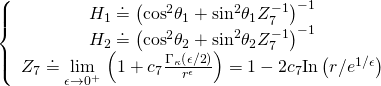
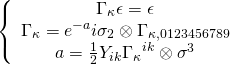
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{e}^{{-\frac{1}{2}{{Y}_{{ik}}}{{\Gamma }_{\kappa }}^{{ik}}\otimes {{\sigma }^{3}}}}}=\frac{1}{{\sqrt{{\left| {\eta +{{{\tilde{F}}}^{{{{{\not{\nabla }}}^{\omega }}}}}} \right|}}}}\left[ {1-\frac{1}{2}{{\sigma }_{3}}{{\Gamma }_{\kappa }}^{{ik}}{{{\tilde{F}}}^{{{{{\not{\nabla }}}^{\omega }}}}}{{\,}_{{ik}}}} \right.\\\left. {+\frac{1}{8}{{\Gamma }_{\kappa }}^{{ikml}}{{{\tilde{F}}}^{{{{{\not{\nabla }}}^{\omega }}}}}{{\,}_{{ik}}}{{{\tilde{F}}}^{{{{{\not{\nabla }}}^{\omega }}}}}{{\,}_{{ml}}}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-13eb91b1609e9ce6d0029ea6b16da3d8_l3.png)