As we saw in my last post, the Standard ΛCDM Model of cosmology can be derived from Type-IIB SUGRA by identifying the inflaton with the Gukov-Vafa-Witten topologically twisted Kähler modulus embedded in a ![]() brane/anti-brane system. The advantages of the
brane/anti-brane system. The advantages of the ![]() system is that we can apriori embed anti-brane instantonic effects to allow de Sitter solutions, and by mirror symmetry, we get a Kaloper-Sorbo axion monodromy inflation, where the flatness of the inflaton potential is protected without dependence on a moduli stabilization mechanism. Noting that
system is that we can apriori embed anti-brane instantonic effects to allow de Sitter solutions, and by mirror symmetry, we get a Kaloper-Sorbo axion monodromy inflation, where the flatness of the inflaton potential is protected without dependence on a moduli stabilization mechanism. Noting that ![]() -branes probing Calabi-Yau 3-folds support 4-D
-branes probing Calabi-Yau 3-folds support 4-D ![]() supersymmetric Yang-Mills gauge theories whose intersection-points generate the Standard Model chiral matter sector and generally the action of a
supersymmetric Yang-Mills gauge theories whose intersection-points generate the Standard Model chiral matter sector and generally the action of a ![]() -brane is given by a Dirac-Born-Infeld part coupled to a Chern-Simons WZ part:
-brane is given by a Dirac-Born-Infeld part coupled to a Chern-Simons WZ part:
![]()
with:
![]()
![]()
where ![]() is the worldvolume pullback with
is the worldvolume pullback with ![]() -orientifold action:
-orientifold action:
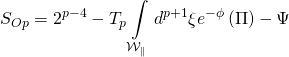
with:
![]()
and
![]()
where the pullback to the ![]() -worldvolume yields the 10-D SYM action:
-worldvolume yields the 10-D SYM action:
![]()
with string coupling:
![]()
and the 10-D SUGRA dimensionally reduced Type-IIB action is:
![]()
with:
![]()
![]()
![]()
and in the string-frame, the type-IIB SUGRA action is given by:
![]()
with:
![]()
![]()
![]()
where the Calabi-Yau superpotential is:
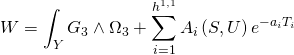
where:
![]()
is the Gukov-Vafa-Witten superpotential stabilization complex term, as well as the axio-dilaton field:
![]()
Given the presence of ![]() -brane instantons,
-brane instantons, ![]() are of Kähler moduli Type-IIB-orbifold class:
are of Kähler moduli Type-IIB-orbifold class:
![]()
with ![]() being the volume of the divisor
being the volume of the divisor ![]() and
and ![]() the 4-form Ramond-Ramond axion field corresponding to:
the 4-form Ramond-Ramond axion field corresponding to:
![]()
and:
![]()
where ![]() is the Kähler form:
is the Kähler form:
![]()
and:
![]()
an integral-form basis and ![]() the associated intersection coefficients. Hence, the Kähler potential is given by:
the associated intersection coefficients. Hence, the Kähler potential is given by:
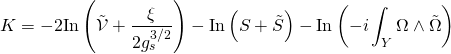
with ![]() the Calabi-Yau volume, and in the Einstein frame, is given by:
the Calabi-Yau volume, and in the Einstein frame, is given by:
![]()
The ![]() -term is given by:
-term is given by:
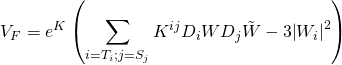
with the Large Volume Scenario ![]() -term is given by:
-term is given by:
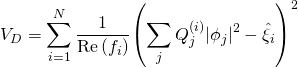
with:
![]()
and the Fayet-Illopoulos terms being:
![]()
where ![]() are the
are the ![]() -brane charge-vectors. Then we saw that the Chern-Simons orientifold action gets a Calabi-Yau curvature correction in the form of:
-brane charge-vectors. Then we saw that the Chern-Simons orientifold action gets a Calabi-Yau curvature correction in the form of:
![Rendered by QuickLaTeX.com \displaystyle {{S}_{{{{O}_{p}},CS}}}=-{{2}^{{p-4}}}-{{T}_{p}}\int\limits_{{{{\mathcal{W}}^{\prime }}}}{{P\left[ C \right]}}\wedge \Theta](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-371c7b529216d796ebd4b8241427e1d1_l3.png)
with
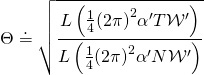
due to the Gauss–Codazzi equations:
![]()
One can and should enhance such a Kähler scenario to one that involves a ![]() -brane inflationary theory mainly due to the fact that in this context, moduli stabilization entails the existence of a
-brane inflationary theory mainly due to the fact that in this context, moduli stabilization entails the existence of a ![]() –
–![]() de Sitter compactification that inherits the Lambda-CDM
de Sitter compactification that inherits the Lambda-CDM ![]() -CP gauge-bundle, yielding a non-truncated N=1 4D SYM on the bulk, deriving inflation on the
-CP gauge-bundle, yielding a non-truncated N=1 4D SYM on the bulk, deriving inflation on the ![]() -manifold orbifolded by the corresponding ALE singularities that give rise to the SM gauge structure and resolutions that yield the Dirac chiral-fermionic SM structure, giving rise to an isomorphism with a
-manifold orbifolded by the corresponding ALE singularities that give rise to the SM gauge structure and resolutions that yield the Dirac chiral-fermionic SM structure, giving rise to an isomorphism with a ![]() Abrikosov-Nielsen-Olesen type manifold. Thus, we can identify the
Abrikosov-Nielsen-Olesen type manifold. Thus, we can identify the ![]() -brane system with an N = 2 gauge theory associated with the D-term inflation model I derived above, but with one hypermultiplet and one Fayet-Iliopoulos term, and dimensionally reduce to N=1. In this, part 1, I will defend such a
-brane system with an N = 2 gauge theory associated with the D-term inflation model I derived above, but with one hypermultiplet and one Fayet-Iliopoulos term, and dimensionally reduce to N=1. In this, part 1, I will defend such a ![]()
![]() –
–![]() de Sitter brane inflationary scenario.
de Sitter brane inflationary scenario.
In a ![]() brane system, a spontaneously broken
brane system, a spontaneously broken ![]() gauge symmetry corresponds to a bound state where the
gauge symmetry corresponds to a bound state where the ![]() dissolves as a deformed Abelian instanton on the
dissolves as a deformed Abelian instanton on the ![]() Dirac-Born-Infeld theory of the
Dirac-Born-Infeld theory of the ![]() brane with Chern-Simons coupling:
brane with Chern-Simons coupling:
![]()
where ![]() gets a background NSNS
gets a background NSNS ![]() as well as
as well as ![]() worldvolume gauge field contributions. Hence, the NSNS two-form becomes a non-commutative deformation parameter in this system. The
worldvolume gauge field contributions. Hence, the NSNS two-form becomes a non-commutative deformation parameter in this system. The ![]() brane system has an unbroken supersymmetry due to a
brane system has an unbroken supersymmetry due to a ![]() -brane
-brane ![]() -symmetry. The vacuum endpoints is describable hence by a non-marginal bound state of
-symmetry. The vacuum endpoints is describable hence by a non-marginal bound state of ![]() and
and ![]() -branes corresponding to the Higgs phase of the gauge theory of the
-branes corresponding to the Higgs phase of the gauge theory of the ![]() -system. The LE-effective action of such a
-system. The LE-effective action of such a ![]() -system in flat space is:
-system in flat space is:
![]()
with:
![]()
![]()
and
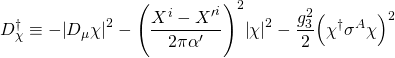
with ![]() the Chern-Simons part, with:
the Chern-Simons part, with:
The doublet arises as the lightest d.o.f from strings stretched between the ![]() -brane and the parallel
-brane and the parallel ![]() -brane, with covariant derivative:
-brane, with covariant derivative:
![]()
and our metric has a Chern-Simons form:
![]()
We now must geometrically locate our system in a background that incorporates the field ![]() and turn on a Ramond-Ramond field-strength
and turn on a Ramond-Ramond field-strength ![]() compatible with the orbifold and orientifold structure of the system with a metric of the form:
compatible with the orbifold and orientifold structure of the system with a metric of the form:
![]()
![]() the 4D metric in the Einstein frame and
the 4D metric in the Einstein frame and ![]() is a section on
is a section on ![]() that factors in moduli stabilization involved in wrapping branes on cycles in the compact space
that factors in moduli stabilization involved in wrapping branes on cycles in the compact space ![]() .
.
Let us analyze the ![]() action. In a curved background given by our metric, this contribution to the LE-effective action:
action. In a curved background given by our metric, this contribution to the LE-effective action:
![]()
reduces to:
![]()
with:
![]()
![]()
![]()
![]()
and we have integrated out the ![]() fluctuation-modes in the
fluctuation-modes in the ![]() directions. The
directions. The ![]() brane covariant 2-form is composed of two terms:
brane covariant 2-form is composed of two terms:
![]()
with ![]() the field strength of the vector field
the field strength of the vector field ![]() living on the brane and
living on the brane and ![]() the pullback of the space-time NS-NS two-form field to the worldvolume of the
the pullback of the space-time NS-NS two-form field to the worldvolume of the ![]() -brane, with a Chern-Simons part induced by the RR field. Now let
-brane, with a Chern-Simons part induced by the RR field. Now let
![]()
be the volume of a fixed ![]() . Integrating over
. Integrating over ![]() gives us:
gives us:
![]()
with:
![]()
![]()
![]()
![]()
![]()
and with coupling constants:
![]()
with our four-form given by:
![]()
thus the ![]() -Chern-Simons term becomes:
-Chern-Simons term becomes:
![]()
with:
![]()
Now since the ![]() invariant 5-form is self-dual in 10-D, there must be a 4-form field in all 10-dimensions. Hence, our action becomes:
invariant 5-form is self-dual in 10-D, there must be a 4-form field in all 10-dimensions. Hence, our action becomes:
![]()
with:
![]()
![]()
![]()
![]()
Adding coincident ![]() -branes forces us to generalize the connection
-branes forces us to generalize the connection ![]() with corresponding Chan-Patton
with corresponding Chan-Patton ![]() gauge fields and a Yukawa-quiver gauge-theory describing the system.
gauge fields and a Yukawa-quiver gauge-theory describing the system.
After embedding the ![]() -brane in the same metric and Ramond-Ramond system, we get the following
-brane in the same metric and Ramond-Ramond system, we get the following ![]() -action:
-action:
![]()
with:
![]()
![]()
![]()
Hence, the ![]() -modified total action is:
-modified total action is:
![]()
with:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
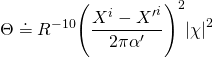
![]()
Note that the hypermultiplet covariant derivative is still of the form:
![]()
hence, we can do the following gauge transformation:
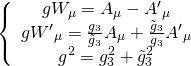
consistent with:
![]()
Thus, our action now has the form:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=\int{{{{d}^{4}}}}x\sqrt{{-{{g}_{E}}}}\left[ {-\frac{1}{4}} \right.{{\left( {{{F}_{W}}} \right)}^{2}}-\frac{1}{4}{{\left( {{{F}_{{{W}'}}}} \right)}^{2}}-\\{{\left| {\partial S} \right|}^{2}}-{{\left| {\partial {S}'} \right|}^{2}}-{{R}^{{-12}}}\frac{1}{{8g_{7}^{2}}}\int_{{K3}}{{{{{\tilde{F}}}^{D}}^{-}\wedge *{{{\tilde{F}}}^{D}}^{-}}}-\\{{\left| {{{D}_{\mu }}\chi } \right|}^{2}}-2{{g}^{2}}{{\left| S \right|}^{2}}{{\left| \chi \right|}^{2}}\left. {-\frac{{\left( {g_{3}^{2}+\tilde{g}_{3}^{2}} \right)}}{2}{{{\left( {{{\chi }^{\dagger }}{{\sigma }^{A}}\chi } \right)}}^{2}}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-daa9b8f3bdc50e63050642e211f74c8f_l3.png)
Our string sectors and all our fields satisfy the required N = 1 chiral superfield-normalization condition and we have rigid N = 2 supersymmetry that gets naturally broken to N = 1 when coupled to gravity in D = 4. In part III of this series, we shall consider M5-brane effects and derive the P-term action.
