Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

The Superstring and the Duality of Topological Strings

By Posted on In Grand Unification Physics, M Theory, Mathematics, Physics, Super String Theory, Witten Theory ,
Duality of Topological Strings

I will finish my analysis of the interconnectedness of string field theory, 4-D space-time and the topological superstring here and derive a crucial duality between topological strings. Aside: the book on the cover is a must-read. I last showed that the bosonic part of the action in the A-model is given as:

    \[\begin{array}{l}I = i\int_\Sigma {dz} \wedge d\bar z{g_{IJ}}{{\not \partial }_z}{\phi ^I}{{\not \partial }_{\bar z}}{\phi ^J} \cdot \\ = 2i\int_\Sigma {dz} \wedge d\bar z{g_{i\overline j }}{{\not \partial }_z}{\phi ^{\bar i}}{{\not \partial }_{\bar z}}{\phi ^j} - \\i\int_\Sigma {dz} \wedge d\bar z{g_{i\overline j }}\left( {{{\not \partial }_z}{\phi ^{\bar i}}{{\not \partial }_{\bar z}}{\phi ^j} - {{\not \partial }_z}{\phi ^j}{{\not \partial }_{\bar z}}{\phi ^{\bar i}}} \right)\\ = 2i\int_\Sigma {dz} \wedge d\bar z{g_{i\overline j }}{{\not \partial }_z}{\phi ^{\bar i}}{{\not \partial }_{\bar z}}{\phi ^j} + \\\int_\Sigma {{\Phi ^ * }} \left( \omega \right)\end{array}\]

where:

    \[I = i\int_\Sigma {dz} \wedge d\bar z{g_{IJ}}{{\not \partial }_z}{\phi ^I}{{\not \partial }_{\bar z}}{\phi ^J}\]

vanishes for the instantons, and so:

    \[S = it\int_\Sigma {{d^2}} z\left\{ {\tilde Q',V} \right\} + t\int_\Sigma {{\Phi ^ * }} \left( {\hat K} \right)\]

reduces to:

    \[S = \frac{1}{2}\int {\left( {{\rm A} * 'Q{\rm A} + {\rm A} * '{\rm A} * '{\rm A}} \right)} \]

due to the following identity:

    \[\int_\Sigma {{\Phi ^ * }} \left( \omega \right) = \int_{\partial \Sigma } {{\Phi ^ * }} \left( \rho \right) = 0\]

Noting that the low lying topological string modes are functions with the form {\rm A}\left( {{q^a},{\chi ^b}} \right) and the fields are linear in \chi, the following expansion is hence valid:

    \[{\rm A} = {\chi ^a}{A_a}\left( q \right)\]

Hence, from

    \[\left\{ {\begin{array}{*{20}{c}}{\omega = d\rho }\\{{g_{i\overline j }} = {g_{j\overline i }} = - {\omega _{i\overline j }}}\end{array}} \right.\]

one can see that in the limit t → ∞, the first part of the string field action is

    \[\frac{1}{2}\int_M {{\rm{Tr}}} A \wedge dA\]

In the cubic analysis context of the action, we saw that for the gauge field mode {A^{\left( j \right)}} of A, the vertex operator is:

    \[{V^{\left( j \right)}} = {\chi ^a}A_a^{\left( j \right)}\left( q \right)\]

Thus, given the superstring SL(2, R) symmetry, one needs only factor in:

    \[\left\langle {{V^{\left( 1 \right)}}\left( 0 \right){V^{\left( 2 \right)}}\left( 1 \right){V^{\left( 3 \right)}}\left( \infty \right)} \right\rangle \]

Then, since the pullback of the Kähler form \hat K is:

    \[\int_\Sigma {{\Phi ^*}} \left( {\hat K} \right)\]

the path integral reduces to an integral over zero modes in the large t limit, and we get

the action for the Chern-Simons gauge theory

    \[\begin{array}{l}S = \frac{1}{2}\int_M {{\rm{Tr}}} \left( {A \wedge dA + \frac{2}{3}A \wedge A \wedge A} \right)\\ = \frac{1}{2}\int_M {{d^3}} q{\rm{Tr}}\left( {{\varepsilon ^{\mu \nu \lambda }}\left( {{A_\mu }{{\not \partial }_\nu }{A_\lambda }} \right) + {A_\mu }{A_\nu }{A_\lambda }} \right)\end{array}\]

In topological string field theory, the path integral reduction, unlike non-topological string theory, is exact, and thus via Feynman path summation we made contact with 4-D space-time physics

Note that the expansion of the {\rm A} field in the A-model is:

    \[{\rm A} = \eta \overline i {A_{\overline i }}\left( {{\phi ^I}} \right)\]

so it follows that the pure physical field is a 1-form typed (0,1) and we have the following gauge-transformational reduction:

    \[\delta {\rm A}:\overrightarrow {{\mathop{\rm Re}\nolimits} d\left| {_{\eta \overline i }} \right.} \delta A\bar \partial \varepsilon \]

Recalling that in the B-model, the (0,2) part of the field strength necessarily vanishes, and that entails that it is coupled to gauge fields.

Thus, the space-time action has the classical solution reflecting that property

So, analogously with the A-model that I discussed here, the action is reduced to:

    \[S = \frac{1}{2}\int_X \Omega \wedge {\rm{Tr}}\left( {A \wedge \bar \partial A + \frac{2}{3}A \wedge A \wedge A} \right)\]

with \Omega a non-zero holomorphic 3-form everywhere-definable.

The superstring

Before deriving the duality of topological strings, let me discuss the superstring. In the closed string superspace section, the target space envelope determines amplitude of the untwisted theory. Since Edward Witten showed in ‘Chern-Simons Gauge Theory as a String Theory‘ that on-shell coupling between the open string and the closed string is zero, topologically, I can work with open string field theory without any loss of generality. In same-said Witten paper, Edward showed that the natural context is type I string-theory. The topological twisting is caused by the gaugino field, denoted here by the operator V_\Psi ^ \pm, which is precisely the spectral flow operator in the internal N = 2 theory acting on the space-time fermionic fields, and so intersects the string world-sheet at ‘curvature singularity’. After factoring the zero modes in the topological cylinder-twisting, we get:

    \[{F_{0,h}} = {\left\langle {{{\left[ {\oint_{{S_i}} {V_\Psi ^ + \oint_{{S_i}} {V_\Psi ^ - } } } \right]}^{h - 2}}\oint_S {{V_F}\oint_S {{V_F}} } } \right\rangle _{{\rm{untwisted}}}}\]

with {S_i} the metaplectic-slits on the twisted cylinder, S is one of the boundaries of the cylinder and {V_F} the gauge field vertex operator.

Hence, we can deduce:

    \[{\rm{Tr}}{F^2}{\left[ {{\rm{Tr}}{\Psi ^2}} \right]^{h - 2}}\]

with the superpotential term:

    \[\int {{d^2}} \theta {\left[ {\left( {{\rm{Tr}}{W^2}} \right)} \right]^{h - 1}}\]

and at higher genus amplitudes, we have:

    \[\int {{d^2}} {\tilde W^{2g}}{\left[ {{\rm{Tr}}{W^2}} \right]^{h - 1}}\]

Hence, from

    \[\int_\Sigma {{\Phi ^ * }} \left( \omega \right) = \int_{\partial \Sigma } {{\Phi ^ * }} \left( \rho \right) = 0\]

we can derive that

the SU(N) Chern-Simons theory on 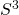{S^3} is exactly dual to the topological closed string on the symplectically resolved conifold, constituting a duality between the topological open string and the topological closed string, since the Chern-Simons gauge theory is realizable as an open string on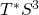 {T^ * }{S^3}

The free energy can be expanded as:

    \[F = \sum {{N^h}} {\kappa ^{E - V}}f\left( {h,E,V} \right)\]

which the ’t Hooft large limit coupling \lambda = \kappa N yields a reduction to:

    \[F = \sum\limits_{g = 0,h = 1}^\infty {{C_{g,h}}} {N^{2 - 2g}}{\lambda ^{2g - 2 + h}}\]

amounting to a perturbative expansion of the open string theory.

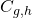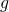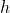hence, that the Chern-Simons gauge theory is equivalent to the open topological string theory entails that {C_{g,h}} is given by the partition function of the open string of the Riemann surface with genus g and h holes, and so we have: the topological open string on 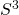{S^3} is equivalent to the topological closed string on the conifold

and this holds since, as I showed, the superstring action satisfies the symmetries of the Seiberg–Witten equation

Untitled43t

 

previously

previously

String Field Theory, 4-D Space-Time and the Superstring
up next

up next

T-Branes and F-Theory: Towards GUT-Model-Construction
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on