The Quantum Master Equation and Supersymmetric-Field-Cosmology

By George Shiber Saturday, September 24, 2016Friday, October 26, 2018 In Cosmology, Grand Unification Physics, Loop Quantum Gravity, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Super String Theory, Supersymmetry cosmology, Loop Quantum Gravity

Supersymmetric-field theory remains the best new physics beyond the SM and also “builds a bridge between the low energy phenomenology and high-energy fundamental physics“. Moreover, I will show here that SuSy can incorporate aspects of loop quantum gravity to shed deep light on fundamental issues in quantum cosmology. Before getting deep, recall that the central action for supersymmetric field theory is:

$\begin{array}{l}{S_0} = \sum\limits_\nu {\int {d\phi } } \left[ {{{\tilde D}^2}} \right.\left\{ {\Omega _i^\dagger } \right.\left( \wp \right)\nabla _a^2{\Omega ^j}\left( \wp \right)\\{\left. {\left. { + \,\omega _i^a\left( \wp \right)\omega _a^i} \right\}} \right]_{\left| {_G} \right.}}\end{array}$

with $\left| {_G} \right.$ the Grassmannian variable and total action is given by:

$\begin{array}{c}{S_T} = {S_0} + \sum\limits_\nu {\int {d\phi } } \left[ {{{\tilde D}^2}} \right.\left\{ {{B_i}} \right.\left( \wp \right){{\tilde D}^a}\Gamma _a^i\left( \wp \right)\\ + \,{{\bar c}_i}\left( \wp \right){{\tilde D}^a}{\nabla _a}{c^i}{\left. {\left. {\left( \wp \right)} \right\}} \right]_{\left| {_G} \right.}}\end{array}$

and the super-field/anti-super-field theory expansion in the Landau type gauge is given by:

$\begin{array}{l}{Z_L}\left[ 0 \right] = \int {\not D} M{e^{ - {W_L}\left[ {\Phi ,{\Phi ^ * }} \right]}} = \\\int {\not DM\exp \left[ { - \left( {{S_0}} \right.} \right.} + \sum\limits_\nu {\int {d\phi } } \left[ {\Gamma _{1i}^{a * }} \right.\\ \cdot {\nabla _a}{c^i} + c_{1i}^ * f_{kj}^i{c^k}{c^j} + \bar c_{1i}^ * \left. {\left. {{{\left. {{B^i}} \right]}_{\left| {_G} \right.}}} \right)} \right]\end{array}$

with the super-covariant derivatives of

$\left\{ {\begin{array}{*{20}{c}}{{\Omega ^i}\left( \wp \right)}\\{{\Omega ^{i\dagger }}\left( \wp \right)}\end{array}} \right.$

are defined by:

${\nabla _a}{\Omega ^i}\left( \wp \right) = {\tilde D_a}{\Omega ^i}\left( \wp \right) - if_{kj}^i\Gamma _a^k\left( \wp \right){\Omega ^j}\left( \wp \right)$

and

${\nabla _a}{\Omega ^{i\dagger }}\left( \wp \right) = {\tilde D_a}{\Omega ^{i\dagger }}\left( \wp \right) - if_{kj}^i{\Omega ^{k\dagger }}\left( \wp \right)\Gamma _a^i\left( \wp \right)$

and the super-derivative is:

${\tilde D_a} = {\not \partial _a} + K_a^b{\theta _b}$

where the Ashtekar-Barbero connection $K_a^i$ , for a, b = 1, 2, 3, is given in terms of co-triads $e_a^i$ :

$K_a^i(x) = {K_{ab}}(x){e^{bi}}(x)$

and $e_a^i$ satisfying

$E_i^a = \left| {\det \left( {e_a^i} \right)} \right|e_a^i(x)$

and the extrinsic curvature ${K_{ab}}$ being:

${K_{ab}} = \frac{1}{{2{N_{lapse}}}}\left( {{{\dot h}_{ab}} - {\nabla _a}N{{_b^{shift}}^\prime } - {\nabla _b}N{{_a^{shift}}^ * }} \right)$

For definitions of terms, see my ‘SuperSymmetric Field Theory and the Quantum Master Equation‘ post. Some philosophical points are in order first.

In this, part 1, I will take the analysis up to but not inclusive of deriving a supersymmetric generalization of group field cosmology and derive the group field cosmology action and the corresponding equation of motion. Aside: I highly recommend this book.

First, although loop quantum gravity is provably not an adequate quantum gravity theory nor a successful unification paradigm, some of its mathematical-physics insights can, via super-group-field theory, shed light, in conjunction with supersymmetric-field-cosmology, on a GUT quantum cosmology theory. LQG theory is background independent quantization of gravity (though not successful) where the Hamiltonian constraint is given via the Ashtekar-Barbero connection and densitized triad mentioned above. Hence, the curvature of the connection is determined by the holonomy around a loop whose corresponding Hilbert space is a space of spin networks and the spin foam arises analytically from the time evolution of these spin networks, implying that it is a second quantized formalism. One, as usual, gets via a third quantization of LQG the corresponding group field theory that is homeomorphic to a quotiented orfibold in supersymmetric field theory. Read this for a great exposition and background for this technical post.

Crucial is to realize that in loop quantum gravity, the holonomies of the connection are given by operators. Given the Ashtekar-Barbero connection, the metric is:

$d{s^2} = - {N^2}\left( t \right)d{t^2} + {a^2}\left( t \right){\delta _{ab}}d{x^a}d{x^b}$

with $a\left( t \right)$ the scalar factor and $N\left( t \right)$ the lapse function discussed in my post here. With the crucial Barbero-Immirzi parameter $\gamma$ and the Levi-Civita connection ${\left( {\omega _0^i} \right)_a}$ , we have:

$A_a^i = \gamma {\left( {\omega _0^i} \right)_a}$

and $A_a^i$ is completely determined in loop quantum cosmology by:

$c = \pm \Upsilon _0^{1/3}{N^ - }\gamma a'$

with $a'$ the time derivative of $a$ . The operators:

$\left\{ {\begin{array}{*{20}{c}}{p = \pm \,{a^2}\Upsilon _0^{1/3}}\\{{e^{i\mu c}}}\end{array}} \right.$

$c$ being the conjugate to $p$ , $\mu$ a function of $p$ . Thus,

$\mu = {\left| p \right|^{ - 1/2}}$

is a basis of the eigenstates of the volume operator 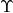$\Upsilon$ and we have

$\Upsilon \left| {{\nu _\Upsilon }} \right\rangle = 2\pi \gamma G\left| {{\nu _\Upsilon }} \right|\left| {{\nu _\Upsilon }} \right\rangle$

with the dimensions of length being

${\nu _\Upsilon } = \pm \,{a^2}{\Upsilon _0}/2\pi \gamma G$

Now, the curvature of $A_a^i$ is given via the holonomy around a loop and the area of such a loop cannot be smaller than a fixed minimum area since the smallest eigenvalue of the area operator in loop quantum gravity is nonzero! Hence, in Planck units, the Hamiltonian constraint for a homogeneous isotropic universe with a massless scalar field $\phi$ is given as:

${K^2}\Phi \left( {{\nu _\Upsilon },\phi } \right) = \left[ {{E^2} - \not \partial _\phi ^2} \right]\Phi \left( {{\nu _\Upsilon },\phi } \right) = 0$

where ${E^2}$ is defined as:

$\begin{array}{l}{E^2}\Phi \left( {{\nu _\Upsilon },\phi } \right) = - {\left[ {B\left( {{\nu _\Upsilon }} \right)} \right]^{ - 1}}{C^ + }\left( {{\nu _\Upsilon }} \right)\\\Phi \left( {{\nu _\Upsilon } + 4,\phi } \right) - {\left[ {B\left( {{\nu _\Upsilon }} \right)} \right]^{ - 1}}{C^0}\left( {{\nu _\Upsilon }} \right)\Phi \left( {{\nu _\Upsilon },\phi } \right)\\ - {\left[ {B\left( {{\nu _\Upsilon }} \right)} \right]^{ - 1}}{C^ - }\left( {{\nu _\Upsilon }} \right)\Phi \left( {{\nu _\Upsilon },\phi } \right)\end{array}$

with ${\nu _\Upsilon } = 4$ and for the gauge-choice in loop quantum cosmology, we have as usual:

${C^ - }\left( {{\nu _\Upsilon }} \right) = {C^ + }\left( {{\nu _\Upsilon } - 4} \right)$

Setting $N = 1$ , the canonical quantization scheme yields:

${C^ + }\left( {{\nu _\Upsilon }} \right) = \frac{1}{{12\gamma \sqrt {2\sqrt 3 } }}\left| {{\nu _\Upsilon } + 2} \right|\left| {{\nu _\Upsilon } + 1} \right| - \left| {{\nu _\Upsilon } + 3} \right|$

${C^0}\left( {{\nu _\Upsilon }} \right) = - {C^ + }\left( {{\nu _\Upsilon }} \right) - {C^ + }\left( {{\nu _\Upsilon } - 4} \right)$

$B\left( {{\nu _\Upsilon }} \right) = \frac{{3\sqrt 2 }}{{8\sqrt {\sqrt 3 \pi \gamma G} }}\left| {{\nu _\Upsilon }} \right|{\left| {{{\left| {{\nu _\Upsilon } + 1} \right|}^{1/3}} - {{\left| {{\nu _\Upsilon } + 1} \right|}^{1/3}}} \right|^3}$

and with $N = {a^3}$ , solvably, we have:

$\left\{ {\begin{array}{*{20}{c}}{{C^ + }\left( {{\nu _\Upsilon }} \right) = \frac{{\sqrt 3 }}{{8\gamma }}\left( {{\nu _\Upsilon } + 2} \right)}\\{{C^0}\left( {{\nu _\Upsilon }} \right) = \frac{{\sqrt 3 }}{{4\gamma }}{\nu _\Upsilon }}\\{B\left( {{\nu _\Upsilon }} \right) = \frac{1}{{{\nu _\Upsilon }}}}\end{array}} \right.$

and philosophically deep, as it is a fatal flaw, though not for the purposes of our analysis, the matter variable appears as the time variable in loop quantum cosmology

Generally, since a wave-function of an n-th quantized theory is a classical field in an n+1 quantized formalism, the wave function of loop quantum cosmology is a classical field of group field cosmology with bosonic field theory action:

${S_{bos}} = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi \,\Phi } } \left( {{\nu _\Upsilon },\phi } \right){K^2}\Phi \left( {{\nu _\Upsilon },\phi } \right)$

with expansion:

$\Phi \left( {b,\phi } \right) = \sum\limits_{{\nu _\Upsilon }} \Phi \left( {{\nu _\Upsilon },\phi } \right){e^{i{\nu _\Upsilon }b}}$

$\Phi \left( {{\nu _\Upsilon },\phi } \right) = \int_0^{\pi /2} {db} \,\Phi \left( {b,\phi } \right){e^{ - i{\nu _\Upsilon }b}}$

Thus, the bosonic action reduces to:

${S_{bos}} = \frac{1}{\pi }\int {d\phi } \int {db\,} \bar \Phi \left( {b,\phi } \right){\tilde K^2}\Phi \left( {b,\phi } \right)$

When the fields are promoted to operators, one can define the Fock space by the action of creation operators on a vacuum state that is defined as annihilated by all annihilation operators ${a_k}\left| 0 \right\rangle = 0$ , and each operator can create or annihilate universes, and so we have a representation of a process of splitting of/joining of universes. Since bosonic states/statistics are not sufficient to determine the full Fock space, fermionic states/statistics must be integrated. In parallel with a fermionic field in two dimensions, one defines a fermionic field in group field cosmology via:

${\Psi _a}\left( {{\nu _\Upsilon },\phi } \right) = \left( {{\Psi _1}\left( {{\nu _\Upsilon },\phi } \right),{\Psi _2}\left( {{\nu _\Upsilon },\phi } \right)} \right)$

with spinor indices raised/lowered by the second-rank antisymmetric tensors ${C^{ab}}$ , ${C_{ab}}$ :

${\Psi ^a}\left( {{\nu _\Upsilon },\phi } \right) = {C^{ab}}{\Psi _b}\left( {{\nu _\Upsilon },\phi } \right)$

${\Psi _a}\left( {{\nu _\Upsilon },\phi } \right) = {\Psi ^b}\left( {{\nu _\Upsilon },\phi } \right){C_{ba}}$

where the 2-nd-RAST satisfies:

${C_{ab}}{C^{cb}} = \delta _a^c$

Now defining:

$\left\{ {\begin{array}{*{20}{c}}{{K_\mu } = \left( {E,{{\not \partial }_\phi }} \right)}\\{{\eta ^{\mu \nu }} = \left( {1, - 1} \right)}\end{array}} \right.$

with ${K_\mu }$ ‘s action is analogous to ${\not \partial _\mu }$ of a ordinary two dimensional field theory, hence, since the following hold:

$\left\{ {\begin{array}{*{20}{c}}{{{\not \partial }_{ab}} = {{\left( {{\gamma ^\mu }{{\not \partial }_\mu }} \right)}_{ab}}}\\{{{\not \partial }^2} = {{\not \partial }^{ab}}{{\not \partial }_{ab}}/2}\end{array}} \right.$

one can define:

${K_{ab}} = {\left( {{\gamma ^\mu }} \right)_{ab}}{K_\mu }$

as well as:

$\begin{array}{c}{K^2} = \frac{1}{2}{K^{ab}}{K_{ab}}\\ = \frac{1}{2}{\left( {{\gamma ^\mu }} \right)^{ab}}{K_\mu }{\left( {{\gamma ^\nu }} \right)_{ab}}{K_\nu }\\ = {\eta ^{\mu \nu }}{K_\mu }{K_\mu }\\ = \left[ {{E^2} - \not \partial _\phi ^2} \right]\end{array}$

with:

$\left\{ {{\gamma ^\mu },{\gamma ^\nu }} \right\} = 2{\eta ^{\mu \nu }}$

Therefore, the fermionic group field cosmology action can be written as:

$\begin{array}{l}{S_f} = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } \,{C^{bc}}{\Psi _c}\left( {{\nu _\Upsilon },\phi } \right)\left( {{\gamma ^\mu }} \right){K_\mu }{\Psi _a}\left( {{\nu _\Upsilon },\phi } \right)\\ = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } \,{\Psi ^b}\left( {{\nu _\Upsilon },\phi } \right)K_b^a{\Psi _a}\left( {{\nu _\Upsilon },\phi } \right)\end{array}$

taking full use of the structural form of solutions to the quantum master equation:

$\left\{ {\begin{array}{*{20}{c}}{\Delta {e^{i{W_\Psi }\left[ {\Phi ,{\Phi ^ * }} \right]}} = 0}\\{\Delta \equiv {{\left( { - 1} \right)}^\varepsilon }\frac{{{{\not \partial }_l}}}{{\not \partial \Phi }}\frac{{{{\not \partial }_l}}}{{\not \partial {\Psi ^ * }}}}\end{array}} \right.$

which have the form:

${W_\Psi }\left[ {\Phi ,{\Phi ^ * }} \right] \equiv \left( {{W_{NL}},{W_L}} \right)$

We are now in a position to establish a map between the two generating functionals corresponding to the above extended actions by use of the superfield/super-antifield dependent BRST transformations

The superfield/super-antifield dependent BRST transformation yields the following Jacobian functional measure:

$\begin{array}{l}{{Z'}_L}\left[ 0 \right] = \int {\not D} M\left( {s{\rm{Det}}J\left[ {\Phi ,{\Phi ^ * }} \right]} \right) \cdot \\\exp \left\{ { - {W_L}\left[ {\Phi ,{\Phi ^ * }} \right]} \right\} = \\\int {\not D} M{e^{ - \left( {{W_L}\left[ {\Phi ,{\Phi ^ * }} \right] - is{\rm{Tr}}\,{\rm{In}}J\left[ {\Phi ,{\Phi ^ * }} \right]} \right)}}\end{array}$

with ${Z'_L}$ referring to the Jacobian change of variables. The associated matrix for the superfield/super-antifield dependent BRST transformation is therefore:

Now, by BRST-nilpotency, we get a reduction to:

$s{\rm{Det}}J\left[ {\Phi ,{\Phi ^ * }} \right] = \frac{1}{{1 + {s_b}}}\Lambda \left[ {\Phi ,{\Phi ^ * }} \right]$

thus simplifying our Jacobian functional measure:

$\begin{array}{c}{{Z'}_L}\left[ 0 \right] = \int {\not D\Phi \exp } \left( { - {W_L}} \right.\left[ {\Phi ,{\Phi ^ * }} \right]\\ - i{\rm{In}}\left. {\left( {1 + {s_b}\Lambda \left[ {\Phi ,{\Phi ^ * }} \right]} \right)} \right)\end{array}$

Hence, the Slavnov variation yields:

$\begin{array}{c}{s_b}\Lambda \left[ {\Phi ,{\Phi ^ * }} \right] = \sum\limits_\nu {\int {d\phi \exp \left( { - i} \right.} } \\\left[ {c_{2i}^ * \left( \wp \right)\left( {\frac{1}{2}f_{kj}^i{c^k}\left( \wp \right){c^j}\left( \wp \right)} \right)} \right. + \\\left( {\bar c_{2i}^ * \left( \wp \right) - \bar c_{1i}^ * \left( \wp \right)} \right){\left. {\left. {{B^i}\left( \wp \right)} \right]} \right)_{\left| {_G} \right.}} - 1\end{array}$

therefore, by Jacobian change of variables and BRST-nilpotency, we get our all too important map

${Z'_L}\left[ 0 \right] = {Z_{NL}}\left[ 0 \right]$

allowing us to derive the equation of motion:

$K_a^b{\Psi _b}\left( {{\nu _\Upsilon },\phi } \right) = 0$

In part 2, I will deduce the supersymmetric generalization of group field cosmology and conclude with some deep results pertaining to gauge symmetry.

1 Response

Supersymmetric Group Field Cosmology and Loop Quantum Gravity
Saturday, October 1, 2016

[…] I showed that the curvature of the Ashtekar-Barbero connection of loop quantum gravity is determined by the holonomy around a loop whose corresponding Hilbert space is a space of spin networks, and that the spin foam arises from the time evolution of these spin networks, implying that it is a second quantized formalism. One then gets via a third quantization of LQG the corresponding group field theory that is homeomorphic to a quotiented orfibold in supersymmetric field theory and thus the wave-function of loop quantum cosmology is a classical field of group field cosmology with bosonic field theory action: […]