I showed that the curvature of the Ashtekar-Barbero connection of loop quantum gravity is determined by the holonomy around a loop whose corresponding Hilbert space is a space of spin networks, and that the spin foam arises from the time evolution of these spin networks, implying that it is a second quantized formalism. One then gets via a third quantization of LQG the corresponding group field theory that is homeomorphic to a quotiented orfibold in supersymmetric field theory and thus the wave-function of loop quantum cosmology is a classical field of group field cosmology with bosonic field theory action:
![]()
with expansion:
![]()
![]()
Hence, the bosonic action reduces to:
![]()
and I wrote the fermionic group field cosmology action:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_f} = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } \,{C^{bc}}{\Psi _c}\left( {{\nu _\Upsilon },\phi } \right)\left( {{\gamma ^\mu }} \right){K_\mu }{\Psi _a}\left( {{\nu _\Upsilon },\phi } \right)\\ = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } \,{\Psi ^b}\left( {{\nu _\Upsilon },\phi } \right)K_b^a{\Psi _a}\left( {{\nu _\Upsilon },\phi } \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-150dd818da1e5fa5a121f241c4ce0284_l3.png)
Then, taking full use of the structural form of solutions to the quantum master equation:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\Delta {e^{i{W_\Psi }\left[ {\Phi ,{\Phi ^ * }} \right]}} = 0}\\{\Delta \equiv {{\left( { - 1} \right)}^\varepsilon }\frac{{{{\not \partial }_l}}}{{\not \partial \Phi }}\frac{{{{\not \partial }_l}}}{{\not \partial {\Psi ^ * }}}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-600fb756a251fa12f05d0c8578d18a73_l3.png)
I derived the form:
![]()
where the superfield/super-antifield dependent BRST transformation yields the Jacobian functional measure:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{{Z'}_L}\left[ 0 \right] = \int {\not D} M\left( {s{\rm{Det}}J\left[ {\Phi ,{\Phi ^ * }} \right]} \right) \cdot \\\exp \left\{ { - {W_L}\left[ {\Phi ,{\Phi ^ * }} \right]} \right\} = \\\int {\not D} M{e^{ - \left( {{W_L}\left[ {\Phi ,{\Phi ^ * }} \right] - is{\rm{Tr}}\,{\rm{In}}J\left[ {\Phi ,{\Phi ^ * }} \right]} \right)}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6f5f81c0ab5908305a7f5e7117d4280b_l3.png)
which allowed us to derive the SSFT-equation of motion:
![]()
I must generate a super-group field theory whose kinetic parts of its bosonic and fermionic component fields determine the Hamiltonian constraint of loop quantum gravity theory. Let ![]() be 2-component anti-commuting parameters with odd Grassmann parity such that:
be 2-component anti-commuting parameters with odd Grassmann parity such that:
![]()
and define the generators of N = 1 supersymmetry via:
![]()
The only covariant derivative that commutes with this generator of supersymmetry is:
![]()
with:
![]()
therefore determining the full D/Q supersymmetric algebra:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\left\{ {{Q_a},{Q_b}} \right\} = \left( {{{\not \partial }_a} - K_a^c{\theta _c}} \right)\left( {{{\not \partial }_b} - K_b^d{\theta _d}} \right)\\ + \left( {{{\not \partial }_b} - K_b^d{\theta _d}} \right)\left( {{{\not \partial }_a} - K_a^c{\theta _c}} \right) = 2{K_{ab}}\\\left\{ {{Q_a},{{\not D}_b}} \right\} = \left( {{{\not \partial }_a} - K_b^c{\theta _c}} \right)\left( {{{\not \partial }_b} - K_b^d{\theta _d}} \right)\\ = - 2{K_{ab}}\\\left\{ {{Q_a},{{\not D}_b}} \right\}\left( {{{\not \partial }_a} - K_a^c{\theta _c}} \right)\left( {{{\not \partial }_b} - K_b^d{\theta _d}} \right)\\ + \left( {{{\not \partial }_b} - K_b^d{\theta _d}} \right)\left( {{{\not \partial }_a} - K_a^c{\theta _c}} \right) = 0\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6ce57afcb7e2f4adb52b1a593d462b55_l3.png)
and the reason that this constitutes an algebra is due to the fact that the following holds:
![]()
I can write down now a supersymmetric theory in the N = 1 superspace formalism with manifest N = 1 supersymmetry in the following way:
Let
![]()
be the superfield defined by:
![]()
Hence, we now have:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\Phi \left( {{\nu _\Upsilon },\phi } \right) = {{\left[ {\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right]}_{\left| {_{{\theta _a} = 0}} \right.}}}\\{{\Psi _a}\left( {{\nu _\Upsilon },\phi } \right) = {{\left[ {{{\not D}_a}\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right]}_{\left| {_{{\theta _a} = 0}} \right.}}}\\{F\left( {{\nu _\Upsilon },\phi } \right) = {{\left[ {{{\not D}^2}\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right]}_{\left| {_{{\theta _a} = 0}} \right.}}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e91a909623ed7a08a15e96b9598ee1ba_l3.png)
The supersymmetric transformations ![]() generated by
generated by ![]() can be derived now in analogy with the regular supersymmetric theory:
can be derived now in analogy with the regular supersymmetric theory:
![]()
![]()
and
![]()
and such supersymmetric transformations are holonomically equivalent to the regular N = 1 transformations in three dimensions with the spacetime replaced by 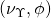 and
and 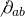 by
by 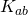
Thus, a superfield theory in this N = 1 superspace can be constructed now
Since N = 1 supersymmetry in three dimensions corresponds to N = 2 supersymmetry in two dimensions, we can use the projection
![]()
to split the super-charge ![]() as:
as:
![]()
which yields an N = 2 supersymmetric theory by dimensional reduction, and the action is:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_s} = \frac{1}{2}\sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } {\left[ {{{\not D}^2}\left[ {\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right]} \right]_{\left| {_{{\theta _a} = 0}} \right.}}\\ = \frac{1}{2}\sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } \left[ {{{\not D}^2}\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right){{\not D}^2}\left( {{\nu _\Upsilon },\phi ,\theta } \right) + } \right.\\{{\not D}^a}\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right){{\not D}_a}{{\not D}^2}\left( {{\nu _\Upsilon },\phi ,\theta } \right) + \\\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right){\left( {{{\not D}^2}} \right)^2}{\left. {\left. {\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right]} \right]_{\left| {_{{\theta _a} = 0}} \right.}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d426da543137a7e716beb7df60e4b01f_l3.png)
which is the necessary and sufficient supersymmetric field model whose bosonic and fermionic parts generate the bosonic and fermionic models of loop quantum cosmology
Adding interactions, we get:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_{si}} = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } {\left[ {{{\not D}^2}\left[ {f\left( {\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right)} \right]} \right]_{\left| {_{{\theta _a} = 0}} \right.}}\\ = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi } \left[ {f''\left( {\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right){{\not D}^a}\Omega {{\left( {\left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right)}^2}} \right.} \\ + f'\left( {\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right){\left. {{{\not D}^2}\Omega \left( {{\nu _\Upsilon },\phi ,\theta } \right)} \right]_{\left| {_{{\theta _a} = 0}} \right.}}\\ = \sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } {\left[ {f''\left( \Phi \right)\left( {{\nu _\Upsilon },\phi } \right){\Psi ^2}\left( {{\nu _\Upsilon },\phi } \right) + f'\left( \Phi \right)\left( {{\nu _\Upsilon },\phi } \right)F\left( {{\nu _\Upsilon },\phi } \right)} \right]_{\left| {_{Grass}} \right.}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-457e639f2658bf43a023f726db81feb1_l3.png)
where we have that
![]()
is the interaction term containing polynomials in both:
![]()
Hence, the superspace interaction term is given by:
![]()
which generates the interaction-component action:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_t} = \frac{1}{2}\sum\limits_{{\nu _\Upsilon }} {\int {d\phi } } \left[ {{F^2}} \right.\left( {{\nu _\Upsilon },\phi } \right) + {\Psi ^b}\left( {{\nu _\Upsilon },\phi } \right)K_b^a\left( {{\nu _\Upsilon },\phi } \right)\\ + \Phi \left( {{\nu _\Upsilon },\phi } \right){K^2}\left( {{\nu _\Upsilon },\phi } \right) + 2\lambda \Phi \left( {{\nu _\Upsilon },\phi } \right){\Psi ^2}\left( {{\nu _\Upsilon },\phi } \right)\\ + \lambda {\Phi ^2}\left( {{\nu _\Upsilon },\phi } \right)\left. {F\left( {{\nu _\Upsilon },\phi } \right)} \right]\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ebb9a0d264a37e20b7c46be5331236b1_l3.png)
with:
![]()
and noting that the structure of the group field cosmology has an effect on the way individual universes interact in the multiverse. So in summation, we have generated the Hamiltonian constraint of loop quantum cosmology from supersymmetric group field cosmology in N = 1 superspace formalism with gauge symmetry, where the component fields of this supersymmetric gauge theory satisfy the Hamiltonian constraint of loop quantum cosmology. In supersymmetric group field cosmology, two real universes interact by an exchange of virtual universes, and the big bang in this model is interpreted as a creation of a pair of universes by the interaction of two other universes via the exchange of a third quantized virtual gauge universe satisfying the third quantized BRST of the supersymmetric group field theory with gauge symmetry: supersymmetrizing the theory takes place at the level of third quantized fields. Thus, in our model, the N = 1 superspace formalism implies that string theory can be interpreted as two dimensional gravity coupled to matter fields quantized via loop quantum gravity. This is crucial, and great progress, as we shall see upon further study.



