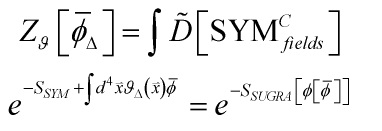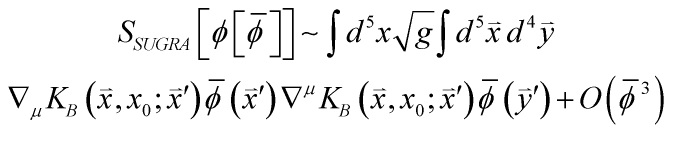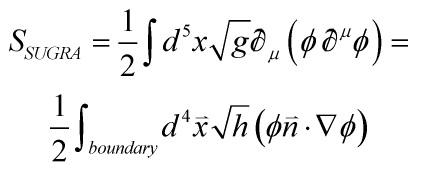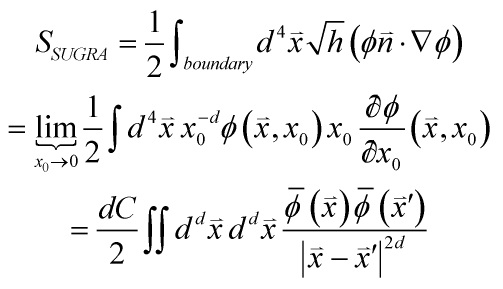The equivalence between string-theory on ![]() -space and 4-D N = 4 super-Yang–Mills conformal field theory is one of the deepest equivalences in physics, mainly due to the fact that the gauge theory lives on the worldvolume of a stack of D3-branes, which is equivalent to living on the boundary of
-space and 4-D N = 4 super-Yang–Mills conformal field theory is one of the deepest equivalences in physics, mainly due to the fact that the gauge theory lives on the worldvolume of a stack of D3-branes, which is equivalent to living on the boundary of ![]() . Throat holographic decoupling is hence essential for extracting the right bulk geometry and boundary topology and that decoupling is mediated by the Witten prescription AdS/CFT-mapping:
. Throat holographic decoupling is hence essential for extracting the right bulk geometry and boundary topology and that decoupling is mediated by the Witten prescription AdS/CFT-mapping:
And that is what I will expand upon here. This is an excellent introduction to super-Yang–Mills conformal field theory. But first, here is a schematic representation of the AdS/CFT duality:
![Rendered by QuickLaTeX.com \[{\left\langle {T\left\{ {\exp \left( {\int {{d^d}x\,{J_{4D}}(x)\vartheta (x)} } \right)} \right\}} \right\rangle _{CFT}} = {\not Z_{AdS}}\left[ {\underbrace {\lim }_{boundary}J\,{w^{\Delta - d + k}} = {J_{4D}}} \right]\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-cdc5fdbdaac4c4ed2505d0082672de8e_l3.png)
or more informatively:
![]()
where ![]() is the ‘bulk-field‘,
is the ‘bulk-field‘, ![]() the radial coordinate that is dual to the renormalization group in the boundary theory, with:
the radial coordinate that is dual to the renormalization group in the boundary theory, with:
![]()
and ![]() in the CFT boundary of AdS with
in the CFT boundary of AdS with ![]() coupled to
coupled to ![]()
The left-hand-sides are the vacuum expectation value of the time-ordered exponential of the operators over CFT; the right-hand-sides are the quantum gravity generating functional with the given conformal boundary condition. So, on one side, we have a gauge theory in flat space-time at weak coupling and as the coupling increases, the theory must be described as a string-theory in curved space-time. Moreover, at really strong coupling, gravity can only be interpreted as a Sasaki-Einstein holographic emergent property. Lately and increasingly, in the AdS/CFT setting, the relation of the original theory without gravity and the one with gravity is best, and it looks only, describable in the context of non-commutative (NC) quantum field theory. There are many important reasons to have non-commutativity. Here are three central ones. One, a quantum theory of gravity in the NC setting needs no renormalizability. Second, at the Planck scale, the graviton can be Picard-Lefschetz ‘localized’ even in light of the energy-time Heisenberg uncertainty relation. And thirdly, NC quantum field theories are now necessary in string-theory: one can actually prove that the dynamics of a D-brane in the presence of anti-symmetric fields can only be described in terms of a Moyal-product deformed gauge theory: hence non-commutativity! Given all that, the Seiberg-Witten map is crucial, since it takes one from a commutative gauge field to a non-commutative one, and the effect of such a map gives rise to the NC-parameter ![]() on matter background fields and induces the interactions that are metaplectically quasimorphic to gravity, where
on matter background fields and induces the interactions that are metaplectically quasimorphic to gravity, where ![]() is the Poisson tensor and the Moyal product
is the Poisson tensor and the Moyal product ![]() :
:
![]()
with:
![]()
holding.
It is well know that the Heisenberg modes of strings in the horizon geometry stay stuck in the throat and are gravitationally bound to the branes whose backreaction sources are the ![]() spacetime,
spacetime,
hence the 10-D flat space SUGRA decouples and isolates the Einstein-Sasaki degrees of freedom.
I will define the bulk-to-boundary propagator:
![]()
with ![]() the
the ![]() -Laplacian, with the RHS representing a delta string-theory source on the boundary of AdS space. And from a bulk solution:
-Laplacian, with the RHS representing a delta string-theory source on the boundary of AdS space. And from a bulk solution:
![]()
one gets the 5-D supergravity action:
Now, by the above 5-D supergravity action and
![]()
we get the following:
![]()
and given that all terms include more than one field ![]() , I can now derive:
, I can now derive:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\left\langle {\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)} \right\rangle = \frac{\delta }{{\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)}}\left( { - \frac{{\delta {S_{SUGRA}}}}{{\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)}}{e^{ - {S_{SUGRA}}}}} \right)\left| {_{\bar \phi = 0}} \right. = \\ - \frac{{{\delta ^2}{S_{SUGRA}}}}{{\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)}}\left| {_{\bar \phi = 0}} \right.\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-88be83f2d6b30eadb821aff1673423a8_l3.png)
I am in a position to consider a free massless scalar field with equation of motion
![]()
with string-theory action:
![]()
Now, the above equation of motion kills one of the field-terms and integrating-by-parts yields the following B-action:
where ![]() is the boundary-metric, and
is the boundary-metric, and ![]() the component of the gradient normal to the boundary.
the component of the gradient normal to the boundary.
Let me unpack now the RHS of the B-action and then take the boundary-limit to zero
Note first that the boundary is defined by a slice of constant ![]() from the B-action, which is an instrinsic part of any string-theory on any AdS-space. Therefore, we have:
from the B-action, which is an instrinsic part of any string-theory on any AdS-space. Therefore, we have:
![]()
and so at the boundary, we have:
![]()
Thus, by the Witten prescription AdS/CFT-mapping and the full bulk solution above, we can derive:
![]()
and from the B-action above, we get:
![Rendered by QuickLaTeX.com \[\frac{{\not \partial {K_B}}}{{\not \partial {x_0}}}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0};\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right) = \frac{{dCx_0^{d - 1}}}{{{{\left( {x_0^2 + {{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^2}} \right)}^d}}} - \frac{{dC2x_0^{d + 1}}}{{{{\left( {x_0^2 + {{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^2}} \right)}^{d + 1}}}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ab15511a1feba0ead4258edfe71d6b66_l3.png)
The denominators in the above, in the limit ![]() , become negligible and crucially:
, become negligible and crucially:
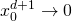 is faster than
is faster than 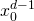
Therefore, the first term dominates yielding:
![Rendered by QuickLaTeX.com \[{x_0}\frac{{\not \partial {K_B}}}{{\not \partial {x_0}}}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0};\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right){ \to _{{x_0} \to 0}}\frac{{dCx_0^d}}{{{{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^{2d}}}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bc34eef4283404b7877dbcfddbcac381_l3.png)
so, I can use:
![]()
to derive the 2-point correlator of the Witten prescription AdS/CFT-mapping:
hence, the 2-point ‘Witten prescription AdS/CFT-mapping‘ function is:
![Rendered by QuickLaTeX.com \[\left\langle {\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)} \right\rangle = \frac{{Cd}}{2}\frac{1}{{{{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^{2d}}}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-31610d8d7bfacffdd40a1977e3c588b9_l3.png)
which is a 2-point correlation function of scalar operators of dimension ![]() in a CFT and is equivalent to a CFT-correlation function from classical supergravity. Using the equivalence between string-theory on
in a CFT and is equivalent to a CFT-correlation function from classical supergravity. Using the equivalence between string-theory on ![]() -space and 4-D N = 4 super-Yang–Mills conformal field theory, the AdS/CFT duality, in light of the Witten prescription AdS/CFT-mapping:
-space and 4-D N = 4 super-Yang–Mills conformal field theory, the AdS/CFT duality, in light of the Witten prescription AdS/CFT-mapping:
yields the desired throat holographic decoupling for the conformal-invariance of 4-D N = 4 super-Yang–Mills field theory in light of that equivalence.