String-Theory and the String/Non-Local-‘Particles’ Duality

By George Shiber Monday, July 25, 2016Saturday, August 17, 2019 In Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Philosophy Of Science, Physics, Super String Theory, Supersymmetry Conformal Symmetry, Elementary Particles Ontology

One of the deepest result in quantum physics is that the Wave-Particle-Duality-Relations correspond to a modern formulation of the Heisenberg uncertainty principle stated in terms of entanglement entropies: a Bell-type argument in the context of T-duality’s winding modes, shows the action describing any particle implies an ontological non-locality intrinsic to the notion of ‘particle’ and in this series of posts, I will show how that entails that ‘non-local-particles‘ (Pages 51-67) can be symmetrically identified with strings in string-theory. Consider, as I showed, the non-commutative action for the dynamics of N-branes of type $J$ in the string regime:

with the D-1-action:

$S_1^D = {\mkern 1mu} - {T_1}\int\limits_{{\rm{worldvolumes}}} {{d^{1 + 1}}} \xi \frac{{\not D_{\mu \nu }^{susy}L}}{{{{\not \partial }_{{v_a}}}}}{e^{ - {\Phi _{bos}}}}{\rm{de}}{{\rm{t}}^{1/2}}G_{ab}^{\exp \left( {H_{1 + 1}^{{\rm{array}}}} \right)}$

and we get from:

${e^{ - {\Phi _{bos}}}}{\rm{de}}{{\rm{t}}^{1/2}}G_{ab}^{\exp \left( {H_{1 + 1}^{{\rm{array}}}} \right)}$

the d-1 mass-term:

${T_1}{e^{ - {\Phi _{bos}}}}\prod\limits_{i = 1}^1 {\left( {2\pi nR} \right)}$

noting that generalizations to fields and D/p-branes are straightforward. In this, part one, I will draw a summary showing that non-local particle-theory with conformal symmetry is characterized by its spectrum $\not Z'$ in string-theory.

Nonlocal actions of particles derived via Feynman integral decomposition on a conformal hypersurface with conformal symmetry gives us a Virasoro algebra as guaranteed by Noether’s theorem

Let us look at what string-theory says about their canonical quantization

Consider quadratic actions of the form:

${S^q} = - \int {dt} x\left( t \right)f\left( {{{\not \partial }_t}} \right)y\left( t \right)$

with scalar fields $x$ and $y$ . A canonical quantization yields the variational action:

$\begin{array}{l}\delta {S^q} = \int {dt\left\{ {\delta x\left[ {f\left( {{{\not \partial }_t}} \right)y\left( t \right)} \right]} \right.} + \\\delta y\left( t \right)\left[ {f\left( { - {{\not \partial }_t}} \right)x\left( t \right)} \right] + x\left( t \right)\left[ {f\left( {{{\not \partial }_t}} \right)\delta y\left( t \right)} \right] - \\\left. {\left[ {f\left( { - {{\not \partial }_t}} \right)x\left( t \right)} \right]\delta y\left( t \right)} \right\}\end{array}$

with equations of motion:

$\left\{ {\begin{array}{*{20}{c}}{f\left( { - {{\not \partial }_t}} \right)x\left( t \right) = 0}\\{f\left( {{{\not \partial }_t}} \right)y\left( t \right) = 0}\end{array}} \right.$

Solving for $x$ and $y$ gives the following solutions:

$x\left( t \right) = \sum\limits_a {{x_a}\,} {e^{ - i{k_a}t}}$

and

$y\left( t \right) = \sum\limits_a {{y_a}\,} {e^{ - i{k_a}t}}$

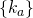with $\left\{ {{k_a}} \right\}$ being the set of zeros of $f$ :

$\not {\rm Z}' = \left\{ {{k_a}} \right\} = \left\{ {k\left| {f\left( {ik} \right) = 0} \right.} \right\}$

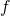Thus, the total derivative of

is:

$\begin{array}{c}x\left( t \right)\left[ {f\left( {{{\not \partial }_t}} \right)\delta y\left( t \right)} \right] - \left[ {f\left( { - {{\not \partial }_t}} \right)x\left( t \right)} \right]\delta y\left( t \right)\\ = \frac{d}{{dt}}\theta \end{array}$

where $\theta$ is:

$\theta = \bullet \left( {\frac{{1 \otimes f\left( {{{\not \partial }_t}} \right) - f\left( { - {{\not \partial }_t}} \right) \otimes 1}}{{1 \otimes {{\not \partial }_t} + {{\not \partial }_t} \otimes 1}}} \right)\left( {x\left( t \right) \otimes \delta y\left( t \right)} \right)$

with

$\bullet \left( {f \otimes g} \right) \equiv fg$

So we get a Taylor expansion:

$f\left( {{{\not \partial }_t}} \right) = \sum\limits_{n = 0}^\infty {{f_n}} \not \partial _t^n$

with the sympletic two-form

$\omega = \delta \theta$

being:

$\begin{array}{l}\omega = \bullet \left( {\frac{{1 \otimes f\left( {{{\not \partial }_t}} \right) - f\left( { - {{\not \partial }_t}} \right) \otimes 1}}{{1 \otimes {{\not \partial }_t} + {{\not \partial }_t} \otimes 1}}} \right)\left( {x\left( t \right) \otimes \delta y\left( t \right)} \right)\\ = \sum\limits_{n = 0}^\infty {{f_n}} \left\{ { \bullet \sum\limits_{k = 1}^n {\left[ {{{\left( { - {{\not \partial }_t}} \right)}^{k - 1}} \otimes \not \partial _t^{n - k}} \right]\left( {\delta x\left( t \right) \otimes \delta y\left( t \right)} \right)} } \right\}\end{array}$

Since all zeros of 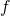$f$ are non-degenerate, we get:

$\omega = \sum\limits_a {\dot f} \left( {i{k_a}} \right)\delta {x_a}\delta {y_a}$

Now, there are nonlocal particle actions satisfying conformal symmetry as a realized symmetry of string-theory worldline reparametrization

$x\left( t \right) \to x'\left( t \right) = x\left( {t + \delta t} \right)$

In the harmonic basis:

$\left\{ {\begin{array}{*{20}{c}}{\delta t = \varepsilon {e^{{\mathop{\rm i}\nolimits} n\,t}} + c.c.}\\{\forall n \in \mathbb{Z}}\end{array}} \right.$

$c.c.$ being complex conjugation and $\varepsilon$ the infinitesimal transformation of $x$ generated by the differential operator:

${V_n} = {e^{ - i\,n\,t}}{\not \partial _t}$

and this is the crucial point: it satisfies the Virasoro algebra

$\left[ {{V_m},{V_n}} \right] = \left( {m - n} \right){V_{m + n}}$

Now, compactifying $t$ on a circle, I can normalize $t$ so that $t \in \left[ {0,2\pi } \right)$ , thus ${\left\{ {{e^{i\,n\,t}}} \right\}_{n \in \mathbb{Z}}}$ constitutes a complete basis for functions of $t$ and the Virasoro algebra is equivalent to the full reparametrization symmetry of $t$ .

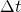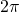Hence, a length scale is injected corresponding to the shift $\Delta t$ in $t$ that normalizes to $2\pi$ , with the Virasoro algebra generators constraining the normalization, the non-locality of particles has the gauge symmetry of the conformal group intrinsic to string theory

Solving, we get the equations of motion:

$\left\{ {\begin{array}{*{20}{c}}{x\left( t \right)\sum\limits_{k \in \not {\rm Z}} {{x_k}{e^{ - ikt}}} }\\{y\left( t \right)\sum\limits_{k \in \not {\rm Z}} {{y_k}{e^{ - ikt}}} }\end{array}} \right.$

If $f$ is symmetric, we have

$f\left( { - {{\not \partial }_t}} \right) = f\left( {{{\not \partial }_t}} \right)$

and ${z_i}$ always comes in pairs $\left( {{z_i} - {z_i}} \right)$ except for ${z_i} = 0$ or $\frac{1}{2}$ . Hence, the symplectic two-form:

$\omega = \frac{1}{2}\ddot f\left( {i{k_a}} \right)\left( {\delta {x_a}\delta {q_a} + \delta {y_a}\delta {p_a}} \right) + ...$

becomes:

$\omega = \sum\limits_{k \in \not {\rm Z}'} {i\left( {k + n} \right)} \dot f\left( {ik} \right){x_k}{y_{\left( {k + n} \right)}}$

with the conserved charges $\theta$ with $\delta x$ , $\delta y$ given by the symmetry transformation:

${Q_n} = \sum\limits_{k \in \not {\rm Z}'} {i\left( {k' + n} \right)} \dot f\left( {ik'} \right){x_k}{y_{\left( {k' + n} \right)}}$

with the creation/annihilation operators:

$\left\{ {\begin{array}{*{20}{c}}{{a_{ - k}} = {{\left( {\dot f\left( {ik} \right)k} \right)}^{1/2}}{x_k}}\\{{b_k} = {{\left( {\dot f\left( {ik} \right)k} \right)}^{1/2}}{y_k}}\end{array}} \right.$

Therefore, the symplectic two-form is equivalent to

$\omega = \sum\limits_{k \in \not {\rm Z}'} {\frac{{\delta {a_{ - k}}\delta {b_k}}}{k}}$

Important: the Virasoro algebraic constraints eliminate ghosts since the conserved charges are:

${Q_n} = \sum\limits_{k \in \not {\rm Z}'} {B\left( {n,k} \right)} \,{a_{ - k}}{b_{k + n}}$

with:

$B\left( {n,k} \right) = {\left( {\frac{{\dot f\left( {ik} \right)}}{{\dot f\left( {i\left( {k + n} \right)} \right)}}\frac{{k + n}}{k}} \right)^{1/2}}$

with non-negative spectrum upon quantization after renormalization-ordering, and so the Virasoro algebra is satisfied at the semi-classical tree-level, as evidenced by:

$\left\{ {\begin{array}{*{20}{c}}{{Q_m} \to U{Q_m}{U^{ - 1}}}\\{U = {e^{{\Sigma _k}{\lambda _k}{a_{ - 1}}{b_k}}}}\end{array}} \right.$

with the following holding:

$B\left( {n,k} \right) \to \frac{{{e^{k{\lambda _k}}}}}{{{e^{\left( {n + k} \right){\lambda _{\left( {n + k} \right)}}}}}}B\left( {n,k} \right)$

and since:

${\lambda _k} \equiv \frac{1}{{2k}}\log \left[ {k/\dot f\left( {ik} \right)} \right]$

I can deduce:

$B\left( {n,k} \right) \to 1$

Summary so far: for the action

${S^q} = - \int {dt} x\left( t \right)f\left( {{{\not \partial }_t}} \right)y\left( t \right)$

String-Theory and the String/Non-Local-‘Particles’ Duality

Nonlocal actions of particles derived via Feynman integral decomposition on a conformal hypersurface with conformal symmetry gives us a Virasoro algebra as guaranteed by Noether’s theorem

Let us look at what string-theory says about their canonical quantization

with $\left\{ {{k_a}} \right\}$ being the set of zeros of $f$ :

Since all zeros of $f$ are non-degenerate, we get:

Now, there are nonlocal particle actions satisfying conformal symmetry as a realized symmetry of string-theory worldline reparametrization

and this is the crucial point: it satisfies the Virasoro algebra

Hence, a length scale is injected corresponding to the shift $\Delta t$ in $t$ that normalizes to $2\pi$ , with the Virasoro algebra generators constraining the normalization, the non-locality of particles has the gauge symmetry of the conformal group intrinsic to string theory

with the creation/annihilation operators:

Therefore, the symplectic two-form is equivalent to

Summary so far: for the action

non-local particle theory with conformal symmetry is characterized by its spectrum $\not {\rm Z}'$ in string-theory

String-Theory and Calabi-Yau Fourfolding of M-Theory

SU(N)-Gauge-Theory from Non-Abelian Nambu-Goldstone Model

About Me

Social Networks

Archives

Login Below

Photo Gallery

Nonlocal actions of particles derived via Feynman integral decomposition on a conformal hypersurface with conformal symmetry gives us a Virasoro algebra as guaranteed by Noether’s theorem

Let us look at what string-theory says about their canonical quantization

with being the set of zeros of :

Since all zeros of are non-degenerate, we get:

Now, there are nonlocal particle actions satisfying conformal symmetry as a realized symmetry of string-theory worldline reparametrization

and this is the crucial point: it satisfies the Virasoro algebra

Hence, a length scale is injected corresponding to the shift in that normalizes to , with the Virasoro algebra generators constraining the normalization, the non-locality of particles has the gauge symmetry of the conformal group intrinsic to string theory

with the creation/annihilation operators:

Therefore, the symplectic two-form is equivalent to

Summary so far: for the action

non-local particle theory with conformal symmetry is characterized by its spectrum in string-theory

String-Theory and Calabi-Yau Fourfolding of M-Theory

SU(N)-Gauge-Theory from Non-Abelian Nambu-Goldstone Model

RELATED

F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory

Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds

The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory

About Me

Social Networks

Archives

Login Below

Photo Gallery

with $\left\{ {{k_a}} \right\}$ being the set of zeros of $f$ :

Since all zeros of $f$ are non-degenerate, we get:

Hence, a length scale is injected corresponding to the shift $\Delta t$ in $t$ that normalizes to $2\pi$ , with the Virasoro algebra generators constraining the normalization, the non-locality of particles has the gauge symmetry of the conformal group intrinsic to string theory

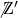non-local particle theory with conformal symmetry is characterized by its spectrum $\not {\rm Z}'$ in string-theory