Continuing from my last post where I discussed the triangular interplay between string-string duality, string field theory, and the action of Dp/M5-branes, here I shall discuss Stueckelberg string fields and derive the BRST invariance of the Landau-Stueckelberg action. Recalling that the action of M-theory in the Witten gauge is:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_M} = \frac{1}{{{k^9}}}\int\limits_{{\rm{world - volumes}}} {{d^{11}}} \sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} {T_p}^{10}d\Omega {\left( {{\phi _{INST}}} \right)^{26}}\left( {{R_{icci}} - A_\mu ^H\frac{1}{{48}}G_4^2} \right) + \\\sum\limits_{Dp} {D_\mu ^{SuSy}} {e^{ - H_3^b}}/S_{Dp}^{WV} + \sum\limits_{Dp} {D_\nu ^{SuSy}} {e^{H_3^b}}/S_{Dp}^{SV}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1a699b31134d813b59d880d2e5f88662_l3.png)
with ![]() the kappa symmetry term,
the kappa symmetry term, ![]() the metric on
the metric on ![]() , and
, and ![]() the corresponding coordinates with
the corresponding coordinates with ![]() an antisymmetric 3-tensor. Hence, the worldvolume
an antisymmetric 3-tensor. Hence, the worldvolume ![]() is:
is:
![]()
and the worldsheet action:
![]()
being the sum of three terms:
![]()
![]()
![]()
and the index I = 1, … , 22 labels 22 gauge fields: 16 coming from the internal dimensions of the heterotic string, and the other 6 gauge fields are the KK modes of the metric and antisymmetric tensor. The action ![]() has a massless spectrum given by moduli fields corresponding to deformations of the Narain lattice and thus take values in the group manifold:
has a massless spectrum given by moduli fields corresponding to deformations of the Narain lattice and thus take values in the group manifold:
![]()
Something deep has occurred: all the gauge fields of the action 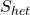 have appeared within a two-dimensional theory, and not a three-dimensional theory
have appeared within a two-dimensional theory, and not a three-dimensional theory
which is precisely the long wavelength limit behavior of the open membrane:
the gauge fields are defined in terms of fields that live on 10-dimensional boundaries of M-theory
In the closed membrane case:
the gauge fields are defined in terms of 11-dimensional fields
which brought us to the connection between string field theory and Dp-branes. Recall that one derives the string propagator by an evaluation of the Witten super-symmetric quantum path integral on a fiber-strip with the Polyakov string action:
![]()
with:
![]()
for ![]() and the Regge parameter clear from context. In the proper-time gauge and the normal modes of the lapse and shift function in 2-D, the Polyakov metric has the following property:
and the Regge parameter clear from context. In the proper-time gauge and the normal modes of the lapse and shift function in 2-D, the Polyakov metric has the following property:
![]()
allowing us to derive the open string field Polyakov propagator on the Dp-branes:
![Rendered by QuickLaTeX.com \[\begin{array}{c}G\left[ {{X_1};{X_2}} \right) = \int_0^\infty {ds} \left\langle {{X_1}\left| {\exp \left[ { - is\left( {{L_0} - i\tilde \varepsilon } \right)} \right]} \right|{X_2}} \right\rangle \\ = \left\langle {{X_1}\left| {\frac{1}{{{L_0} - i\tilde \varepsilon }}} \right|{X_2}} \right\rangle \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-89438f647f490708cfa6e25a36fb1a7c_l3.png)
with:
![]()
and the momentum operators are given by:
![Rendered by QuickLaTeX.com \[{P^\mu }\left( \sigma \right) = \frac{1}{\pi }{\left( {{p^\mu } + \sqrt 2 \sum\limits_{n = 1} {p_n^\mu \cos \left( {n\sigma } \right)} } \right)_{,\mu = 0,1,...,d}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-19aa95d541a432d36912934ee4da0545_l3.png)
![]()
Since open string end-points are topologically glued to ![]() Dp-branes, open strings must have
Dp-branes, open strings must have ![]() inequivalent quantum states and thus, the string field
inequivalent quantum states and thus, the string field ![]() has to carry the gauge group indices of
has to carry the gauge group indices of ![]() :
:
![]()
where ![]() are the generators of the SU(N) group, with
are the generators of the SU(N) group, with ![]() . Hence, the string propagator on multi-Dp-branes takes the following form, with contraction and indices ordering:
. Hence, the string propagator on multi-Dp-branes takes the following form, with contraction and indices ordering:
![]()
which yields the field theory action:
![]()
BRST-invariantly as:
![]()
Hence, the above field theory action implies that the string-string duality associates to every Dp–Brane a solution corresponding to the d–dimensional string–frame Lagrangian:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{\mathcal{L}_{S,d}} = \sqrt {\left| g \right|} \left\{ {{e^{ - 2\phi }}} \right.\left[ {R - 4{{\left( {\partial \phi } \right)}^2}} \right] + \\\frac{{{{( - )}^{p + 1}}}}{{2\left( {p + 2} \right)!}}{e^{a\phi }}\left. {F_{\left( {p + 2} \right)}^2} \right\}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e595d8bd49324003a7101ba1a1a1a8fb_l3.png)
with ![]() the dilaton,
the dilaton, ![]() the curvature of a (p + 1)–form gauge field:
the curvature of a (p + 1)–form gauge field:
![]()
where the two–index NS/NS tensor ![]() and the dual six-index heterotic five–brane tensor
and the dual six-index heterotic five–brane tensor ![]() are given by:
are given by:
![]()
and
![]()
Now we have the general form of a 10-D p-brane solution:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{ds_{S,d}^2 = {H^\alpha }dx_{\left( {p + 1} \right)}^2 - {H^\beta }dx_{\left( {D - p - 1} \right)}^2}\\{{e^{2\phi }} = {H^\gamma }}\\{{F_{0...pi}} = \delta {\partial _i}{H^{\tilde \varepsilon }}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2289bec5801dc6befb29272db1a7515b_l3.png)
with:
![]()
and:
![]()
with
![]()
The general form of 11-D Mp–branes solutions, noting the absence of the dilaton field, with the following Lagrangian:
![Rendered by QuickLaTeX.com \[{\mathcal{L}_{Ein,d}} = \sqrt {\left| g \right|} \left[ {R + \frac{1}{2}{{\left( {\partial \phi } \right)}^2} + \frac{{{{( - )}^{p + 1}}}}{{2\left( {p + 2} \right)!}}{e^{\alpha \phi }}F_{\left( {p + 2} \right)}^2} \right]\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-66fe4e93349a0e2c7ade0c36f5b8fb86_l3.png)
is:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{c}}{\alpha = - \frac{4}{N}\left( {d - p - 3} \right),}&{\beta = \frac{4}{N}\left( {p + 1} \right)}\\{\gamma = \frac{{4a}}{N}\left( {d - 2} \right),}&\begin{array}{l}{\delta ^2} = \frac{4}{N}\left( {d - 2} \right)\\\tilde \varepsilon = - 1\end{array}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5a39bda56f1832e2848d86fd66141721_l3.png)
Hence, the M2-brane solution is:
![]()
![]()
squaring the field strength gives the following M5-brane solution:
![]()
![]()
In the string-frame Ramond-Ramond gauge field Lagrangian:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{\mathcal{L}_{S,d}} = \sqrt {\left| g \right|} \left\{ {{e^{ - 2\phi }}} \right.\left[ {R - 4{{\left( {\partial \phi } \right)}^2}} \right] + \\\frac{{{{( - )}^{p + 1}}}}{{2\left( {p + 2} \right)!}}{e^{a\phi }}\left. {F_{\left( {p + 2} \right)}^2} \right\}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e595d8bd49324003a7101ba1a1a1a8fb_l3.png)
Dp-brane solutions have the following form:
![]()
![]()
![]()
From the string-string duality above and ![]() , we can derive the kinetic term of Dp–branes in terms of the Born–Infeld action with the following form:
, we can derive the kinetic term of Dp–branes in terms of the Born–Infeld action with the following form:
![]()
with the embedding metric and the gauge field world-volume curvature manifest, entailing the existence of a WZ/RR term that couples to Dp-branes:
![]()
![]()
and where the heterotic 5–brane, the IIA five–brane and the D5–brane dual potentials are given by:
![]()
![]()
![]()
Parallels for the M5-brane are formally similar. We have the quadratic kinetic term:
![]()
with the WZ term:
![]()
and the dual 6–form potential:
![]()
By the field-property of the Polyakov propagator on the Dp-branes:
![Rendered by QuickLaTeX.com \[\begin{array}{c}G\left[ {{X_1};{X_2}} \right) = \int_0^\infty {ds} \left\langle {{X_1}\left| {\exp \left[ { - is\left( {{L_0} - i\tilde \varepsilon } \right)} \right]} \right|{X_2}} \right\rangle \\ = \left\langle {{X_1}\left| {\frac{1}{{{L_0} - i\tilde \varepsilon }}} \right|{X_2}} \right\rangle \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-89438f647f490708cfa6e25a36fb1a7c_l3.png)
combined with the string-string duality, we can prove that all Dp-and-Mn–brane solutions preserve half of the SUSY. With the SUSY rules for the gravitino and dilatino in the string-frame given by:
![]()
![]()
![]()
Let us consider the gauge covariantization of the proper-time gauge and the Ramond-Ramond gauge discussed above. The action for the covariant bosonic open string field theory is implicitly defined by the BRST operator ![]() :
:
![]()
with respect to the BPZ conjugation-derived inner product, where the string field has the following Fock space expansion:
![]()
where the following holds:
![Rendered by QuickLaTeX.com \[{\phi ^{\left( 0 \right)}} = \int {\frac{{{d^{26}}p}}{{{{\left( {2\pi } \right)}^{26}}}}} \left[ {\sum\limits_{\left| f \right\rangle } {\left| {{f^{\left( 0 \right)}}} \right\rangle } {\mkern 1mu} {\psi _{\left| f \right\rangle }}\left( p \right)} \right]\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-cbe85be5d2fb3cc9cdb12969fe500ca4_l3.png)
![Rendered by QuickLaTeX.com \[{\omega ^{\left( { - 1} \right)}} = \int {\frac{{{d^{26}}p}}{{{{\left( {2\pi } \right)}^{26}}}}} \left[ {\sum\limits_{\left| g \right\rangle } {\left| {{g^{\left( { - 1} \right)}}} \right\rangle } \,{\psi _{\left| g \right\rangle }}\left( p \right)} \right]\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5599feba894a0a063dcb60518287ea32_l3.png)
for the bosonic case, and:
![]()
are the associated space-time fields. We can now write the action as:
![]()
and is invariant under the gauge transformation:
![]()
with the gauge parameter being a Grassmann string field of
![]()
given as:
![]()
In terms of ![]() and
and ![]() , the gauge transformation is expressible as:
, the gauge transformation is expressible as:
![]()
![]()
It follows then that:
![]()
is gauge invariant. Hence, in terms of ![]() , the action:
, the action:
![]()
becomes:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{S^c} = - \frac{1}{2}\left( {\left\langle {{\phi ^{\left( 0 \right)}},{c_0}{L_0}{\phi ^{\left( 0 \right)}}} \right\rangle - \left\langle {\tilde Q{\phi ^{\left( 0 \right)}},{c_0}{W_1}\left( {\tilde Q{\phi ^{\left( 0 \right)}}} \right)} \right\rangle } \right.\\ + \left. {\left\langle {{\zeta ^{\left( 1 \right)}},{c_0}{W_1}{\zeta ^{\left( 1 \right)}}} \right\rangle } \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-459699a274d6c23adea1710a8f600648_l3.png)
Note that the gauge invariance of each of:
![]()
and
![]()
entails that the string field, by conformal gauge theory, has the following form:
![]()
![]()
and we also have:
![]()
Thus, our action becomes a sum of two gauge invariant terms:
![]()
and
![]()
Now, crucially:
![]()
is equivalent to a gauge invariant action of massless vector field ![]()
and by the metaplecticity of:
![]()
it follows that gauge transformation up to level N = 1 is expandible in terms of a gauge parameter ![]() as:
as:
![]()
![]()
We perform now a Virasoro reparametrization of the evolving string surface as a transformation:
![]()
with ![]()
the wave-function of the string, which in string field theory, must be interpreted as a functional ![]() , giving us the functional action:
, giving us the functional action:
![]()
where the inner product is defined in terms of integrals over the whole string configuration space and ![]() the string field kinetic energy operator. By reparametrization invariance, we can derive the following:
the string field kinetic energy operator. By reparametrization invariance, we can derive the following:
![]()
and the following relations can be easily checked:
![]()
![]()
Now, what makes ![]() unique contrastively to
unique contrastively to ![]() is its invariance under an large group of extra symmetries in addition to reparametrization implicitly expressed by:
is its invariance under an large group of extra symmetries in addition to reparametrization implicitly expressed by:
![]()
specifically, given by shifts:
![]()
and is a type of meta-gauge symmetry acting directly on the metaplectic phase space. Let us study some properties of this metaplectic gauge group as well as ![]() .
.
We expand ![]() in terms of the eigenstates of the mass operator:
in terms of the eigenstates of the mass operator:
![Rendered by QuickLaTeX.com \[2\left( {{L_0} - 1} \right) = {p^2} + 2\left\{ {\sum\limits_{n > 0} {{\alpha _{ - n}}} \cdot {\alpha _n} - 1} \right\} = {p^2} + {M^2}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-97a4777310c0bc325097a34ff09231c5_l3.png)
where the state ![]() is annihilated by all
is annihilated by all ![]() . Then the string field functional can be written as:
. Then the string field functional can be written as:
![]()
The kinetic gauge of ![]() is given by the action of
is given by the action of ![]() on new string functionals. At first order we get the following equation of motion:
on new string functionals. At first order we get the following equation of motion:
![]()
and since ![]() satisfies:
satisfies:
![]()
it follows that:
![]()
has the property of linearized Yang-Mills gauge invariance and the following transformation laws can be derived:
![]()
![]()
where ![]() is the Chan-Paton field term.
is the Chan-Paton field term.
With ![]() a 0-level state and an eigenstate of
a 0-level state and an eigenstate of ![]() with eigenvalue
with eigenvalue ![]() , we have the following definition for the contravariant form
, we have the following definition for the contravariant form ![]()
![]()
Now we must define:
![]()
satisfying:
![]()
![]()
with the 0-th projection operator:
![]()
Combining, we have at n-th-mass level a Klein-Gordon equation:
![]()
which is gauge-invariant, thus the existence of ![]() .
.
Adding the Stueckelberg string fields to the fundamental string field ![]() , we have the local Stueckelberg action:
, we have the local Stueckelberg action:
![Rendered by QuickLaTeX.com \[S = - \frac{1}{2}\left( {\Phi - \sum\limits_n {{L_{ - n}}S_n^{Stk}\left| {2\left( {{L_0} - 1} \right)} \right|\Phi - \sum\limits_n {{L_{ - n}}S_n^{Stk}} } } \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1970ce874c046839d33427b707701c5f_l3.png)
We now define N-th-projection operators:
![]()
along with:
![]()
with
![]()
Now, since we have:
![]()
it follows that the Stueckelberg action:
![Rendered by QuickLaTeX.com \[S = - \frac{1}{2}\left( {\Phi - \sum\limits_n {{L_{ - n}}S_n^{Stk}\left| {2\left( {{L_0} - 1} \right)} \right|\Phi - \sum\limits_n {{L_{ - n}}S_n^{Stk}} } } \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1970ce874c046839d33427b707701c5f_l3.png)
is equivalent to the kinetic metaplectic gauge field action:
![]()
Now we introduce a new gauge:
![]()
At N=1 gauge field level, we thus have:
![]()
which is a hybrid Landau-Stueckelberg gauge. So for
![]()
this fixes the gauge invariance of the Stueckelberg action ![]() above.
above.
Note that under this condition, since the following holds:
![]()
any string field:
![]()
satisfies the Landau-Stueckelberg gauge condition given:
![]()
with:
![]()
![]()
This in turn entails that:
![]()
holds.
The action for this gauge condition is then:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{S_{LS}} = - \frac{1}{2}\sum\limits_{n = - \infty }^\infty {\left\langle {{\Phi _n},Q{\Phi _{ - n + 2}}} \right\rangle } - \frac{g}{3}\sum\limits_{l + m + n = 3} {\left\langle {{\Phi _l},{\Phi _m} * {\Phi _n}} \right\rangle } \\ + \sum\limits_{n = 2}^\infty {\left( {\left\langle {{{\left( {{\vartheta _{LS}}B} \right)}_{ - n + 3}},{\Phi _n}} \right\rangle + \left\langle {{{\left( {{\vartheta _{LS}}B} \right)}_n},{\Phi _{ - n + 3}}} \right\rangle } \right)} \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c6b2f5aa0b9099a658b9d594df719c23_l3.png)
with:
![]()
![]()
with the odd/even Grassmann string fields and the projection operator defined implicitly by:
![]()
Putting all together, it follows that the action ![]() is BRST invariant.
is BRST invariant.



