Space-Time Uncertainty and Non-Locality in String-Theory

By George Shiber Friday, February 17, 2017Friday, October 26, 2018 In Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Physics, Super String Theory, Supersymmetry, Witten Theory Non-Commutative Spacetime, Non-locality

Among the many truly remarkable properties of M-theory, that it is a unified theory of all interactions, including quantum gravity, and gives a completely well-defined analytic S-matrix satisfying all the axioms for a physically acceptable theory entailing Lorentz invariance, macro-causality and unitarity is perhaps the deepest, and to boot, the only quantum gravity paradigm that has that essential feature. Here, I will discuss some key aspects of nonlocality and space-time uncertainty in string theory. Let us start with an action smoothly interpolating between the area preserving Schild action and the fully reparametrization invariant Nambu–Goto action:

$I\left[ {\Phi ,X} \right] \equiv \frac{{{\mu _0}}}{2}\int\limits_\Sigma {{d^2}} \sigma \left[ {\frac{{\det \left( {{\gamma _{mn}}} \right)}}{{\Phi \left( \sigma \right)}} + \Phi \left( \sigma \right)} \right]$

where $\Phi \left( \sigma \right)$ is an auxiliary world-sheet field, ${\gamma _{mn}} \equiv {\eta _{\mu \nu }}{\partial _m}{X^\mu }{\partial _n}{X^\nu }$ the induced metric on the string Euclidean world-sheet ${x^\mu } = {X^\mu }\left( \sigma \right)$ , and ${\mu _0} \equiv 1/2\pi \alpha '$ is the string tension. Combining, we get the Nambu-Goto-Schild action:

${S_{ngs}} = - \int\limits_\Sigma {{d^2}} \xi \left\{ {\frac{1}{e}\left[ { - \frac{1}{{2{{\left( {4\pi \alpha '} \right)}^2}}}{{\left( {{\varepsilon ^{ab}}{\partial _a}{X^\mu }{\partial _b}{X^\nu }} \right)}^2}} \right] + e} \right\}$

And to make the Nambu-Goto-Schild action quadratic in space-time coordinates, we use the Virasoro constraint and an auxiliary field that transforms as a world-sheet scalar and as an anti-symmetric tensor with respect to the space-time indices:

$\left\{ {\begin{array}{*{20}{c}}{{b_{\mu \nu }}\left( \xi \right)}\\{{P^2} + \frac{1}{{4\pi \alpha '}}{{\hat X}^2} = 0,\;P \cdot \hat X = 0}\end{array}} \right.$

to yield:

Before proceeding, let us get some clarity.

Recalling the relations:

$\left\{ {\begin{array}{*{20}{c}}{\left[ {{\sigma ^m}} \right] = {\rm{length}}}\\{\left[ {{X^\mu }} \right] = {\rm{length}}}\\{\left[ \Phi \right] = 1}\end{array}} \right.$

and the world-manifold Poisson Bracket:

$\left\{ {\begin{array}{*{20}{c}}{\det \left( {{\gamma _{mn}}} \right) = {{\left\{ {{X^\mu },{X^\nu }} \right\}}^2}}\\{{{\left\{ {{X^\mu },{X^\nu }} \right\}}_{{\rm{PB}}}} \equiv {\varepsilon ^{mn}}{\partial _m}{X^\mu }{\partial _n}{X^\nu }}\end{array}} \right.$

Hence, the action:

is reparametrization invariant only if the auxiliary field $\Phi \left( \sigma \right)$ transforms as a world-sheet scalar density:

$\Phi \left( {\sigma '} \right) = \left| {\frac{{\partial \sigma }}{{\partial \sigma '}}} \right|\Phi \left( \sigma \right)$

By implementing reparametrization invariance, $\Phi \left( \sigma \right)$ can be transformed to unity and the Schild action can be recovered as a gauge-fixed form:

$I\left[ {\Phi = 1,X} \right] = \frac{{{\mu _0}}}{2}\int\limits_\Sigma {{d^2}} \sigma '\left[ {\det \left( {{\gamma _{mn}}} \right) + 1} \right] = {\rm{Schild }} + {\rm{ const}}$

Thus, by solving $\Phi \left( \sigma \right)$ in terms of $X$ from:

one recovers, on-shell, the Nambu–Goto action:

$\begin{array}{c}\frac{{\delta I}}{{\delta \,\Phi }} = 0 \to \phi = \sqrt {\det \left( {{\gamma _{mn}}} \right)} \to \\I = {\mu _0}\int\limits_\Sigma {{d^2}} \sigma \sqrt { - \det \left( {{\gamma _{mn}}} \right)} \end{array}$

The inverse equivalence relation can be deduced by starting from the Schild action:

${I_S} \equiv {\mu _0}\int\limits_\Xi {{d^2}} \varphi \det \left[ {{\gamma _{ab}}\left( \varphi \right)} \right]$

and we lift the world–sheet coordinates ${\varphi ^m}$ to the role of dynamical variables via the reparametrization ${\varphi ^m} \to {\sigma ^m} = {\sigma ^n}\left( \varphi \right)$ :

${I_{rep}} \equiv {\mu _0}\int\limits_\Sigma {{d^2}} \sigma {\Phi ^{ - 1}}\det \left[ {{\gamma _{ab}}\left( \sigma \right)} \right]$

${\Phi ^{ - 1}} \equiv {\varepsilon _{ij}}{\varepsilon ^{mn}}{\partial _m}\,{\phi ^i}{\partial _n}\,{\phi ^j}$

By a ${I_{rep}}/{\varphi ^i}$ -variation, we get the field equation:

${\varepsilon _{ij}}{\varepsilon ^{mn}}{\partial _n}{\phi ^j}\,{\partial _m}\left( {\frac{{\det \left[ {{\gamma _{ab}}\left( \sigma \right)} \right]}}{{{\Phi ^2}}}} \right) = 0$

Hence:

$\frac{{\det \left[ {{\gamma _{ab}}\left( \sigma \right)} \right]}}{{{\Phi ^2}}} = {\rm{const}} \equiv \frac{1}{{4{\mu _0}}}$

which allows us to regain the Nambu–Goto action.

Space-Time Uncertainty

Note that the fully reparametrization invariant Nambu–Goto action:

is a special case of the general two-parameter family of p-brane actions:

$I_n^p \equiv \frac{{\mu _0^{\left( {p + 1} \right)/2}}}{n}\int\limits_\Sigma {{d^{p + 1}}} \sigma e\left( \sigma \right)\left[ {\frac{{{{\left( {\det {\gamma _{mn}}} \right)}^{n/2}}}}{{e{{\left( \sigma \right)}^n}}} + n - 1} \right]$

Thus, the key notion is the geometric structure of the p-brane world volume and string world-sheet topological embedding. The whole notion then, given Witten’s results on supersymmetric quantum mechanics, for space-time uncertainty relation comes from a simple analogy concerning the nature of string quantum mechanics. The central necessary condition of string perturbation theory is world-sheet conformal invariance, and one of the key insights of string theory as a unified theory is due to conformal invariance. The elimination of the ultraviolet divergences in the presence of gravity is essentially due to modular invariance, and that is part of conformal symmetry. From the viewpoint of generic two-dimensional field theory, conformal invariance forces us to choose a very narrow class of all possible two-dimensional field theories corresponding to the fixed points of the Wilsonian renormalization group. In the final formulation of quantum mechanics, the quantization condition is replaced by the more universal framework of Hilbert spaces and the corresponding operator algebras representations. This analogy suggests the importance of reinterpreting the conformal invariance requirement by promoting it to a universal form that ultimately can be formulated in a way that does not depend on perturbative methods.

Modular invariance can be expressed as the string-reciprocity-relation of the extremal length which is a conformally invariant notion of length corresponding to families of curves on Riemann surfaces. If we take some finite region $\Omega$ and a set $\Gamma$ of arcs on $\Omega$ , the extremal length of $\Gamma$ is defined by:

$\left\{ {\begin{array}{*{20}{c}}{{\lambda _\Omega }\left( \Gamma \right) = {{\min }_s}^\rho \frac{{L{{\left( {\Gamma ,\rho } \right)}^2}}}{{A\left( {\Omega ,\rho } \right)}}}\\{L\left( {\Gamma ,\rho } \right) = {{\inf }_{\gamma \in \Gamma }}L\left( {\gamma ,\rho } \right)}\\{A\left( {\Omega ,\rho } \right) = \int_\Omega {{\rho ^2}dzd\bar z\,} }\\{{\ell _\Omega }^\Gamma \left( {L\left( {\gamma ,\rho } \right)} \right) \equiv \int_\gamma {\rho \left| {dz} \right|} }\end{array}} \right.$

in the conformal gauge. Since any Riemann surface can be composed of a set of quadrilaterals pasted along the boundaries, it is sufficient to consider the extremal length for an arbitrary quadrilateral segment $\Omega$ . Let the two pairs of opposite sides of $\Omega$ be $\left( {\alpha ,\alpha ';\beta ,\beta '} \right)$ . Take $\Gamma$ to be the set of all connected sets of arcs joining ${\alpha ,\alpha '}$ . The set of arcs joining ${\beta ,\beta '}$ is the conjugate set of arcs, denoted by ${\Gamma ^ * }$ . Hence we have two extremal lengths, ${\lambda _\Omega }\left( \Gamma \right)$ and ${\lambda _\Omega }\left( {{\Gamma ^ * }} \right)$ : then the reciprocity relation is given by:

${\lambda _\Omega }\left( \Gamma \right){\lambda _\Omega }\left( {{\Gamma ^ * }} \right) = 1$

To appreciate how the reciprocity of the extremal length reflects target space-time, consider the Polyakov amplitude for the mapping from the rectangle on a Riemann surface to a rectangular region in space-time with the side lengths $\left( {A,B} \right)$ with the boundary condition:

$\left\{ {\begin{array}{*{20}{c}}{\left( {0 \le {\xi _1} \le a,0 \le {\xi _2} \le 1} \right)}\\\begin{array}{l}{x^\mu }\left( {0,{\xi _2}} \right) = {x^\mu }\left( {a,{\xi _2}} \right) = {\delta ^{\mu 2}}B{\xi _2}/b\\{x^\mu }\left( {{\xi _1},0} \right) = {x^\mu }\left( {{\xi _1},b} \right) = {\delta ^{\mu 2}}A{\xi _1}/a\end{array}\end{array}} \right.$

Then the amplitude contains the factor:

$\exp \left[ { - \frac{1}{{\ell _s^2}}\left( {\frac{{{A^2}}}{{\lambda \left( \Gamma \right)}} + \frac{{{B^2}}}{{\lambda \left( {{\Gamma ^ * }} \right)}}} \right)} \right]$

multiplied by a power pre-factor. Hence, the quantum fluctuations of two space-time lengths $\left( {A,B} \right)$ satisfy an uncertainty relation:

$\Delta A\Delta B \sim \ell _s^2$

Recalling that all and the only legitimate observables allowed in string theory is the on-shell S-matrix, it is natural to take the above UR as setting an absolute limit, in some averaged sense, on the measurability of space-time lengths in string theory, since conformal invariance must be valid to all orders of string perturbation theory and the random nature of boundaries generally contributes to further fuzziness on the space-time lengths. This reciprocity relation reflects one of the most fundamental duality relations in string-amplitudes between ultraviolet and infrared structures. Since in the Minkowski metric one of the lengths is always dominantly time-like, the following uncertainty relation on the space-time lengths:

$\Delta T\Delta X \ge \ell _s^2$

is a universal characterization of the short-distance space-time structure of string theory.

D-branes and Yang-Mills theories

More mathematical evidence for the validity of the above UR in string theory derives from its effectiveness for D-branes. Noting that effective Yang-Mills theories for the low-velocity D-p-branes predict that the characteristic spatial transverse to D-p-branes and temporal scales of D-p-brane scattering oppositely scale with respect to the string coupling, that is:

$\left\{ {\begin{array}{*{20}{c}}{\Delta X \sim g_s^{ - 1/\left( {3 - p} \right)}{\ell _s}}\\{\Delta T \sim g_s^{1/\left( {3 - p} \right)}{\ell _s}}\\{p \ge 0\,;\,p \ne 3}\end{array}} \right.$

And though the case p = 3 is special in that the effective Yang-Mills theory is conformally invariant, the conformal transformation property actually necessitates the above space-time string theory uncertainty relation. One can easily derive the above characteristic scales in a Yang-Mills free-way. Recall that the characteristic scales:

$\left\{ {\begin{array}{*{20}{c}}{\Delta X \sim g_s^{1/3}{\ell _s}}\\{\Delta T \sim g_s^{ - 1/3}{\ell _s}}\end{array}} \right.$

of D-particle-D-particle scattering are a direct consequence of the space-time uncertainty relation and the quantum mechanical Heisenberg relation, given the fact that the mass of the D-particle is proportional to $1/{g_s}$ . All these properties are natural from the viewpoint of open string theories where the uncertainty relation (STUR):

$\Delta T\Delta X \ge \ell _s^2$

must be valid.

A deep philosophical question is that the STUR is independent of the string coupling ${g_s}$ , it appears at first that it does not take into account gravity. So the natural question is: what is its relation to the Planck scale which is the characteristic scale of quantum gravity? In string theory, the existence of gravity is a crucial consequence of the string world-sheet conformal invariance. This is due to the possibility of deforming the background space-time by a linearized gravitational wave. However, in perturbation theory, the coupling strength of the gravitational wave is an independent parameter determined by the vacuum expectation value of the dilaton. Thus, the string coupling cannot be a fundamental constant which appears in the universal non-perturbative property of string theory. So in order to take into account the Planck length for the space-time uncertainty relation (STUR), one must put that information by hand. However, I will show that by combining the Planck scale with the space-time uncertainly relation (STUR), one can derive the M-theory scale without invoking D-branes or membranes at all.

We start by reinterpreting the meaning of the Planck length using the stringy space-time uncertainties by considering the limitation of the notion of classical space-time as the background against the possible formation of virtual black holes in the short-distance regime. To probe the space-time structure in the time direction to order $\delta T$ , the Heisenberg uncertainty relation implies that the uncertainty with respect to the energy of order $\delta E \sim 1/\delta T$ is necessarily induced. Further requiring that the structure of the background space-time is not influenced by this amount of fluctuation, then the spatial scale $\delta X$ to be probed cannot be smaller than the Schwarzschild radius associated with the energy fluctuation. Hence we have:

$\delta X \ge {\left( {{G_D}\delta E} \right)^{1/\left( {D - 3} \right)}}$

in D-spacetime dimensions, setting the black-hole uncertainty relation for the characteristic gravitational scales in the form:

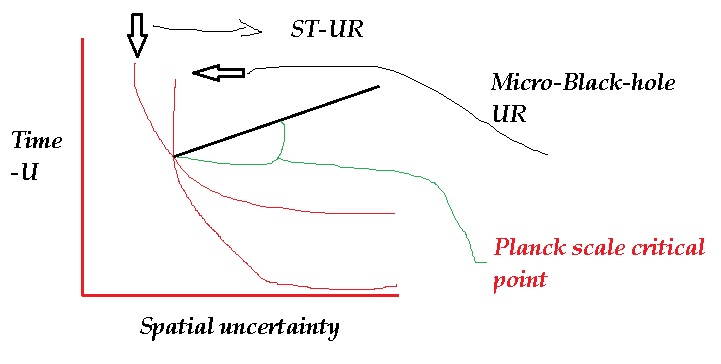
$\delta T{\left( {\delta X} \right)^7} \ge g_s^2\ell _s^8$

in D = 10 dimensional string theory, which reflects limitations only for observers at asymptotic infinity with respect to spatial and temporal resolutions below which the classical space-time structure without the formation of micro-black-holes can no longer be applied. In contrast to this, the space-time uncertainty relation sets the more fundamental limitation below which the space-time geometry itself loses its meaning. Thus, the most important characteristic scale associated with the existence of gravitation in string theory corresponds to the point of their crossover. The critical crossover scales are determined by:

$\left\{ {\begin{array}{*{20}{c}}{\Delta {X_c} \sim \delta {X_c} \sim g_s^{1/3}{\ell _s}}\\{\Delta {T_c} \sim \delta {T_c} \sim g_s^{ - 1/3}{\ell _s}}\end{array}} \right.$

And what is truly miraculous is that the spatial critical scale 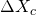$\Delta {X_c}$ coincides exactly with the M-theory scale

Space-Time Noncommutativity

The validity of the uncertainty relation (STUR):

$\Delta T\Delta X \ge \ell _s^2$

entails the existence of a noncommutative space-time structure underlying string theory. In fact, the relation:

$\exp \left[ { - \frac{1}{{\ell _s^2}}\left( {\frac{{{A^2}}}{{\lambda \left( \Gamma \right)}} + \frac{{{B^2}}}{{\lambda \left( {{\Gamma ^ * }} \right)}}} \right)} \right]$

is a string-theoretic version of the Wigner representation:

$\rho \left( {p,q} \right) \sim \exp \left[ { - \left( {{{\left( {p/\Delta p} \right)}^2} + {{\left( {q/\Delta q} \right)}^2}} \right)} \right]$

of the density matrix corresponding to the Gaussian wave packet in ‘particle’ quantum mechanics, implying that the space-time of string theory is quasi-morphic to the classical phase space in particle quantum mechanics!

Here’s how to exhibit the space-time noncommutativity of string quantum mechanics in a manifest way.

We start from a modified version of the Nambu-Goto-Schild action:

Note that the conformal invariance of string theory is now hidden in the standard Virasoro constraint:

${\tilde P^2} + \frac{1}{{4\pi \alpha '}}{X'^2} = 0$

and hence does not explicitly involve the string world-sheet auxiliary field and the world-sheet metric. It is crucial also to note that the Hamiltonian constraint comes from the following equation:

$\frac{1}{{4\pi \alpha '}}\sqrt { - \frac{1}{2}{{\left( {{\varepsilon ^{ab}}{{\not \partial }_a}{X^\mu }{{\not \partial }_b}{X^\nu }} \right)}^2}} = \varepsilon$

for the auxiliary field $\varepsilon$ . Moreover, causality in string theory is embodied in the time-like nature of the area-element:

${\varepsilon ^{ab}}{\not \partial _a}{X^\mu }{\not \partial _b}{X^\nu }$

Hence, to reformulate our action such that it becomes quadratic in the space-time coordinates, one introduces another auxiliary field ${\varpi _{ab}}\left( \xi \right)$ that transforms as a world-sheet scalar and simultaneously as an antisymmetric tensor with respect to the space-time indices:

$\begin{array}{l}{S_{ngs2}} = - \int_\Sigma {{d^2}} \xi \left\{ {\frac{1}{{4\pi \alpha '}}} \right.{\varepsilon ^{ab}}{{\not \partial }_a}{X^\mu }\\{{\not \partial }_b}{X^\nu }{\varpi _{\mu \nu }} + \left. {e\left( {\frac{1}{2}\varpi _{\mu \nu }^2 + 1} \right)} \right\}\end{array}$

allowing us to derive:

$\frac{1}{2}\varpi _{\mu \nu }^2 = 1$

which plays the role of Lagrange multiplier for the causality condition in string-theory: that is, the requirement of conformal invariance is thus essentially reinterpreted as the condition that the world-sheet field $\varpi$ be time-like. We then quantize this action by regarding the $\varpi$ -field as an external field, and given that the action is first-order with respect to the world-sheet time $\left( \tau \right)$ derivative, the system has second class constraints:

$\begin{array}{l}{\left\{ {{X^\mu }\left( {{\sigma _1}} \right),{{\not \partial }_\sigma }{\varpi _{\nu \alpha }}\left( {{\sigma _2}} \right){X^\alpha }\left( {{\sigma _2}} \right)} \right\}_D}\\ = 2\pi \alpha '\delta _\nu ^\mu \delta \left( {{\sigma _1} - {\sigma _2}} \right)\end{array}$

implying that the space ${X^i}\left( \xi \right)$ and the time ${X^0}\left( \xi \right)$ become manifestly noncommutative as evidenced by the fact that the center-of-mass time:

$T \equiv \left( {1/2\pi } \right)\int_0^{2\pi } {d\sigma } {X^0}$

and the spatial extension $X$ defined by:

$X \equiv \int {d\sigma } {\varpi _{0i}}\left( \sigma \right){\not \partial _\sigma }{X^i}$

satisfy:

$\left\{ {\begin{array}{*{20}{c}}{\left( {2\pi \alpha ' \to \ell _s^2} \right)}\\{{{\left\{ {T,X} \right\}}_D} = \ell _s^2}\end{array}} \right.$

That the expression:

$X \equiv \int {d\sigma } {\varpi _{0i}}\left( \sigma \right){\not \partial _\sigma }{X^i}$

is interpretable as the measure of spatial extension of strings can be demonstrated by recalling that in the semi-classical approximation the $\varpi$ -field is just proportional to the area element of the world-sheet of strings:

${\varpi ^{\mu \nu }} = - \frac{1}{{4\pi \alpha '}}{\varepsilon ^{ab}}{\not \partial _a}{X^\mu }{\not \partial _b}{X^\nu }/e$

and is derivable by taking the variation of the action with respect to the $\varpi$ -field.

We have thus reformulated string theory in such a way that the noncommutativity between spatial extension and time is manifest and naturally conforms to the general property:

$\Delta T\Delta X \ge \ell _s^2$

of space-time uncertainty relation derived on the basis of the string world-sheet conformal symmetry, and a paradigmatic Moyal-product argument in light of the fully reparametrization invariant Nambu–Goto action:

entails that space-time uncertainty and noncommutativity are a special case of Witten-deformation from classical space-time geometry to quantum and stringy geometry, implying non-locality. Finding a unique characterization of a stringy Witten-deformation of space-time geometry is however extremely mathematically challenging.

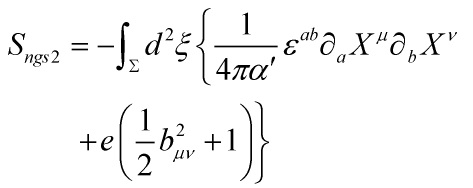
1 Response

Loop Quantum Cosmology and the Wigner-Moyal-Groenewold Phase Space
Wednesday, March 1, 2017

[…] entails that the Holst-Barbero-Immirzi 4-spinfold has the property of spacetime uncertainty that I derived for string/M-theory, an essential property if loop quantum gravity is to be a valid quantum gravity theory. As I […]