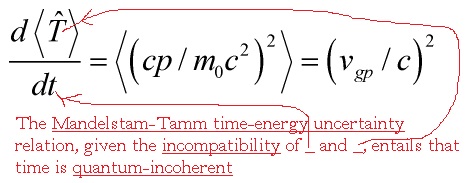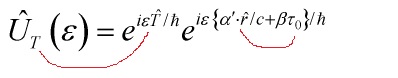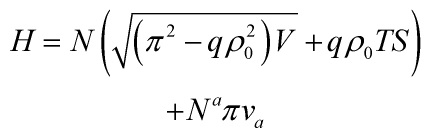As I showed, the problem of time is serious enough that it might resist any solution. From the picture above, one can see why: by a deep use of the Mandelstam-Tamm formulation of a time-energy uncertainty relation,
one can show that the problem of time may be beyond scientific resolution as such: let ![]() be the dynamical time operator in Dirac’s-RQM
be the dynamical time operator in Dirac’s-RQM
![]()
then, from:
![]()
it follows that:
![]()
hence:
and therefore:
![]()
as ![]() , and in the ultra relativistic limit
, and in the ultra relativistic limit
![]()
we have:
![]()
with
![]()
and the paradox of time is clear now: the uncertainty of the Mandelstam-Tamm time operator associated with the observable 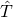 can never be matched with, nor correspond to, the time-notion in the usual uncertainty relation. Thus, one cannot generate a unitary transformation
can never be matched with, nor correspond to, the time-notion in the usual uncertainty relation. Thus, one cannot generate a unitary transformation 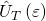 nor can time ‘
nor can time ‘ ‘ be a Schrödinger-parameter!
‘ be a Schrödinger-parameter!
note, this contradicts the diffeomorphism-invariance property of time in General Relativity and blocks the canonical Hamiltonian which generates time reparametrizations from vanishing! And, by a Dirac-Poisson argument, time cannot ‘exist’ in any quantum-gravitational cosmological setting. Let’s think outside the box while keeping this
![]()
and
in mind throughout. A solution to the PoT will always face the quantum-speed problem coupled to the Mandelstam-Tamm formulation of a time-energy uncertainty relation due to the fact that quantum-gravitational effects/regimes must dominate the Fredholm kernels of the action, and the quantum speed problem by the fundamental theorem of manifolds, entails they cannot be exterior-algebraically definable. Let me try my hand with S-Duality-(F/RF) applied to fermions dualized with reference frames where one uses Eulerian fluid dynamics of fields/’particles’ to label space-time points, and general covariance will be recovered via a re-parameterizing of the coordinate dependence. This is a deep area and touches fundamentally on quantum cosmology and quantum gravity.
Let us start with the S-Duality-(F/RF), in the real scalar field setting, with a Lagrangian function
![]()
and one performs the standard 3+1 ADM splitting of the space-time to maintain the general covariance of the theory intact, and the conjugate momentum t/p ![]()
![]()
with
![]()
combined with the 3+1 ADM splitting for 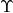 , yields the completion of the Legendre transformation, and thus the Hamiltonian will contain only spatial quantities and the conjugate momentum
, yields the completion of the Legendre transformation, and thus the Hamiltonian will contain only spatial quantities and the conjugate momentum  gives us
gives us
![]()
Incorporating the Einstein-Hilbert action, the Hamiltonian density will be the exact sum of the matter-free super-Hamiltonian and super-momentum with the scalar field terms defined as above because there are no derivatives of the metric tensor ![]() in the field action. Resulting in:
in the field action. Resulting in:
![]()
and from ADM splitting, we can derive an equivalent super-Hamiltonian in the form:
![]()
which is the Schrödinger equation for observables as the field  takes an internal time for the system. The physical Hamiltonian is hence
takes an internal time for the system. The physical Hamiltonian is hence
![]()
given i) ‘independence from ![]() ‘ condition, ii) ‘invariance under the 3-‘diff’-group’ condition, and iii) ‘invariance under re-parametrization of the time-like variable’ condition.
‘ condition, ii) ‘invariance under the 3-‘diff’-group’ condition, and iii) ‘invariance under re-parametrization of the time-like variable’ condition.
So, the equation of state in the S-Duality-(F/RF) context for the Eulerian fluid fields can be directly derived from entanglement entropy and is
![]()
with
![]()
and the 4-velocity is a combination of scalar fields and their gradients:
![]()
with ![]() the entropy per baryon. With the stress-energy tensor and the Einstein equations for matter:
the entropy per baryon. With the stress-energy tensor and the Einstein equations for matter:
![]()
One hence gets the Eulerian fluid action, after the ADM splitting:
![]()
with
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\chi _1} = {p_\alpha } = 0}\\{{\chi _2} = {p_\beta } - \alpha \pi = 0}\\{{\chi _3} = {p_\theta } = 0}\\{{\chi _4} = {p_S} - \theta \pi }\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2e1fd78c49abd93bee921e0ec4546b8f_l3.png)
and the Legendre transformation leads to the formal Hamiltonian function:
with ![]() and non-spatial quantities have been eliminated using the definition of
and non-spatial quantities have been eliminated using the definition of ![]() and the splitting of
and the splitting of ![]() .
.
Now, coupling the Eulerian fluid with general relativity, one gets the constraints-functionals:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{H = \sqrt {V\left( {{\pi ^2} - q\rho _0^2} \right)} + \sqrt q {\rho _0}ST + {H^G}}\\{{H_a} = \pi {v_a} + H_a^G}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-b3e9228150baf01f3e82880649a51222_l3.png)
Note, the algebra of these constraints is not modified by the presence of the Eulerian fluid.
Therefore, the full covariance of the model is preserved and the only secondary constraints that remain are the super-Hamiltonian and super-momentum. So they preserve their role of generators of the diffeomorphisms and exhibit a closed algebra. Solving for 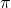 yields:
yields:
![]()
where:
![]()
and the ![]() function is now the candidate for the construction of the physical Hamiltonian: it is a scalar density of weight one,
function is now the candidate for the construction of the physical Hamiltonian: it is a scalar density of weight one, ![]() does not contain the field
does not contain the field ![]() , hence its Poisson brackets with
, hence its Poisson brackets with ![]() are vanishing, and the commutator
are vanishing, and the commutator ![]() is independent of
is independent of ![]() and vanishes!
and vanishes!
The interpretation of entropy as time variable in the co-moving frame, given S-Duality-(F/RF) boundary entropy is seen via:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\pi = - \sqrt q {\rho _0}}\\{\Xi = \sqrt q {\rho _0}ST + {H^G} = 0}\\{{\Xi _a} = H_a^G = 0}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5959b20286487fb6d5df64d89f157b1f_l3.png)
hence, the big result:
![]()
which integrated over the spatial manifold, allows us to identify the time parameter 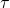 with the logarithm of the entropy per baryon, interpreting such equation as a Schrödinger-like evolution equation for observables
with the logarithm of the entropy per baryon, interpreting such equation as a Schrödinger-like evolution equation for observables
This is a temporary solution to – mind the pun – though deep, a small part of the Problem of Time, and will face problems in forthcoming posts by me.