Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

Realizing Quantum NonLocality in SuperString/M-Theory

By Posted on In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Philosophy Of Science, Physics, Super String Theory, Supersymmetry ,
photo

Here I shall discuss perhaps the deepest aspect and advantage of superstring theory, generally and as far as how rival paradigms at GUTs or quantizing gravity fare: namely, how and ‘where’ non-locality can be ‘localized’ and realized on string worldsheets and Dp-worldvolumes. Before that, I need to set the stage. Recalling that

the second quantized integral of the D-p-brane partition function for closed strings is:

    \[P_{{\rm{int}}}^{Dp} \equiv \not Z = \sum\limits_{\gamma = 0}^\infty {\underbrace {\int {{{\not D}^{SuSy}}\gamma {{\not D'}^{SuSy}}X{e^{S_{cld}^s}}} }_{{\rm{Topologies}}}} \]

where {\not D^{SuSy}} is the ‘SuSy’-superspace covariant derivative.

And, since:

    \[\begin{array}{c}\delta S_{cld}^s = - \frac{1}{{2\pi \alpha '}}\int_{\partial E_S^5} {{d^2}} \sigma d\,\Omega {\left( {{\phi _{INST}}} \right)^2}{\varepsilon ^{\alpha \beta }}{{\not \partial }_\alpha }{X^\mu }{{\not \partial }_\mu }{\lambda _\nu }\\ = - \frac{1}{{2\pi \alpha '}}\int_{\partial E_S^5} {{d^2}} d\,\Omega {\left( {{\phi _{INST}}} \right)^{ - 1/2}}\sigma \,{{\not \partial }_\mu }X\nu {\left( {{\varepsilon ^{\alpha \beta }}{{\not \partial }_\beta }{X^{^\nu }}{\lambda _\mu }} \right)^{{e^{ - H_3^b}}}}\end{array}\]

with INST the instanton, it then follows that no topology in the sum is degenerate, and thus the closed string has a solvable action in curved space-time that needs no renormalization. Matters are not that simple for the open string. The main reason being, open strings have their ends attached to D-branes of lower and odd dimensionality: max = 9, and that is key to deriving the open string partition function:

    \[P_{{\mathop{\rm int}} }^{Dp}(op) \equiv \not Z = \sum\limits_\gamma ^\infty {\underbrace {\int {{{\not D}^{SuSy}}\gamma {{\not D}^{SuSy}}X{e^{S_{open}^s}}} }_{{\rm{Brane - worldvolumes}}}} \]

where S_{open}^s is given by:

    \[S_{open}^s = {\mkern 1mu} - \frac{1}{{4\pi {\alpha ^\dagger }}}\int_{\partial E_S^5} {{d^2}} \sigma d{\mkern 1mu} \Omega {\left( {{\phi _{INST}}} \right)^2}\sigma \sqrt { - \gamma } \left( {\phi \left( {{{\bar X}^\mu }} \right)} \right.{R_{icci}} + {\gamma ^{\alpha \beta }}{\not \partial _\alpha }{X^\mu }{g_{\mu \nu }}\left( {{{\overline X }^\nu }} \right) + \frac{1}{{\sqrt { - \gamma } }}{\varepsilon ^{ - {c_{2n}}/{Y_k}\left( {{{\cos }^2}\varphi } \right)}}{\not \partial _\beta }{\overline X ^\nu }{b_{\mu \nu }}{\left( {\overline X } \right)^2}\]

with {c_{2n}} and {\Upsilon _\kappa }\left( {{{\cos }^2}\varphi } \right) the spherical harmonics on E_S^5. Now, realizing that for open strings:

    \[P_{{\mathop{\rm int}} }^{Dp}(op) \equiv \not Z = \sum\limits_\gamma ^\infty {\underbrace {\int {{{\not D}^{SuSy}}\gamma {{\not D}^{SuSy}}X{e^{S_{open}^s}}} }_{{\rm{Brane - worldvolumes}}}} \]

has a genus g suppressed by the factor:

    \[{e^{ - {\phi _{INST}}{g_{\mu \nu }}}} = {e^{ - 2{\phi _{INST}}\left( {{g_{\mu \nu }} - 1} \right)}}\quad \quad \quad {\rm{here: }}\quad \quad \quad {g_{\mu \nu }} = {e^{{{\left( {{\phi _{INST}}} \right)}^2}}}\]

it follows that one can derive, given that D-p-branes have conformal invariance, the n-loop level equation of motion with conditions

    \[\left\{ {\begin{array}{*{20}{c}}{{R_{\mu \nu }} = \, - \frac{1}{4}H_{3,\mu \lambda l}^bH_{3,\nu }^{b,\lambda \rho } + 2{{\not D}_{_\mu }}^{SuSy}{{\left( {{\phi _{INST}}} \right)}^2}{{\not D}_\nu }^{SuSy}{{\left( {{\phi _{INST}}} \right)}^{ - 1/2}}}\\{{{\not D}_\lambda }^{SuSy}{\phi _{INST}}H_{3,\lambda \mu \nu }^b - 4{{\not D}^{SuSy}}{{\left( {{\phi _{INST}}} \right)}^2}}\\{4{{\not D}^{SuSy}}{\phi _{INST}} - 4\left( {{{\not D}^{SuSy}}{{\left( {{\phi _{INST}}} \right)}^2}} \right) = {R_{icci}} + \frac{1}{{12}}{{\left( {H_3^b} \right)}^2}}\end{array}} \right.\]

with:

    \[H_{3,\mu \nu \lambda }^b = 3\,{\not \partial _{\left[ {\mu {b_\nu }\lambda } \right]}}\]

This all describes a string propagating in curved space-time that must be interpreted as a background derived from non-trivial massless open string modes, and thus pick up an infinite series of {\alpha ^\dagger } correction terms and an infinite genus correction series – so it follows that the space-time effective action is:

    \[{S_{effct}} = {\mkern 1mu} - \frac{1}{{2{\alpha ^\dagger }12}}\int {{d^{26}}} x{\mkern 1mu} d{\mkern 1mu} \Omega {\left( {{\phi _{INST}}} \right)^2}\sqrt { - \gamma } {e^{ - {\phi _{INST}}}}\left( {{R_{icci}}} \right. - 4{\left( {{\phi _{INST}}} \right)^{ - 1/2}} + \frac{1}{{12}}H_{3,\mu \nu \lambda }^bH_3^{b,\mu \nu \lambda } + ...\]

Now, since open strings can geometrically interact to form closed strings, and since closed strings give rise to the graviton and their gravitational quantum modes, and additionally, since everything gravitates, we get a highly non-trivial warping of space-time – hence, to go further in our analysis, one must consider D-p-branes in closed string theory, since a D-p-brane is a p+1 dimensional world-volume in space-time on which open strings end. The boundary conditions are:

    \[\delta {X^i} = 0\quad \quad \quad {\rm{at}}\quad \quad \quad \sigma = (0,\pi )\]

Let a D-p-brane parallel to the {x^0},{x^1},...,{x^p} dimension, and so lives at a specific location in {x^{p + 1}},...,{x^{p + 26}} dimension, we hence get the mode expansion of their fields:

    \[{X^\mu } = {x^\mu } + 2{\alpha ^\dagger }p\,\tau d\,\Omega {\left( {{\phi _{INST}}} \right)^2} + \sqrt {2{\alpha ^\dagger }i} \sum\limits_{n \ne 0} {\frac{{a_n^\mu }}{n}} \,{e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}}\cos \left( {{c_{2n}}\sigma } \right)\]

and on the transverse coordinates to the D-p-brane with boundary conditions:

    \[{X^i} = {a^i}\quad \quad \quad {\rm{at}}\quad \quad \quad \sigma = (0,\pi )\]

we get:

    \[\begin{array}{c}{\overline X ^i} = {x^i} + {w^i}\sigma + {\alpha ^\dagger }{p^i}\tau d\,\Omega \,{\left( {{\phi _{INST}}} \right)^i} + \sqrt {\frac{{{\alpha ^\dagger }}}{{2\pi i}}} \sum\limits_{n \ne 0} {\left( {\frac{{a_n^i}}{n}\,} \right.} {e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}} + \\\frac{{\overline a _n^i}}{n}{e^{ - \,{c_{2n/{\Upsilon _\kappa }}}(\cos \varphi )}}{e^{ - \,{{\left( {{\phi _{INST}}} \right)}^2}}}\left. {\left( {\tau - \sigma } \right)} \right)\end{array}\]

And so, one gets the philosophical importance of D-p-branes: they are metaplectic solitons in closed string theory, and hence, by the von Neumann boundary condition, there is a natural coupling of the super-Higgs field 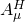A_\mu ^H to the world-sheet of a string through its boundary

    \[{S_{open}} = {S_{cld}} + \int\limits_{{\rm{end - points}}} {d\tau } A_\mu ^H{\overline X ^\mu }{e^{ - H_3^b}}d\,\Omega {\left( {{\phi _{INST}}} \right)^{\exp \,({c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}}\]

One finds then that A_\mu ^H lives on a p+1 dimensional subspace with a {\Upsilon _\kappa }(\cos \varphi ) contribution. Thus, the world-volume action is:

    \[S_{Dp}^{WV} = {S_{cld}} + \int\limits_{{\rm{end - points}}} {d\tau } A_\mu ^H{\overline X ^\mu }d\,\Omega {\left( {{\phi _{INST}}} \right)^2}{e^{ - \left( {H_3^b} \right)/{\Upsilon _\kappa }(\cos \varphi )}} + {e^{{c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}}/H_3^b\]

and by solving, one gets:

    \[\begin{array}{c}S_{Dp}^{WV} = \, - {T_p}\int {{d^{p + 1}}} x\,{e^{ - {\phi _{INST}}}}{\rm{Tr}}\left( {1 + \frac{1}{4}\left( {{F_{\mu \nu }} + d\,\Omega {{\left( {{\phi _{INST}}} \right)}^2}} \right) + {{\left( {2\pi {\alpha ^\dagger }} \right)}^{ - 1}}{b_{\mu \nu }}} \right) \cdot \\\left( {A_\mu ^H + {{\left( {2\pi {\alpha ^\dagger }} \right)}^{ - 1}}{b_{\mu \nu }}} \right) + \frac{1}{2}{{\not D}^{SuSy}}{\Upsilon _\kappa }(\cos \varphi ) - \frac{1}{4}\sum\limits_{i \times j} {\left[ {\Upsilon _{2\kappa }^i(\cos \varphi ,\Upsilon _{2\kappa }^j(\cos \varphi } \right]} \cdot \\\left[ {\Upsilon _{2\kappa }^j(\cos \varphi ),\Upsilon _{2\kappa }^i(\cos \varphi )} \right]\end{array}\]

with {T_p} \sim {\alpha ^\dagger }\frac{{p + 1}}{2} being the D-p-brane world-volume tension, and:

    \[{F_{\mu \nu }} = {\not \partial _\mu }A_\mu ^H - {\not \partial _\nu }\overline A _\mu ^H + \left[ {A_\mu ^H,\Upsilon _{2\kappa }^i(\cos \varphi } \right]\]

being the Yang-Mills field strength, and by a Paton-Chern-Simons factor, we get:

    \[\left[ {A_\mu ^H,A_\nu ^H} \right] = \sum\limits_{k = 1}^N {A_\mu ^{H,ac}} A_\nu ^{H,cb} - A_\nu ^{H,ac}A_\mu ^{H,cb}\]

and since D-p-branes warp space-time, we can deduce:

    \[\begin{array}{c}\delta {S_{open}} = \, - \frac{1}{{2\pi {\alpha ^\dagger }}}\int\limits_{{\rm{end - points}}} {{d^2}\sigma } {\varepsilon ^{\alpha \beta }}{e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}}{{\not D}_\alpha }^{SuSy}{\overline X ^\mu }{{\not D}_\beta }^{SuSy}{X^\nu }{{\not \partial }_{\mu \nu }}{\lambda _{\mu \nu }}\\ = \, - \frac{1}{{2\pi {\alpha ^\dagger }}}\int\limits_{{\rm{world - sheets}}} {{d^2}} \sigma \,{{\not \partial }_\alpha }\left( {{\varepsilon ^{\alpha \beta }}d\,\Omega {{\left( {{\phi _{INST}}} \right)}^2}} \right){{\not D}^{SuSy}}{\overline X ^\mu }{\lambda _\nu } = \\ - \frac{1}{{2\pi {\alpha ^\dagger }}}\int\limits_{{\rm{world - volumes}}} {d\tau {{\not \partial }_0}} {X^\nu }{\lambda _\nu }\,{e^{ - H_3^b/S_{cld}^s}}\end{array}\]

and finally, for the mathematical geeks ‘here’, whenever 2 or more D-branes coincide, there is a Clifford algebraic symmetry whose generators allow us to derive the total action:

    \[\begin{array}{l}{S^{Total}} = \frac{1}{{2\pi {\alpha ^\dagger }12}}\int\limits_{{\rm{world - volumes}}} {{d^{26}}} x\,d\,\Omega {\left( {{\phi _{INST}}} \right)^2}\sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} \,{e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}} \cdot \\\left( {{R_{icci}} - 4{{\left( {{{\not D}^{SuSy}}\left( {{\phi _{INST}}} \right)} \right)}^2}} \right) + \frac{1}{{12}}H_{3,\mu \nu \lambda }^bH_3^{b,\mu \nu \lambda }/A_\mu ^H + \sum\limits_{D - p - branes} {S_{Dp}^{WV}} \end{array}\]

And this is deep: because Clifford algebras are a quantization of exterior algebras, applying to ‘Einstein-Minkowski’ tangent bundle, their ‘M’-atrices, via Gaussian elimination, allow us to expand 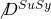{\not D^{SuSy}}, via Green-functions, and thus, by SuSy, M-Theory’s action is:

    \[{S_M} = \frac{1}{{{k^9}}}\int\limits_{{\rm{world - volumes}}} {{d^{11}}} \sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} {T_p}^{10}{\mkern 1mu} d{\mkern 1mu} \Omega {\left( {{\phi _{INST}}} \right)^{26}}\left( {{R_{icci}} - A_\mu ^H\frac{1}{{48}}G_4^2} \right) + \sum\limits_{Dp} {\not D_\mu ^{SuSy}} {e^{ - H_3^b}}/S_{Dp}^{WV} + \sum\limits_{Dp} {\not D_\nu ^{SuSy}} {e^{H_3^b}}/S_{Dp}^{SV}\]

with k the kappa symmetry gravitonic term.

The stage is set for realizing string non-locality

Some philosophical points before the mathematics: in the AdS/CFT Maldacena duality, a stack-type IIB 3-branes in the near-horizon non-Rindler geometry identifies the dynamics of string theory at the horizon consisting of open strings stuck to the Chan-Paton N=4 SUSY gauge theory of Dp-branes: by superconformal invariance, the existence of a dilatation operator on the field theory follows, and therefore there can be absolutely no locality on the AdS side, hence by duality and dimensional analysis, there can be no bulk locality. So, string theory is necessarily non-local in exactly the ‘tHooft/Susskind sense.

Back to the mathematics. Note that for continuous spacetimes, nonlocality is characterized by an infinite number of derivatives in the kinetic terms \phi f\left( {\not \partial } \right)\phi of fields. String theory is however not formulated on spacetime but its very essence makes it nonlocal: the reason being that when strings propagate, their trajectories are not, as we have seen above, one-dimensional worldlines but two-dimensional worldsheets, and so, string-interaction dynamics extends to non-pointwise finite region of space. Moreover, strings are nonlocal in the sense of their field-theory limit, since the particle-field content of the string spectrum evolves according to the nonlocal operators:

    \[f\left( {{{\not \partial }_\mu }{{\not \partial }^\mu }} \right) \sim {\not \partial _\mu }{\not \partial ^\mu }{e^{c\,\alpha '{{\not \partial }_\mu }{{\not \partial }^\mu }}}\]

\mu runs from 0 to D, c = O(1) is a constant, and \alpha ' the Regge slope, whose surface-states obey a universal diffusion-type equation whose diffusion-time is the parameter of the family, and the spatial generator is a combination of Virasoro operators. Generally and due to both, quantum and entropic entanglement reasons, nonlocal operators are deeply troublesome since the associated Cauchy problem is highly nonstandard because it gives rise to an infinite number of initial conditions \phi \left( 0 \right){\rm{, }}\dot \phi \left( o \right){\rm{, }}\ddot \phi \left( 0 \right){\rm{, }}...\,{\rm{,}} representing an infinite number of degrees of freedom, and since the Taylor expansion of \phi \left( t \right) around t = 0 is exactly given by the full set of initial conditions, specifying the Cauchy problem would be equivalent to knowing the solution itself and this makes it extremely difficult to find analytic solutions to the equations of motion. Moreover, causality will be violated at microscopic scales.

However, the type of nonlocality exhibited by

    \[f\left( {{{\not \partial }_\mu }{{\not \partial }^\mu }} \right) \sim {\not \partial _\mu }{\not \partial ^\mu }{e^{c\,\alpha '{{\not \partial }_\mu }{{\not \partial }^\mu }}}\]

present in string-field-theory, with form factors \exp H\left( {{{\not \partial }_\mu }{{\not \partial }^\mu }} \right), avoids the Cauchy and Taylor problems, and causality is respected with exponential-operators, both at the microscopic and at the macroscopic level, of the SFT form {e^{{{\not \partial }_\mu }{{\not \partial }^\mu }}}.

Thus, to show effective nonlocal action, we can, without any loss of generality, concentrate on the bosonic sector with Polyakov action for the open bosonic string being:

    \[S = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {{\rm{d}}\tau } \int_0^\pi {{\rm{d}}\sigma } \left( {{{\not \partial }_\tau }{X_\mu }{{\not \partial }_\tau }{X^\mu } - {{\not \partial }_\sigma }{X_\mu }{{\not \partial }_\sigma }{X^\mu }} \right)\]

and I gauge-fixed the worldsheet metric to the flat one by combining worldsheet diffeomorphisms and a Weyl transformation. So, from the Polyakov action, the equation of motion is:

    \[\left( { - \not \partial _\tau ^2 + \not \partial _\sigma ^2} \right){X^\mu } = 0\]

Specifying a set of boundary conditions for the free open string, these are presicely the Neumann boundary conditions

    \[{\not \partial _\sigma }{X^\mu }\left( {\tau ,0} \right) = 0 = {\not \partial _\sigma }{X^\mu }\left( {\tau ,\pi } \right)\]

Plugging the solution back into the Polyakov action, we get

    \[S = {b^{\left\langle { \pm \infty } \right\rangle }}\]

for {b^{\left\langle { \pm \infty } \right\rangle }} a constant, not necessarily finite, boundary condition term.

So, for any {X_{sol}} solution of

    \[\left( { - \not \partial _\tau ^2 + \not \partial _\sigma ^2} \right){X^\mu } = 0\]

we have:

eq1

and the last two terms vanish for the Neumann boundary conditions. However, one needs to derive an nontrivial effective action for the string in the limit where its length tends to zero and hence can be modeled as a ‘particle’. To perform such a zoom-out properly, one’s instinct is to integrate the degrees of freedom along the string length: alas, this is not possible if we specify the Neumann conditions on both endpoints of the string.  One ought then to define one of the string-endpoints via a Dirichlet boundary condition, plug the corresponding solution \bar X back into

    \[S = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {{\rm{d}}\tau } \int_0^\pi {{\rm{d}}\sigma } \left( {{{\not \partial }_\tau }{X_\mu }{{\not \partial }_\tau }{X^\mu } - {{\not \partial }_\sigma }{X_\mu }{{\not \partial }_\sigma }{X^\mu }} \right)\]

and integrate over the length parameter σ. So we get an effective action S\left[ {\bar X} \right] that hence encodes the degrees of freedom we are looking for. They correspond to a ‘particle’, but not in the usual sense of a pointwise object with local dynamics. Let’s delve deeper.

One Fourier transforms X in the worldsheet coordinate \tau:

    \[{X^\mu }\left( {\tau ,\sigma } \right) = \int_{ - \infty }^{ + \infty } {\frac{{{\rm{d}}k}}{{2\pi }}} {e^{ik\tau }}g\left( {k,\sigma } \right){x^\mu }\left( k \right)\]

with

    \[\left\{ {\begin{array}{*{20}{c}}{{x^\mu }\left( k \right): = \int_{ - \infty }^{ + \infty } {{\rm{d}}\tau '{e^{ - ik\tau '}}{x^\mu }\left( {\tau '} \right)} }\\{{x^\mu }\left( \tau \right): = {X^\mu }\left( {\tau ,0} \right)}\end{array}} \right.\]

According to

    \[{x^\mu }\left( \tau \right): = {X^\mu }\left( {\tau ,0} \right)\]

and in light of the fact that

    \[{\not \partial _\sigma }{X^\mu }\left( {\tau ,\pi } \right) = 0\]

we have:

    \[\left\{ {\begin{array}{*{20}{c}}{g\left( {k,0} \right) = 1}\\{{{\not \partial }_\sigma }g\left( {k,\sigma } \right)\left| {_{\sigma = \pi } = 0} \right.}\end{array}} \right.\]

Now, apply equation

    \[\left( { - \not \partial _\tau ^2 + \not \partial _\sigma ^2} \right){X^\mu } = 0\]

to

    \[{X^\mu }\left( {\tau ,\sigma } \right) = \int_{ - \infty }^{ + \infty } {\frac{{{\rm{d}}k}}{{2\pi }}} {e^{ik\tau }}g\left( {k,\sigma } \right){x^\mu }\left( k \right)\]

which yields the harmonic oscillator:

    \[\left( {\not \partial _\sigma ^2 + {k^2}} \right)g\left( {k,\sigma } \right) = 0\]

with solution

    \[g\left( {k,\sigma } \right) = b_k^{\left\langle { \pm \infty } \right\rangle }\sin \left( {k\sigma } \right) + {c_k}\cos \left( {k\sigma } \right)\]

Hence, the solution of

    \[\left( { - \not \partial _\tau ^2 + \not \partial _\sigma ^2} \right){X^\mu } = 0\]

 is thus

eq12

(A)

So we get the classic free-string solution:

    \[X_{{\rm{Neu}}}^\mu = {p^\mu }\tau + \sum\limits_{n \in \mathbb{Z}} {{e^{in\tau }}} \cos \left( {n\sigma } \right){x^\mu }\left( n \right)\]

which when k = n, coincides with (A). However, momenta k are continuous since the function x\left( \tau \right) is not a Cauchy-information-datum. So equation (A) represents a string where the σ = π endpoint are free and not bound to any brane. To extract a physical interpretation from (A), one must plug it into

    \[S = \frac{1}{{2\pi }}\int_{ - \infty }^{ + \infty } {{\rm{d}}\tau } \int_0^\pi {{\rm{d}}\sigma } \left( {{{\not \partial }_\tau }{X_\mu }{{\not \partial }_\tau }{X^\mu } - {{\not \partial }_\sigma }{X_\mu }{{\not \partial }_\sigma }{X^\mu }} \right)\]

and integrate over σ, and hence, that allows us to get an effective action for the endpoint coordinate {x^\mu }\left( \tau \right) which is physically interpretable as a worldline whose dynamics is characterized by a nonlocal form-factor:

eq123

(B)

with

    \[\left\{ {\begin{array}{*{20}{c}}{K\left( {{\rm{i}}k} \right) = - \frac{1}{\pi }\tan \left( {\pi k} \right)k}\\{K\left( {{{\not \partial }_\tau }} \right) = \frac{1}{\pi }\tan \left( {\pi {{\not \partial }_\tau }} \right){{\not \partial }_\tau }}\end{array}} \right.\]

and so we get

    \[S \simeq {S_{\rm{p}}} = - \frac{1}{2}\int {{\rm{d}}\tau } {x_\mu }\left( \tau \right)\not \partial _\tau ^2{x^\mu }\left( \tau \right)\]

which can always be picked by a worldline reparametrization and thus interpreted as a relativistic particle in the gauge of unit D-velocity, which implies that

    \[K\left( {{{\not \partial }_\tau }} \right)\delta {x^\mu } = 0 \Rightarrow K\left( {{{\not \partial }_\tau } + {\rm{i}}k} \right){\not \partial _\tau }{x^\mu } = 0\]

And so, by Noether’s theorem, the conserved charges associated with this symmetry are

    \[{L_n} = \frac{1}{2}\int_{ - \pi }^{ + \pi } {{\rm{d}}\tau {e^{{\rm{i}}n\tau }}} {p_\mu }\left( \tau \right){p^\mu }\left( \tau \right)\]

with:

    \[{p^\mu }: = \delta S/\delta \left( {{{\not \partial }_\tau }{x^\mu }} \right)\]

the conjugate momentum, and {L_n} obey a Virasoro algebra with vanishing central charge.

The infinite countable number of modes of the string are all contained in the operator 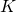K

So, define the nonlocal operator {f_0}\left( {{{\not \partial }_\tau }} \right) such that

    \[K = {\not \partial _\tau }\left( {{f_0}{{\not \partial }_\tau } \cdot } \right)\]

and so, by integrating-by-parts, the action (B) above reduces to:

    \[S = \frac{1}{2}\int {{\rm{d}}\tau } \left( {{{\not \partial }_\tau }{x_\mu }} \right){f_0}\left( {{{\not \partial }_\tau }} \right){\not \partial _\tau }{x^\mu }\]

and note that the inverse operator 1/{f_0} admits the series representation

    \[\frac{1}{{{f_0}\left( {{{\not \partial }_\tau }} \right)}} = 1 + 2\sum\limits_{n = 1}^{ + \infty } {\frac{{\not \partial _\tau ^2}}{{\not \partial _\tau ^2 + {n^2}}}} \]

Thus recasting 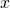x as an infinite superposition of modes

    \[{x^\mu }\left( \tau \right) = x_0^\mu \left( \tau \right) + 2\sum\limits_{n = 1}^{ + \infty } {x_n^\mu } \left( \tau \right)\]

with:

    \[\left\{ {\begin{array}{*{20}{c}}{x_0^\mu : = {f_0}\left( {{{\not \partial }_\tau }} \right){x^\mu }}\\{x_n^\mu : = \frac{{\not \partial _\tau ^2}}{{\not \partial _\tau ^2 + {n^2}}}{f_0}\left( {{{\not \partial }_\tau }} \right){x^\mu }}\end{array}} \right.\]

Hence, up to a total derivative,

    \[S = \frac{1}{2}\int {{\rm{d}}\tau } \left( {{{\not \partial }_\tau }{x_\mu }} \right){f_0}\left( {{{\not \partial }_\tau }} \right){\not \partial _\tau }{x^\mu }\]

becomes:

 

eq1234

 

And upon quantization, (B) is unitary with positive semidefinite Hamiltonian 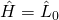\hat H = {\hat L_0}, and the generators 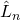{\hat L_n} obey the Virasoro algebra

    \[\begin{array}{c}\left[ {{{\hat L}_m},{{\hat L}_n}} \right] = \left( {m - n} \right){{\hat L}_{m + n}} - \\\left( {c/12} \right)m\left( {{m^2} - 1} \right){\delta _{m + n,0}}\end{array}\]

with

    \[{\hat L_n} = \left( {1/2} \right){\eta _{\mu \nu }}\sum\nolimits_{m \in \mathbb{Z}} {y_{n - m}^\mu } y_m^\nu \]

Hence, the infinite number of degrees of freedom encoded in the nonlocal action (B) are nothing but the open bosonic string spectrum. The nonlocal model realizes the same Fock space of physical states of the full theory, and the Polyakov action yields a nonlocal theory for a zoomed-out string which ‘looks’ like a particle at the zoom-limit = 0

there-is-no-royal-road-to-geometry-euclid-th-century-bc

previously

How 4-D Physics Emerges from SuperString Theory Based on Exotic 4-D Manifolds
up next

up next

SuperSymmetric Field Theory and the Quantum Master Equation
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on
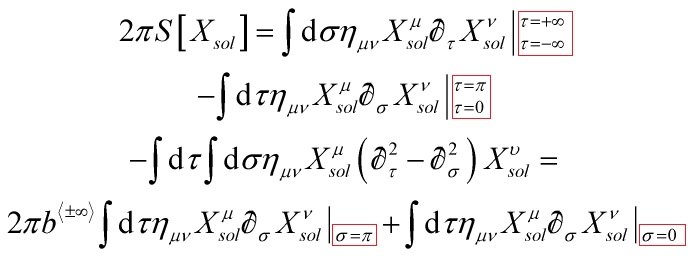
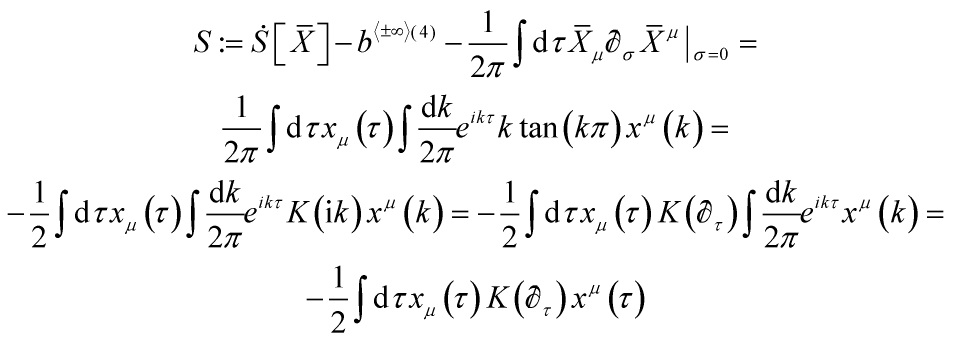
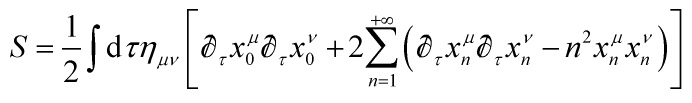
2 Responses