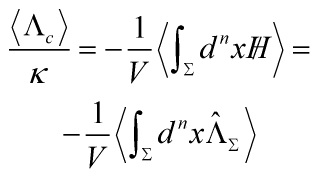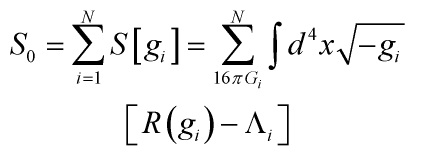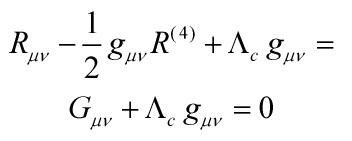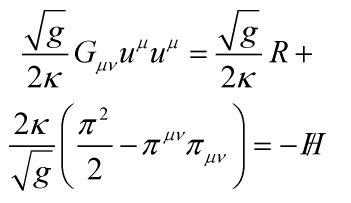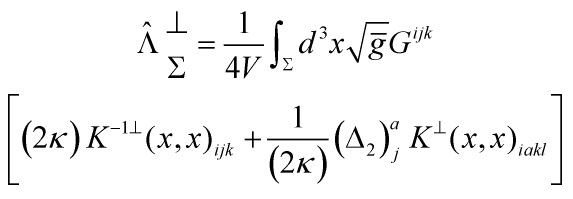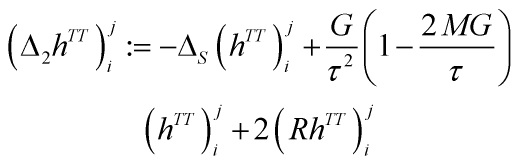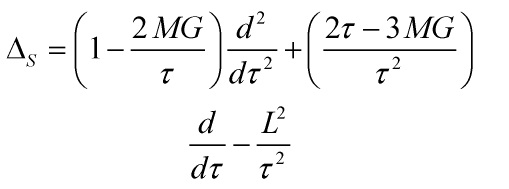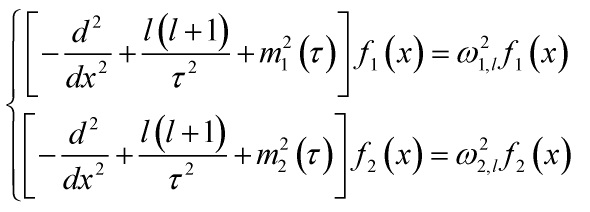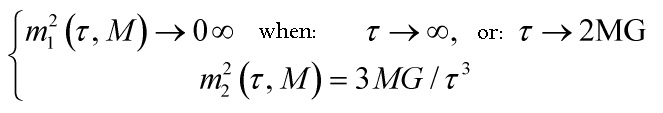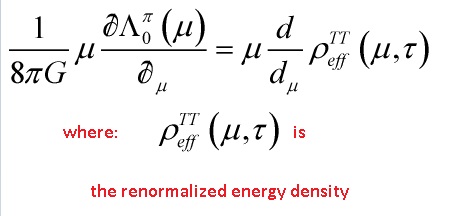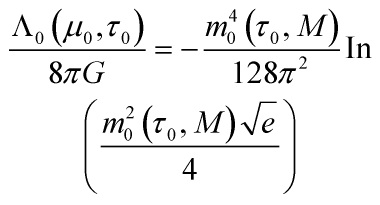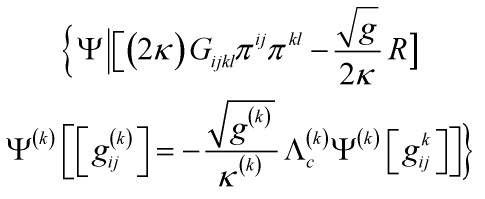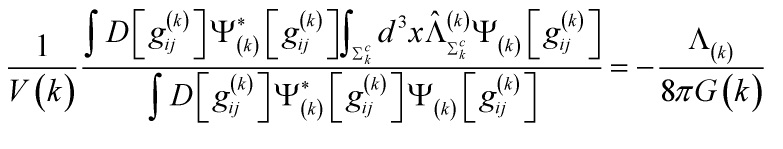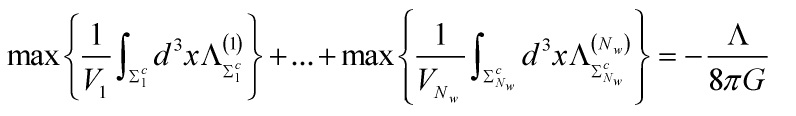Credit-address for the header photo. In this post, I will discuss and use non-linear multigravity theory to model quantum foam and probe solutions to the cosmological constant cosmic/Planck-scales ‘discrepancy paradox’, related to the hierarchy problem: namely, the 10-47GeV 4/EZP E ≈ 1071GeV cut-off one. Note first that spacetime/quantum randomness-foamy-chaos can be interpreted as a large N composition of Schwarzschild wormholes with a scalar curvature ![]() in n-dimensions being
in n-dimensions being
with ![]() the Regge-Wheeler hypersurface and let me begin with the action involving N massless gravitons without matter fields
the Regge-Wheeler hypersurface and let me begin with the action involving N massless gravitons without matter fields
with ![]() and
and ![]() being the cosmological constant and the Newton constant corresponding to the i-th universe, respectively, and the total action takes the following form
being the cosmological constant and the Newton constant corresponding to the i-th universe, respectively, and the total action takes the following form
![Rendered by QuickLaTeX.com \[{S_{tot}} = \sum\limits_{i = 1}^N {S\left[ {{g_i}} \right]} + \lambda {S_{{\mathop{\rm int}} }}\left( {{g_1},...,{g_N}} \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-68fb7ce9515f1f4e607267c93ebeae45_l3.png)
In this way, the action ![]() describes a Bose-Einstein condensates of gravitons. Start with the N = 1 Einstein field equations
describes a Bose-Einstein condensates of gravitons. Start with the N = 1 Einstein field equations
with ![]() the Einstein tensor and injecting a time-like unit vector
the Einstein tensor and injecting a time-like unit vector ![]() such that
such that ![]() yields
yields
![]()
which is the Hamiltonian constraint expressed in terms of the equation of motion. So far, we are at the classical ‘level’. The discrepancy between the observed classically-regimed cosmological constant and the quantum-numerical result is in its quantum version: that is, one can derive the expectation value
![]()
and given that
dimensional analysis for 3-D gives us
with the r.h.s. equal to
and we integrated over the Regge-Wheeler hypersurface and divided by its volume, and it can be derived starting with the Wheeler-De Witt equation which represents invariance under time reparametrization: that is the Sturm-Liouville cosmological constant problem
The boundary conditions are given by the choice of the quantum fluctuational Gaussian wavefunctionals. Extracting the TT tensor, second order in perturbation, contribution from A, of the spatial part of the metric into a background term, ![]() and a perturbation,
and a perturbation, ![]() , yields
, yields
with ![]() the inverse DeWitt metric and with the following definition
the inverse DeWitt metric and with the following definition
![Rendered by QuickLaTeX.com \[{K^ \bot }{\left( {\vec x,\vec y} \right)_{iakl}} = \sum\limits_\tau {\frac{{h_{ia}^{(\tau ) \bot }(\vec x)h_{kl}^{(\tau ) \bot }(\vec y)}}{{2\lambda (\tau )}}} \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a0f6976396787afc0a08efdfa5d895b9_l3.png)
for the propagator
![]()
with ![]() the eigenfunctions of
the eigenfunctions of ![]() .
.
Now, the expectation value of ![]() is obtained by inserting the form of the propagator into A and minimizing with respect to the variational function
is obtained by inserting the form of the propagator into A and minimizing with respect to the variational function ![]() . So, the total one loop energy density for TT tensors is
. So, the total one loop energy density for TT tensors is
![]()
and its contribution to the spin-two operator for the Schwarzschild metric is
and ![]() is the scalar curved Laplacian, given by
is the scalar curved Laplacian, given by
with
![]()
the mixed Ricci tensor
hence, the scalar curvature is traceless
Thus, we must analyse the eigenvalue equation
![]()
![]() the eigenvalue of the corresponding equation. Following Regge-Wheeler, the 3-D gravitational perturbation is represented by its even-parity form
the eigenvalue of the corresponding equation. Following Regge-Wheeler, the 3-D gravitational perturbation is represented by its even-parity form
![]()
Hence, the system
![]()
from the throat of the bridge, becomes
Hence, we have, for ![]() and
and
![]()
and
So, one can write
![]()
where we have
![]()
We can now explicitly evaluate:
![]()
in terms of the effective mass. Via the ‘t Hooft BWM method, one can derive
![Rendered by QuickLaTeX.com \[\begin{array}{c}{\rho _i}\left( \varepsilon \right) = \frac{{m_i^4\left( \tau \right)}}{{256{\pi ^2}}}\left[ {\frac{1}{\varepsilon } + {\rm{In}}\left( {\frac{{{\mu ^2}}}{{m_i^2\left( \tau \right)}}} \right) + 2\,{\rm{In}}\,2 - \frac{1}{2}} \right]\\i = 1,2\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ba99cad4870b2b3040d9a87d4c57c10c_l3.png)
by using the zeta function regularization method to numerically analyse the energy densities ![]() and by introducing the mass parameter
and by introducing the mass parameter ![]() so as to restore the correct dimension for the regularized quantities. So the energy density is renormalized due to the absorption divergences, yielding the classical constant
so as to restore the correct dimension for the regularized quantities. So the energy density is renormalized due to the absorption divergences, yielding the classical constant
removing the dependence on the mass scale ![]() , it is appropriate to use the renormalization group equation, which means imposing:
, it is appropriate to use the renormalization group equation, which means imposing:
After solving, one realizes that the renormalized constant ![]() should be treated as a running one
should be treated as a running one
and the cosmological constant takes the form
with a minimum
![]()
and the condition
![]()
We are finally in a position to discuss non-linear multigravity gas. For every gravitational field, associate the variables ![]() with the gauge
with the gauge
![]()
and introduce the domain ![]()
and a covering ![]() such that
such that
![]()
gives us
Hence, every ![]() has the topology of
has the topology of ![]() ,
,
and so the whole physical space  containing the energy density will be composed by the non overlapping spaces
containing the energy density will be composed by the non overlapping spaces 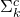 , yielding a model which is composed by
, yielding a model which is composed by 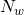 copies of the same world. Therefore, the final evaluation of the global cosmological constant can be written as
copies of the same world. Therefore, the final evaluation of the global cosmological constant can be written as
with ![]() the eigenvalue on each
the eigenvalue on each ![]() , giving us the massive graviton relation
, giving us the massive graviton relation
![]()
which together with
bridges, and thus (partially) solves, the discrepancy paradox. To be continued.