Polyakov-Zumino-Witten Analysis and ‘Einstein/String-Theory Correspondence’

By George Shiber Sunday, February 14, 2016Saturday, August 17, 2019 In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Super String Theory, Time Einstein, Friedmann-Robertson-Walker

You will find truth more quickly through delight than gravity. Let out a little more string on your kite ~ Alan Cohen

Continuing from my last post, I will establish and conclude in this post, via Polyakov/Zumino-Witten analysis, a 4-D-Einstein/String-Theory Correspondence. I last derived the $G$ -gauge invariant and generally covariant action

${S_d} = \int\limits_{{M_d}} {\left\{ {\sqrt g \phi R + {L_{mat}} + {L_{gauge}} + {L_{top}}} \right\}}$

with $\phi$ the dilaton,

$\int\limits_{{M_d}} {\left\{ {{L_{mat}} + {L_{gauge}}} \right\}}$

the matter and gauge field action, and

$\int\limits_{{M_d}} {\left\{ {{L_{top}}} \right\}}$

the topological term which picks the vacuum. Hence the partition function corresponding to

${S_d} = \int\limits_{{M_d}} {\left\{ {\sqrt g \phi R + {L_{mat}} + {L_{gauge}} + {L_{top}}} \right\}}$

is given by the polyakov-looking series

$Z\left( {{\phi _i}} \right) = \sum\limits_{M - {\rm{topologies}}}^\infty {\left\{ {\int\limits_{{M_d}} {\left[ {d{g_{\alpha \beta }}} \right]\left[ {d\Psi } \right]\left[ {dZ} \right]{e^{\frac{i}{h}{S_d}}}} } \right\}}$

Let’s delve deeper. I listed fundamentally serious problems for string-theory and to solve them, we need to describe a dynamical solution and must work in four-dimensional time-dependent geometry where the string theory is equipped with two dimensional static target space. I will show how this approach gets over the listed problems. Also, developments in string theory show that this dynamical method including quantum effects may entirely be deduced from the evolution upon the space-time invariant part ${M_2}$ with respect to ${G_{ext}}$ ; in particular, when ${M_2} = {S^2}$ . Hence, I must construct a two-dimensional equivalent action of Einstein’s equation in four dimensional ${G_{ext}}$ isometric space-time and actions describing evolution of ${G_{ext}}$ -orbits and matter on ${M_2}$ . Recalling that four-dimensional isotropic and homogeneous space-times admit six dimensional isometric group $G$ with isotropic subgroup $SO(3)$ and hence the 4-D space-time ${M_4}$ splits into three dimensional spatial part which evolves upon a one dimensional time-like ${M_1}$ according to the fibration

${f_1}:{M_4} \to {M_1}$

with group structure

$\frac{G}{{SO(3)}}$

and ${M_1}$ is the corresponding invariant part. So, the metrics are of Friedmann-Robertson-Walker type

$d{s^2} = d{t^2} + {a^2}\left( t \right)d{t^2}$

with $a\left( t \right)$ the measure-scale of the universe and $dl$ the spatial linear element. It is folklore knowledge that the Einstein equations corresponding to the Hilbert-Einstein action coupled to a scalar field, keeping this term in mind

${g^{\mu \nu }}{\not \partial _\mu }\phi \,{\not \partial _\nu }\phi - 2U\left( \phi \right)$

$S = \frac{1}{{2k}}\int\limits_{{M_4}} {{d^4}} x\left\{ {\sqrt g \left( {R + k\left[ {{g^{\mu \nu }}{{\not \partial }_\mu }\phi \,{{\not \partial }_\nu }\phi - 2U\left( \phi \right)} \right]} \right)} \right\}$

and reduce in the Friedmann-Robertson-Walker space-time to a dynamical system

$\left\{ {\begin{array}{*{20}{c}}{\frac{{dH}}{{dt}} = kU\left( \phi \right) - 3{H^2} = V\left( {\phi ,H} \right)}\\{\frac{{d\phi }}{{dt}} = \pm \sqrt { - \frac{2}{k}V\left( {\phi ,H} \right)} }\end{array}} \right.$

whose solutions supervene on whether the universe is expanding, collapsing or stationary and depend on the content of matter and initial conditions, with $H\left( t \right) = \frac{{da}}{{adt}}$ the Hubble expansion rate. This system is derivable from the action-system

$S = {S_{gra}} + {S_{mat}}$

${S_{gra}} = \int\limits_{{M_1}} {dt} \left\{ { - \frac{3}{k}a{{\left( {\frac{{da}}{{dt}}} \right)}^2}} \right\}$

${S_{mat}} = \int\limits_{{M_1}} {dt{a^3}} \left\{ {\frac{1}{2}{{\left( {\frac{{d\phi }}{{dt}}} \right)}^2} - U\left( \phi \right)} \right\}$

To complete action-system, one needs to add an action that governs the evolution of $\frac{G}{{SO(3)}}$ with respect to ${M_1}$ with the geodesic flow given by

${S_{geo}}\left( {x,g} \right) = \int\limits_{{M_1}} {dt} \sqrt h {h^{00}}{\not \partial _t}{x_i}{\not \partial _t}{x_j}{G^{ij}}$

Therefore the Friedmann-Robertson-Walker space-times dynamical evolution reduces to a quantum system

${S_{FRW}} = {S_{gra}} + {S_{mat}} + {S_{geo}}$

and the quantum fluctuation corresponding to the classical solutions are obtained from the partition function $Z$ , with this in sight

${e^{ - \left( {\frac{i}{h}{S_{FRW}}} \right)}}$

$Z = \sum\limits_{{M_1} - top} {\int\limits_{{M_1}} {\left[ {dh} \right]} } \left[ {dx} \right]\left[ {d\phi } \right]{e^{ - \left( {\frac{i}{h}{S_{FRW}}} \right)}}$

Such a reduction of the Einstein equation coupled to matter in Friedmann-Robertson-Walker universe to dynamics governing the evolution upon the cosmic time $\tau$ , extend to the spherical case. Now, a four-dimensional spherical space-time ${M_4}$ admits $SO(3)$ isometry group with its isotropic subgroup $SO(2) \equiv U(1)$ . This entails the existence of a fibration

${f_2}:{M_4} \to {M_2}$

with structure group $SO(3)/U(1)$ and the base space ${M_2}$ is the invariant part of ${M_4}$ relative to $SO(3)$ . Thus, there exist a coordinates system upon which the ${M_4}$ metric is

$d{s^2} = {h_{\alpha \beta }}d{\sigma ^\alpha }d{\sigma ^\beta } + {g_{ij}}d{x^i}d{x^j}$

$\left( {{h_{\alpha \beta }}} \right)$ is the metric with the time-like coordinate ${\sigma ^0} = \tau$ and the spatial one ${\sigma ^1} = \sigma$ . $\left( {{g_{ij}}} \right)$ being the $SO(3)/U(1)$ metric with coordinates $\left( {{x^2},{x^3}} \right)$ . In the commoving frame and spherical coordinates $\left( {r,\theta ,\varphi } \right)$ the metric is

$\begin{array}{c}d{s^2} = d{\tau ^2} + - {e^\lambda }d{r^2} - {e^{2\mu }} \cdot \\\left( {d{\theta ^2} + {{\sin }^2}\theta d{\varphi ^2}} \right)\end{array}$

The corresponding Einstein equations reduces to a dynamical system on the phase space with the action

${S_{gr}}\left( {\mu ,\lambda } \right) = \int\limits_{{M_2}} {{d^2}} \sigma \not L\left( {\mu ,\dot \mu ,\lambda ,\dot \lambda } \right)$

The natural corresponding action is $SO(3)/U(1)$ -gauge invariant and ${M_2}$ generally covariant, so the Yang-Mills term vanishes and one gets a $SO(3)/U(1)$ Wess–Zumino–Witten model

${S_{WZW}} = \int\limits_{{M_2}} {{d^2}} \sigma \sqrt h {h^{\alpha \beta }}{\not \partial _\alpha }{x^i}{\not \partial _\beta }{x^j}{g_{ij}}$

${x_i}$ , ${g_{ij}}$ are respectively the $SO(3)/U(1)$ coordinates and metric. ${\sigma ^\alpha }$ and $\left( {{h_{\alpha \beta }}} \right)$ are their ${M_2}$ analogue. Contribution of fields ${\varphi _i}$ gets from the action

${S_{mat}} = \sum\limits_i {\int\limits_{{M_2}} {{d^2}} } \sigma {A_i}\left( x \right){\phi _i}\left( x \right)$

with ${A_i}$ the composites of $SO(3)/U(1)$ coordinates and their derivatives with respect to ${M_2}$ .

Hence, the evolution of the Einstein-matter system in four-dimensional spherical space-time is obtained from the action principle

${S_2} = {S_{gr}} + {S_{WZW}} + {S_{mat}}$

and the quantum fluctuation about its classical solutions are obtained from the partition function

${Z_2} = \sum\limits_{{M_2} - top} {\int\limits_{{M_2}} {\left[ {dh} \right]} } \left[ {dx} \right]\left[ {d\phi } \right]{e^{ - \left( {\frac{i}{h}{S_2}} \right)}}$

and the deep point is that this reflects that there is uncertainties only in the geometry and topology of ${M_2}$ and position in the orbit-coordinates.

The philosophical upshot then of the this and the previous post is that at fundamental scales the universe is four dimensional and spherical. Law-governing evolution of matter and geometry upon ${M_2}$ is a formal string theory with the following correspondences:

String Framework $\Rightarrow$ world-sheet ${\Sigma _g}$
The Polyakov’s spin factor $\Rightarrow$ the action representing a static two dimensional space-time sigma-model

The present framework we deduced

The 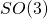$SO(3)$ invariant part of ${M_2}$ with coordinates including the time variable 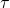$\tau$
The partition function of 2-D quantum gravity with action representing the fundamental evolution of matter in four-dimensional space-time constitutes a cosmological scenario where we can evaluate quantum effects. To carry out this scenario we need to determine the action ${S_{gra}}$ .

Let me derive the two-dimensional action ${S_{grav}}\left( {\lambda ,\mu } \right)$ equivalent to Einstein equations coupled to matter

${R_{\mu \nu }} - \frac{1}{2}R\frac{{8\pi G}}{{{C^4}}}{T_{\mu \nu }}$

in four-dimensional spherical space-times in the H-dynamic case

${T_{\mu \nu }} = \left( {\rho + \varepsilon } \right){v_\mu }{v_\nu } + p{g_{\mu \nu }}$

with $p = k\varepsilon$ and let me analyze the symmetries. Note, the non-vanishing components of the energy-momentum tensor ${T_{\mu \nu }}$ are ${{\rm T}_{00}}$ , ${{\rm T}_{11}}$ , ${{\rm T}_{22}}$ , ${{\rm T}_{33}}$ , and ${{\rm T}_{10}}$ the space-time metric writes as

$\begin{array}{c}d{s^2} = d{\tau ^2} + {e^{ - \lambda }}d{r^2} - {e^{2\mu }} \cdot \\\left( {d{\theta ^2} - {{\sin }^2}\theta d{\varphi ^2}} \right)\end{array}$

Hence, the Einstein equations are given by

$\begin{array}{c}\frac{1}{4}{e^{ - \lambda }}\left( {\frac{{\mu '}}{2} + \mu '\nu '} \right) - {e^{ - \nu }}\left( {\ddot \mu - \frac{1}{2}\dot \mu \dot \nu + \frac{3}{4}{{\dot \mu }^2}} \right)\\ - {e^{ - \mu }} = \frac{{8\pi G}}{{{C^4}}}T_1^1\end{array}$

$\begin{array}{c}\frac{1}{4}{e^{ - \nu }}\left( {2\nu '' + {{\nu '}^2} + 2u'' + {{u'}^2} - u'\lambda ' - \nu '\lambda ' + u'\nu '} \right)\\ + \frac{1}{4}{e^{ - \nu }}\left( {\nu \dot \lambda + \dot \nu \dot \mu - \dot \mu \dot \lambda - 2\ddot \lambda {{\dot \lambda }^2} - 2\ddot u - {{\dot u}^2}} \right)\\ = \frac{{8\pi G}}{{{C^4}}}T_0^0\end{array}$

$\begin{array}{c} - {e^{ - \lambda }}\left( {\ddot u + \frac{3}{4}{{u'}^2} - \frac{{u'\lambda '}}{4}} \right) + \\\frac{1}{2}{e^{ - \nu }} + \frac{1}{2}{{\dot u}^2} + {e^{ - \mu }} = \frac{{8\pi G}}{{{C^4}}}T_0^0\end{array}$

with the existence of covariant conservation equations

${\nabla ^\mu }{T_{\mu \nu }} = 0$

Hence, with

$\left\{ {\begin{array}{*{20}{c}}{\nu ' = \frac{{2p'}}{{p + \varepsilon }}}\\{\left( {2\dot \mu + \dot \lambda } \right) = - \frac{{2\dot \varepsilon }}{{p + \varepsilon }}}\end{array}} \right.$

and the constraint $p = k\varepsilon$ , we can finally derive the desired action

${S_{grav}} = \int\limits_{{M_2}} {\not L} \left( {\lambda ,\mu ,\dot \mu ,\dot \lambda ,\dot \mu ,\dot \nu } \right)d\tau dr$

with

$\not L = {\not L_1} + {\not L_2} + {\not L_3}$

where we have

$\begin{array}{c}{{\not L}_1} = \left\{ {\frac{{{{u'}^2}}}{2} + ku'\left( {\lambda ' + u'} \right)} \right\} \cdot \\\exp \left[ { - \frac{{k + 1}}{2}\lambda + \left( {k + 1} \right)u} \right]\end{array}$

$\begin{array}{c}{{\not L}_2} = \left\{ {{{\dot u}^2} + \dot \mu \dot \lambda } \right\} \cdot \\\exp \left[ { - \frac{{k - 1}}{2}\lambda + \left( {1 + k} \right)u} \right]\end{array}$

${\not L_3} = 2\exp \left[ {\frac{{k + 1}}{2}\lambda + ku} \right]$

which gives us the ‘Einstein/String-Theory Correspondence’ from a careful Riemannian analysis of

${S_{grav}} = \int\limits_{{M_2}} {\not L} \left( {\lambda ,\mu ,\dot \mu ,\dot \lambda ,\dot \mu ,\dot \nu } \right)d\tau dr$

and an alternative description of string theory with a two dimensional static target space describing dynamical quantum effects, in four dimensional symmetric and time-dependent geometry. This permits us to deal with the problem of time-dependent solutions of string theory and the inadequate interpretation of its building blocks and whose action is conformally invariant at the Planck-regime.