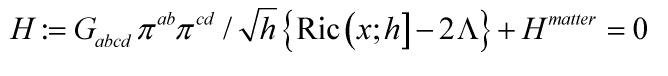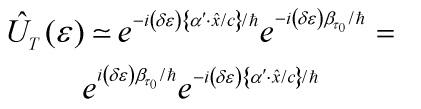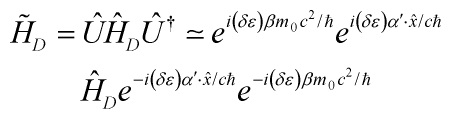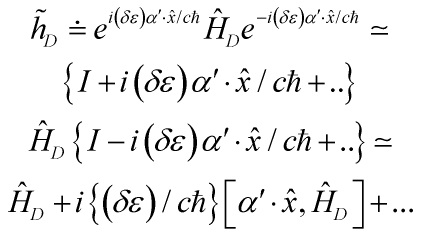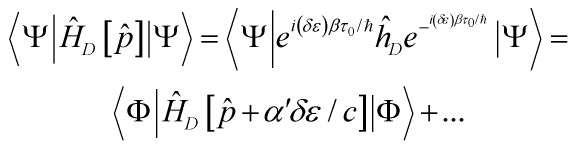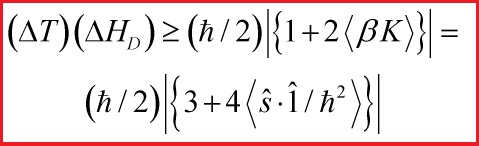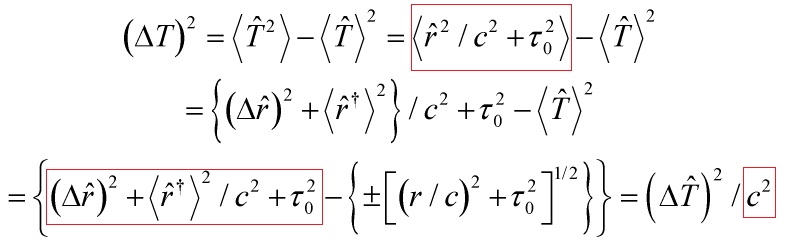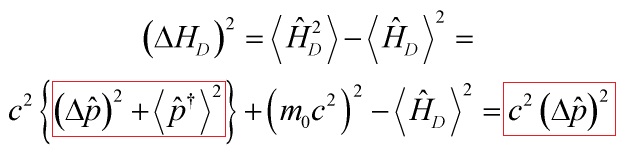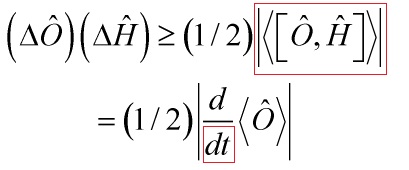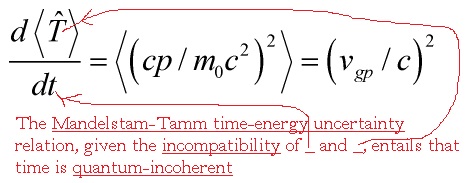On the Problem of Time in Quantum Physics

By George Shiber Monday, June 13, 2016Friday, October 26, 2018 In Cosmology, Grand Unification Physics, Mathematical Physics, Mathematics, Philosophy, Philosophy Of Physics, Philosophy Of Science, Physics, Time Dirac, Mandelstam-Tamm

The problem of ‘time’ (PoT) in physics is as varied as there are interpretations of the formalism of quantum mechanics. I shall set up the two hardest aspects of the problem and expand and delve deeper in subsequent writings. A familiar summation of the problem is in terms of the dichotomy between time as a Schrödinger-parameter as opposed to a ‘dynamical’-M-operator, as well as how that collides with time as it occurs in quantum cosmology, and before discussing the foundational problem, here is how time can be seen as paradoxical. The deepest aspect of the PoT is revealed in any canonical or backround-independent attempt at quantizing GR: and that is the problem of a constraint that is quadratic in the momenta however contains no linear dependence on the momenta. To visualize, here is the Wheeler–DeWitt equation (WdW)

and for GR, the Hamiltonian constraint is

and elevating any equation with a momentum dependence of the above kind to the quantum level cannot give a time-dependent wave equation such as

$\left\{ {\begin{array}{*{20}{c}}{i{{\not \partial }^\dagger }\Psi /\not \partial t = {{\hat H}_{WdW}}\Psi }\\{i\not \partial \Psi /\not \partial t = {{\hat H}_{WdW}}\Psi }\end{array}} \right.$

for a place-holder ‘t’ and some quantum Hamiltonian as one ought to expect, but paradoxically, a stationary-frozen-timeless equation

${\hat H_{WdW}}\Psi = 0$

and as can be seen by interpreting the above WdW-equation, time ‘disappears’! This is a paradox, unlike attempts to explain it away by distinguishing cosmic versus micro-subsystems ‘within’ the universe not subject to the WdW-WE, and the reason being that in Dirac’s relativistic quantum mechanics formalism, one can introduce a dynamical time operator

$\hat T = \alpha ' \cdot {\hat x^\dagger }/c + \beta {\tau _0}$

that is self-adjoint and does generate a unitary transformation

${\hat U_T}(\varepsilon ) = {e^{i\varepsilon \hat T/\hbar }}{e^{i\varepsilon \left\{ {\,\alpha ' \cdot \,\hat r/c + \beta {\tau _0}} \right\}/\hbar }}$

and the Dirac Hamiltonian eigenvalue equation

$\hat T\left| \tau \right\rangle = \tau \left| \tau \right\rangle$

holding and it gives

$\tau = \pm \,{\tau _\tau } = \pm {\left[ {{{\left( {\tau /c} \right)}^2} + \tau _0^2} \right]^{1/2}}$

${\hat T^2} = {\left( {\hat r'/c} \right)^2} + \tau _0^2$

with the ‘time eigenvectors’ being

$\left| { \pm \,{\tau _\tau }, \pm \frac{1}{2}} \right\rangle = u_\tau ^i\left| {\tau '} \right\rangle$

for i = 1, 2, 3, 4, … and ${\tau _{_0}}$ is an invariant quantity in the $\left( {\tau ',\tau } \right)$ space as ${m_0}{c^2}$ in the $\left( {\hat p,E} \right)$ space:

${\left( {{m_0}{c^2}} \right)^2} = {E^2} - {\left( {c\hat p} \right)^2}$

noting that $\varepsilon$ is ‘real’ and has the dimensions of the energy of the system under consideration. Here is where things get paradoxical: first note, for infinitesimal transformations $\delta \varepsilon \ll 1$ , we can write

$\begin{array}{c}\left[ {i\left( {\delta \varepsilon } \right)\left( {\alpha ' \cdot \hat x} \right)/c\hbar ,i\left( {\delta \varepsilon } \right){\beta _{{\tau _o}}}/\hbar } \right]\\ \propto {\left( {\delta \varepsilon } \right)^2} \approx 0\end{array}$

Thus, the Hamiltonian becomes

To set up the PoT, consider

Now using

${\hat U_T}(\varepsilon ) = {e^{i\varepsilon \hat T/\hbar }}{e^{i\varepsilon \left\{ {\,\alpha ' \cdot \,\hat r/c + \beta {\tau _0}} \right\}/\hbar }}$

we get

$\begin{array}{c}\left[ {\alpha ' \cdot \hat x,{{\hat H}_D}} \right] = 3ic\hbar I + 2{{\hat H}_D} \cdot \\\left\{ {\alpha ' - c\hat p/{{\hat H}_D}} \right\} \cdot \hat r\end{array}$

Hence, the unitary transformation induces a shift in momentum by the amount

$\delta \hat p = \left\{ {\left( {\delta \varepsilon } \right)/c} \right\}\alpha ' = \left\{ {\left( {\delta \varepsilon } \right)/{c^2}} \right\}c\alpha '$

with a Zitterbewegung behavior in the associated propagator

$U(t) = {e^{ - i{{\hat H}_D}t/\hbar }}$

thus obtaining a momentum displacement $\Delta \hat p$ whose expectation value is

$\left\langle {\Delta \hat p} \right\rangle = \left( {\varepsilon /{c^2}} \right){v_{gp}} = \gamma {m_0}{v_{gp}}$

where

$\gamma = {\left\{ {1 - {{\left( {{v_{gp}}/c} \right)}^2}} \right\}^{ - 1/2}}$

is the Lorentz factor and ${v_{gp}}$ the group velocity. By a shift argument, we have

with

$\left| \Phi \right\rangle = {e^{i\left( {\delta \varepsilon } \right){\beta _{{\tau _0}}}/\hbar }}\left| \Psi \right\rangle$

and the phase shift being

$\delta \varphi = \left( {\delta \varepsilon } \right){\beta _{{\tau _0}}}/\hbar$

Any expectation value of a finite transformation is given as

$\left\{ {\begin{array}{*{20}{c}}{\left\langle {\Delta \varphi } \right\rangle = \left\{ {\left( {\Delta \varepsilon } \right){\tau _0}/\hbar } \right\}}\\{\left\langle \beta \right\rangle = \pm \left( {1/\gamma } \right){m_0}{c^2}{\tau _0}/\hbar }\end{array}} \right.$

$\left\langle \beta \right\rangle = {m_0}{c^2}/\left\langle {{{\hat H}_D}} \right\rangle = \pm \,{m_0}{c^2}/\varepsilon = \pm 1/\gamma$

yielding the de Broglie wave length, that is, the product of the phase velocity by the period derived from the Planck relation $\varepsilon = hv$ , as originally postulated by de Broglie.

Thus, the dynamical time operator

$T = \alpha ' \cdot \hat r/c + \beta h/{m_0}{c^2}$

generates the Lorentz boost that induces the de Broglie wave, and crucially, the unitary operator

${U_{{H_D}}}\left( {\delta t} \right) = {e^{i\left( {\delta t} \right)\left\{ {\,\alpha ' \cdot \hat p + \beta {m_0}{c^2}} \right\}/\hbar }}$

can be approximated by

$U\left( {\delta t} \right) \simeq {e^{i\left( {\delta t} \right)\left\{ {\,\alpha ' \cdot \hat p/\hbar } \right\}}}{e^{i\left( {\delta t} \right)\left\{ {\,\beta {m_0}{c^2}/\hbar } \right\}}}$

therefore, from

given the Lorentz boost,

we can conclude that the associated quantum speed limit – which is a fundamental measure of the Planck-bound for the evolution time of quantum systems and quantifies the geometric distance between quantum states – for any dynamical system evolving in time and with respect to time, is undefinable in principle, and by Stone’s theorem, this contradicts the fact that the dynamical self-adjoint ‘time operator’ is the generator of the unitary transformation

${\hat U_T}(\varepsilon ) = {e^{i\varepsilon \hat T/\hbar }}{e^{i\varepsilon \left\{ {\,\alpha ' \cdot \,\hat r/c + \beta {\tau _0}} \right\}/\hbar }}$

It gets ‘worse’ and deeper still, since the time operator and the Dirac Hamiltonian necessarily satisfy the following commutaion relation

$\begin{array}{c}\left[ {\hat T,{{\hat H}_D}} \right] = i\hbar \left\{ {I + 2\beta K} \right\} + \\2\beta \left\{ {{\tau _0}{{\hat H}_D} - {m_0}{c^2}\hat T} \right\}\end{array}$

and $K$ a constant of motion:

$K = \beta \left( {2\hat s \cdot \hat 1/{\hbar ^2} + 1} \right)$

hence we have an Uncertainty-Relation:

Stronger yet:

as well as

thus we get

$\left( {\Delta \hat T} \right)\left( {\Delta \hat H} \right) = \left( {\Delta \hat r} \right)\left( {\Delta \hat p} \right) \ge \left( {\hbar /2} \right)$

which is Bohr’s interpretation in the sense that the width of a wave packet, complementary to its momentum dispersion, measures the uncertainty in the time of passage at a certain point, and is thereby complementary to its energy dispersion

And here is the deepest part: within standard QM, as an observable, the time operator is subject to the Mandelstam-Tamm formulation of a time-energy uncertainty relation. That is, any observable $\hat O$ represented by a self-adjoint operator not explicitly dependent on time, satisfies the dynamical equation:

$\left( {i\hbar } \right)\frac{d}{{dt}}\left\langle {\hat O} \right\rangle = \left\langle {\left[ {\hat O,\hat H} \right]} \right\rangle$

and from $\left[ {\hat O,\hat H} \right]$ it does follow that the uncertainties defined: $\Delta \hat O$ and $\Delta \hat H$ , obey the following relation

And, corresponding to any system observable $\hat O$ , an associated time uncertainty is defined as:

$\Delta \hat T_{\hat O}^{MT} = \frac{{\Delta \hat O}}{{\left| {\frac{d}{{dt}}\left\langle {\hat O} \right\rangle } \right|}}$

From

$\left( {\Delta \hat T} \right)\left( {\Delta \hat H} \right) = \left( {\Delta \hat r} \right)\left( {\Delta \hat p} \right) \ge \left( {\hbar /2} \right)$

and

$\left( {i\hbar } \right)\frac{d}{{dt}}\left\langle {\hat O} \right\rangle = \left\langle {\left[ {\hat O,\hat H} \right]} \right\rangle$

it follows that

$\left( {\Delta \hat T_{\hat O}^{MT}} \right)\left( {\Delta \hat H} \right) \ge \left( {\hbar /2} \right)$

which is exactly the Mandelstam-Tamm time-energy uncertainty relation

Note,

$\Delta \hat T_{\hat O}^{MT}$

is the quantum-time required for the center 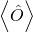$\left\langle {\hat O} \right\rangle$ of this distribution to be displaced by an amount equal to its width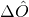 $\Delta \hat O$

Now, to show that the problem of time may be beyond scientific resolution, let $\hat O$ be the dynamical time operator in Dirac’s-RQM

$\hat O \equiv \hat T = \left( {\alpha ' \cdot \hat r} \right)/c + \beta {\tau _0}$

then, from:

$\left( {\Delta \hat T_{\hat O}^{MT}} \right)\left( {\Delta \hat H} \right) \ge \left( {\hbar /2} \right)$

it follows that:

$\frac{{\Delta \hat T}}{{\left\langle {I + 2\beta K} \right\rangle }}\left( {\Delta {{\hat H}_D}} \right)\left( {\hbar /2} \right)$

hence:

and therefore:

$\Delta T_{\hat T}^{MT} \simeq \frac{{\Delta \hat T}}{{{{\left( {{v_{gp}}/c} \right)}^2}}} \gg \Delta \hat T$

as ${v_{gp}} \ll c$ , and in the ultra relativistic limit

$\left\langle {{{\hat H}_D}} \right\rangle \simeq cp$

we have:

$\hat T\left( t \right) \simeq t + {\left( {{m_0}{c^2}/cp} \right)^2}{\tau _0} + \underbrace {...}_{{\rm{no sum}}} \simeq t$

with

$\hat T\left( t \right) \simeq {\tau _0} + {\left( {cp/{m_0}{c^2}} \right)^2}t + \underbrace {...}_{{\rm{no sum}}}$

and the paradox of time is clear now: the uncertainty of the Mandelstam-Tamm time operator associated with the observable 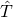$\hat T$ can never be matched with nor correspond to the time-notion in the usual uncertainty relation. Thus, one cannot generate a unitary transformation 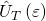${\hat U_T}\left( \varepsilon \right)$ nor can time ‘ $t$ ‘ be a Schrödinger-parameter!

We have just scratched the surface. This is an unending post that expands constantly, mind the double-puns.

On the Problem of Time in Quantum Physics

which is Bohr’s interpretation in the sense that the width of a wave packet, complementary to its momentum dispersion, measures the uncertainty in the time of passage at a certain point, and is thereby complementary to its energy dispersion

which is exactly the Mandelstam-Tamm time-energy uncertainty relation

is the quantum-time required for the center $\left\langle {\hat O} \right\rangle$ of this distribution to be displaced by an amount equal to its width $\Delta \hat O$

The AdS/CFT Duality, Time, and Spacelike Branes

S-Duality, Entropy and the Problem of Time in Quantum Physics

About Me

Social Networks

Archives

Login Below

Photo Gallery

which is Bohr’s interpretation in the sense that the width of a wave packet, complementary to its momentum dispersion, measures the uncertainty in the time of passage at a certain point, and is thereby complementary to its energy dispersion

which is exactly the Mandelstam-Tamm time-energy uncertainty relation

is the quantum-time required for the center of this distribution to be displaced by an amount equal to its width

The AdS/CFT Duality, Time, and Spacelike Branes

S-Duality, Entropy and the Problem of Time in Quantum Physics

RELATED

F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory

Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds

The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory

About Me

Social Networks

Archives

Login Below

Photo Gallery

is the quantum-time required for the center $\left\langle {\hat O} \right\rangle$ of this distribution to be displaced by an amount equal to its width $\Delta \hat O$