Eleven-dimensional supergravity on Calabi-Yau orbifolds naturally induces ![]() exceptional symmetries in
exceptional symmetries in ![]() that can be realized as U-duality symmetries of M-theory upon
that can be realized as U-duality symmetries of M-theory upon ![]() -discretization and without Betti-truncations. Hence, exceptional field theory based on the modular group
-discretization and without Betti-truncations. Hence, exceptional field theory based on the modular group ![]() uses a dimensionally extended spacetime to 12-D that fully covariantizes supergravity under the U-duality symmetry group of M-theory. Taking full advantage of the M/F-theory duality, and Kovalev’s twisted connected sum constructed
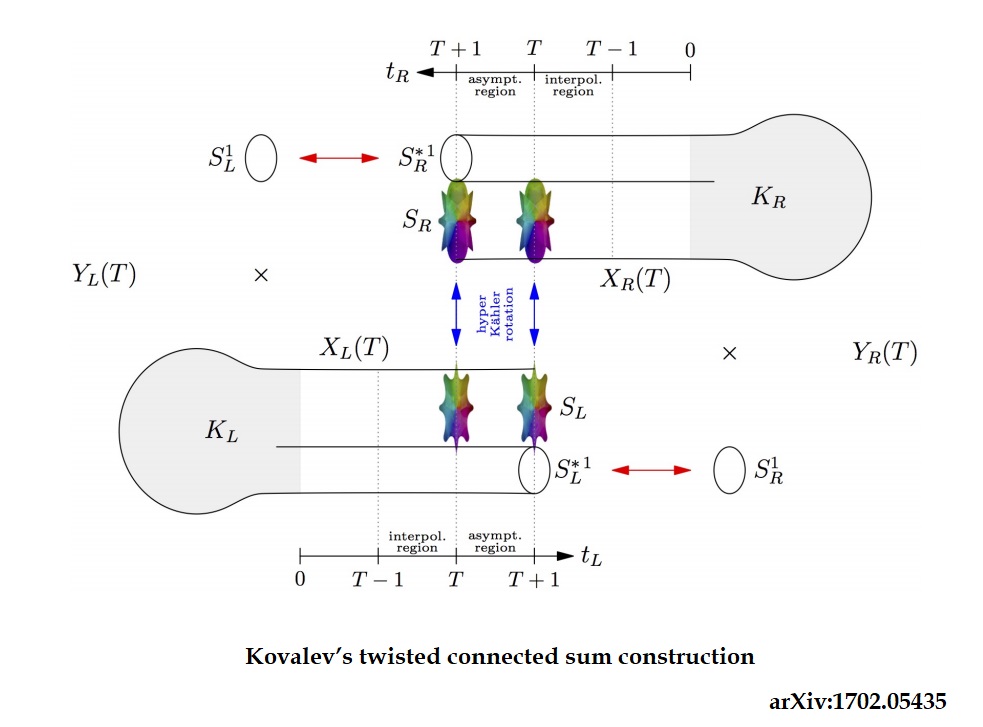
uses a dimensionally extended spacetime to 12-D that fully covariantizes supergravity under the U-duality symmetry group of M-theory. Taking full advantage of the M/F-theory duality, and Kovalev’s twisted connected sum constructed ![]() manifolds via gluing pairs of asymptotically cylindrical Calabi–Yau threefolds, M-theory is hence up to isomorphism the unique UV completion of the Standard Model of physics coupled to gravity. Moreover, by mirror symmetry, there exists an internal symmetry induced between M-theory and F-theory upon KK-reduction to Type-IIB SUGRA. Here I shall discuss singular transitions to chirality and Yukawa couplings in M-theory on Calabi-Yau manifolds that arise in the Kovalev TCS construction involving an action with half-maximal gauged supergravity:
manifolds via gluing pairs of asymptotically cylindrical Calabi–Yau threefolds, M-theory is hence up to isomorphism the unique UV completion of the Standard Model of physics coupled to gravity. Moreover, by mirror symmetry, there exists an internal symmetry induced between M-theory and F-theory upon KK-reduction to Type-IIB SUGRA. Here I shall discuss singular transitions to chirality and Yukawa couplings in M-theory on Calabi-Yau manifolds that arise in the Kovalev TCS construction involving an action with half-maximal gauged supergravity:
![]()
![]()
![]()
where we have:
![]()
![]()
![]()
with ![]() the scalar potential. In the
the scalar potential. In the ![]() formalism taking the Klebanov-Witten limit, the theory is given by the action:
formalism taking the Klebanov-Witten limit, the theory is given by the action:
![]()
where we have:
![]()
and:
![]()
and where the Chern-Simons-topological Lagrangian has covariant variational form:
![]()
with:
![]()
![]()
and the Yang-Mills field equation for the covariant field strength form ![]() is:
is:
![]()
Thus, we can derive the Chern-Simons-type topological action:
![]()
with:
![]()
and:
![]()
and the covariant curvature form ![]() and holomorphic curvature form
and holomorphic curvature form ![]() are, respectively:
are, respectively:
![]()
and:
![]()
where the Ramond-Ramond gauge-coupling sector is given by the action:
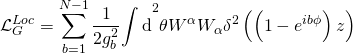
and the Ramond-Ramond term being:
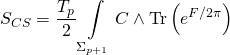
thus giving us the Type-IIB Calabi-Yau three-fold superpotential:
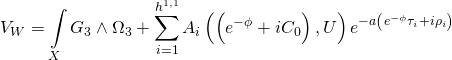
Before we can see the duality relations between M-theory and F-theory elliptically fibered Calabi-Yau Standard-Model constructions, note that the topologically mixed Yang-Mills action:
![]()
where the corresponding Chern-Simons action is:
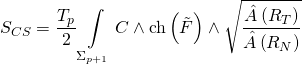
with the Ramond-Ramond coupling-term:
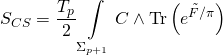
has the following variational action:
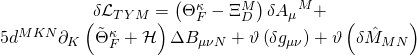
with:
![]()
![]()
![]()
![]()
Since 11-D SUGRA on a torus is equivalent to Type-IIB string-theory on a circle, the action of the modular group on the Type-IIB axio-dilaton allows us to take the zero limit of:
![]()
and by mirror symmetry, we get a Type-IIA dimensional uplift to M-theory, given that in the Einstein frame, the Type-IIB bosonic SUGRA action is:
![]()
with:
![]()
![]()
![]()
Central in EFT is the role of U-duality in the modular holomorphic action on the Neveu-Schwarz sector of Type-IIB. The generalized diffeomorphisms, generated by a vector ![]() , act locally on
, act locally on ![]() yielding the Lie derivative
yielding the Lie derivative ![]() that differs from the classic Lie derivative
that differs from the classic Lie derivative ![]() by a Calabi-Yau induced
by a Calabi-Yau induced ![]() -tensor and is implicitly defined by the transformation rules for a generalized vector:
-tensor and is implicitly defined by the transformation rules for a generalized vector:
![]()
![]()
The associated diffeomorphism algebra has an exceptional field bracket:
![]()
with closure condition:
![]()
The action diffeomorphism symmetries are parametrized by vector bundles over the metaplectic space and take the form:
![]()
with:
![]()
where the gauge vector transforms as:
![]()
The corresponding generalized exceptional scalar metric ![]() hence has the following property:
hence has the following property:
![]()
which decomposes in light of the orbifold blow-up:
![]()
as such:
![]()
thus allowing us to define the crucial exceptional metric:
![]()
Since the full Type-IIB Calabi-Yau superpotential is given by:
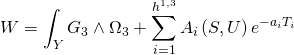
where the Kähler Type-IIB orientifold moduli is:
![]()
with:
![]()
and the volume of the divisor, ![]() , is:
, is:
![]()
with:
![]()
we now hence have the ingredients to write the modular exceptional field theory action as:
![]()
with the exceptional Ricci scalar:
![]()
![]()
the kinetic part:
![]()
![]()
and the gauge term:
![]()
![]()
and the 10+3-D Chern-Simons topological term:
![]()
![]()
![]()
where the potential has the form:
![]()
![]()
![]()
![]()
![]()
![]()
This is a theory dynamically equivalent to 11-D SUGRA and Type-IIB under the covariantized U-duality group-action. However, the gauged kinetic terms ![]() corresponding to the gauge form
corresponding to the gauge form ![]() appears only topologically in:
appears only topologically in:
![]()
![]()
![]()
Hence, the EoM for the field ![]() is given by:
is given by:
![]()
Since exceptional field theory based on the modular group ![]() uses a dimensionally extended spacetime to 12-D that fully covariantizes supergravity under the U-duality symmetry groups of M-theory, homological mirror symmetry entails the existence of an internal symmetry induced between M-theory and F-theory upon dimensional-reduction to Type-IIB SUGRA which, in the
uses a dimensionally extended spacetime to 12-D that fully covariantizes supergravity under the U-duality symmetry groups of M-theory, homological mirror symmetry entails the existence of an internal symmetry induced between M-theory and F-theory upon dimensional-reduction to Type-IIB SUGRA which, in the ![]() formalism, taking the Klebanov-Witten limit, is defined by the action:
formalism, taking the Klebanov-Witten limit, is defined by the action:
![]()
We can now derive the dimensional reduction of M-theory on ACCY threefolds that are building blocks of twisted connected sum G2 manifolds. We begin with the two-derivative action for 11d SUGRA, unique up to isomorphism, with a pure bosonic action given as such:
![]()
admitting a quantum gauge-gravitational correction:
![]()
where we have:
![]()
We then expand the 11D fields in a dimensional reduction on a Calabi-Yau threefold ![]() on a basis of zero-modes of the Dirac-Dolbeault differential operator on the ACCY internal threefold with metric:
on a basis of zero-modes of the Dirac-Dolbeault differential operator on the ACCY internal threefold with metric:
![]()
whose external part describes a maximally symmetric spacetime. Note that the fluctuations of the internal metric ![]() are zero-modes of the Lichnerowicz operator satisfying the relations:
are zero-modes of the Lichnerowicz operator satisfying the relations:
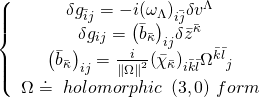
parameterized by the complex structure moduli ![]() and the Kähler moduli
and the Kähler moduli ![]() defined implicitly by the Kähler expansion:
defined implicitly by the Kähler expansion:
![]()
with the following cohomological Laplacian Calabi-Yau expansion:
![]()
and where all our fields are naturally embeddable in 5d N=2 SUSY multiplets. To see that, recall that the following identity holds:
![]()
since the total volume of our Calabi-Yau threefold is given as such:
![]()
with ![]() being the threefold Cartan-Weyl intersection numbers. Furthermore, we recall the decomposition of the third CY-cohomology into complex cohomologies:
being the threefold Cartan-Weyl intersection numbers. Furthermore, we recall the decomposition of the third CY-cohomology into complex cohomologies:
![]()
Now since we have:
![]()
the scalar fields satisfy the following relation:
![]()
leading to the natural interpretation of ![]() as 5-D holomorphic coordinates inducing a potential of the form:
as 5-D holomorphic coordinates inducing a potential of the form:
![]()
yielding the dimensionally reduced bosonic action:
![]()
![]()
with the following being a logical consequence:
![]()
In light of the threefold Cartan-Weyl intersection numbers ![]() , the elliptically fibered Calabi-Yau geometry satisfies the following relation:
, the elliptically fibered Calabi-Yau geometry satisfies the following relation:
![]()
![]()
To allow the 5D/6D lift, one defines T-shifted fields:
![]()
as required by supersymmetry, which yield the following correction to our cubic potential:
![]()
![]()
Hence, our Chern-Simons term reduces to:
![]()
![]()
![]()
with:
![]()
Hence, for M-theory on G2 TCS Kovalev manifolds with ACCY building blocks, the 4D action takes the following form:
![]()
![]()
We are now in a position to discuss Yukawa couplings and chirality. Noting that in M-theory, interactions between localized matter fields derive from M2-instantons wrapped on calibrated 3-spheres of local ALE-fibrations. Taking the G2 Higgs bundle spectral background on a 3-cycle ![]() :
:
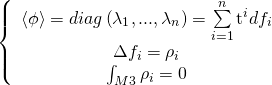
we expand the topologically twisted 7d action:
![]()
![]()
![]()
![]()
Gauge symmetry restricts matter interactions to:
![]()
determined by:
![]()
where ![]() are 1-forms that describe the bosonic ground states along the 3-cycle, and
are 1-forms that describe the bosonic ground states along the 3-cycle, and ![]() are harmonic basis. Dimensional reduction to 4D yields at all critical Morse-Witten indices a chiral multiplet
are harmonic basis. Dimensional reduction to 4D yields at all critical Morse-Witten indices a chiral multiplet ![]() in
in ![]() . Moreover, there are
. Moreover, there are ![]() chiral multiplets in
chiral multiplets in ![]() and
and ![]() derived from bulk-fields
derived from bulk-fields ![]() harmonic expansion yielding the 4D interaction term:
harmonic expansion yielding the 4D interaction term:
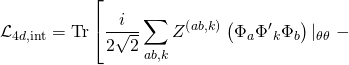
![Rendered by QuickLaTeX.com \displaystyle \left. {\frac{i}{{2\sqrt{2}}}\sum\limits_{{ab,k}}{{{{Z}^{{\left( {ab,k} \right)}}}}}\left( {{{\Phi }_{a}}{{{\tilde{\Phi }}}_{k}}{{\Phi }_{b}}} \right)\left| {_{{\theta \theta }}} \right.+\,\text{h}\text{.c}\text{.}} \right]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d77ecb88c795465e14e6a7c09340440e_l3.png)
Yukawa couplings require a rank n = 2 Higgs bundle or higher. The Morse-Witten functions:
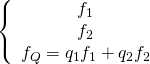
effectively yield a coupling by expanding the action:
![]()
![]()
![]()
![]()
in zero modes:
![]()
Hence, Yukawa couplings arise from M2-instantons wrapping associative three-cycle that describe ![]() ALE-fibrations over the base
ALE-fibrations over the base ![]() . M2 branes wrapped on such cycles yield the Yukawa couplings between modes hyper-localized at the critical points on the
. M2 branes wrapped on such cycles yield the Yukawa couplings between modes hyper-localized at the critical points on the ![]() ALE-fibers. The interactions are determined by the Higgs-bundle Hitchins functions
ALE-fibers. The interactions are determined by the Higgs-bundle Hitchins functions ![]() . Three-spheres supporting the Yukawa couplings are G2-manifold supersymmetric stable homology spheres determined by a superpotential class of the form:
. Three-spheres supporting the Yukawa couplings are G2-manifold supersymmetric stable homology spheres determined by a superpotential class of the form:
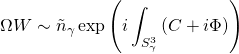
Hence, one can identify the Higgs field ![]() and the gauge field
and the gauge field ![]() with the SUGRA 3-form
with the SUGRA 3-form ![]() and the G2-associative 3-form
and the G2-associative 3-form ![]() to derive:
to derive:
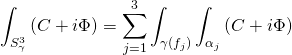
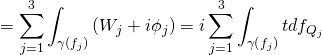
Now since the following homological relation:
![]()
holds, the superpotential assumes the following form:
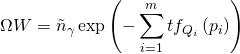
thus satisfying the SM criteria on chirality and Yukawa couplings and their associated interaction strengths.
‘Tops as Building Blocks for G2 Manifolds’ is an excellent read on M-theory on manifolds of G2 holonomy that serves to support the main claims of this post. Below is a visualization of a Kovalev TCS construction: