Orbifold compactifications of 11-D SUGRA induce ![]() exceptional symmetries in
exceptional symmetries in ![]() that are realized as U-duality symmetries of M-theory upon Z-discretization and without Betti-truncations. Therefore, exceptional field theory based on the modular group
that are realized as U-duality symmetries of M-theory upon Z-discretization and without Betti-truncations. Therefore, exceptional field theory based on the modular group ![]() utilizes a dimensionally extended spacetime to 12-D fully covariantizing SUGRA under the U-duality symmetry groups of M-theory. Homological mirror symmetry hence induces an internal symmetry between M-theory and F-theory upon KK-reduction to Type-IIB SUGRA. In the
utilizes a dimensionally extended spacetime to 12-D fully covariantizing SUGRA under the U-duality symmetry groups of M-theory. Homological mirror symmetry hence induces an internal symmetry between M-theory and F-theory upon KK-reduction to Type-IIB SUGRA. In the ![]() Witten limit, the action is given as such:
Witten limit, the action is given as such:
![]()
with:
![]()
and:
![]()
where the Chern-Simons-topological Lagrangian has covariant variational form:
![]()
with:
![]()
![]()
and the Yang-Mills field equation for the covariant field strength ![]() is given by:
is given by:
![]()
Hence, we can derive the Chern-Simons-type topological action:
![]()
with:
![]()
and:
![]()
and the covariant curvature form ![]() and holomorphic curvature form
and holomorphic curvature form ![]() are, respectively:
are, respectively:
![]()
and:
![]()
where the Ramond-Ramond gauge-coupling sector is given by the action:
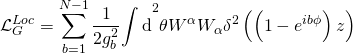
and the Ramond-Ramond term being:
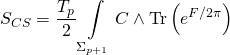
thus giving us the Type-IIB Calabi-Yau three-fold superpotential:
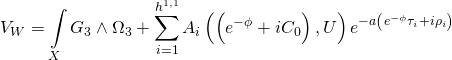
Note that the topologically mixed Yang-Mills action:
![]()
where the corresponding Chern-Simons action is:
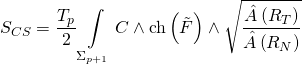
with the Ramond-Ramond coupling-term:
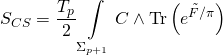
has variational action:
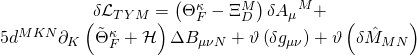
with:
![]()
![]()
![]()
![]()
Since 11-D SUGRA on a torus is equivalent to Type-IIB string-theory on a circle, the action of the modular group on the Type-IIB axio-dilaton allows us to take the zero limit of:
![]()
and by homological mirror symmetry, we get a Type-IIA dimensional uplift to M-theory, given that in the Einstein frame, the Type-IIB bosonic SUGRA action is:
![]()
with:
![]()
![]()
![]()
One can appreciate then that the essence of Exceptional Field Theory is that it characterizes a deeper double duality relating M-theory/Type-IIA and F-theory/Type-IIB. The key is the role of U-duality in the modular holomorphic action on the Neveu-Schwarz sector of Type-IIB string-theory. The generalized diffeomorphisms generated by a vector ![]() act fully locally on
act fully locally on ![]() yielding the Lie derivative
yielding the Lie derivative ![]() that differs from the classic Lie derivative
that differs from the classic Lie derivative ![]() by a Calabi-Yau induced
by a Calabi-Yau induced ![]() -tensor and is defined by the following transformation rules:
-tensor and is defined by the following transformation rules:
![]()
![]()
The corresponding diffeomorphism algebra has an exceptional field bracket:
![]()
with closure condition:
![]()
The action of the diffeomorphism-symmetries are parametrized by vector bundles over the metaplectic space and take the form:
![]()
with:
![]()
where the gauge vector transforms as:
![]()
The corresponding generalized exceptional scalar metric ![]() satisfies the following property:
satisfies the following property:
![]()
which decomposes in light of the orbifold blow-up:
![]()
as:
![]()
Hence, we can define the exceptional metric:
![]()
Since the full Type-IIB Calabi-Yau superpotential is given by:
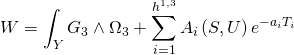
with Kähler Type-IIB orientifold moduli:
![]()
and:
![]()
and where the volume of the divisor, ![]() , is:
, is:
![]()
with:
![]()
we thus have the ingredients to write the modular exceptional field theory action as:
![]()
with the exceptional Ricci scalar:
![]()
the kinetic part:
![]()
and the gauge term:
![]()
and the 10+3-D Chern-Simons topological term:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{\mathcal{L}}_{{top}}}=\kappa \int{{{{d}^{{10}}}}}x{{d}^{3}}Y{{\varepsilon }^{{{{\mu }_{1}}...{{\mu }_{{10}}}}}}\frac{1}{4}{{\varepsilon }_{{\alpha \beta }}}{{\varepsilon }_{{\gamma \delta }}}\left[ {\frac{1}{5}} \right.{{\partial }_{s}}{{\Omega }_{{{{\mu }_{1}}...{{\mu }_{5}}}}}^{{\alpha \beta ss}}\\{{\Omega }_{{{{\mu }_{6}}...{{\mu }_{{10}}}}}}^{{\gamma \delta ss}}-\frac{5}{2}{{\Gamma }_{{{{\mu }_{1}}{{\mu }_{2}}}}}^{s}{{J}_{{{{\mu }_{3}}...{{\mu }_{6}}}}}^{{\alpha \beta s}}{{J}_{{{{\mu }_{7}}...{{\mu }_{{10}}}}}}^{{\gamma \delta }}\\+\frac{{10}}{3}2{{\Omega }_{{{{\mu }_{1}}...{{\mu }_{3}}}}}^{{\alpha s}}{{\Omega }_{{{{\mu }_{4}}...{{\mu }_{6}}}}}^{{\beta s}}\left. {{{J}_{{{{\mu }_{7}}...{{\mu }_{{10}}}}}}^{{\gamma \delta }}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c40521079942e78090ce506ff0858fb8_l3.png)
where the potential has the form:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}V=\frac{1}{4}{{\wp }^{{ss}}}\left( {{{\partial }_{s}}{{\Omega }^{{\alpha \beta }}}{{\partial }_{s}}{{\Omega }_{{\alpha \beta }}}+{{\partial }_{s}}{{g}^{{\mu \nu }}}{{\partial }_{s}}{{g}_{{\mu \nu }}}+{{\partial }_{s}}\text{In}g{{\partial }_{s}}\text{In}g} \right)\\+\frac{9}{{32}}{{\wp }^{{ss}}}{{\partial }_{s}}\text{In}{{\wp }_{{ss}}}{{\partial }_{s}}\text{In}{{\wp }_{{ss}}}-\frac{1}{2}{{\wp }^{{ss}}}{{\partial }_{s}}\text{In}{{\wp }_{{ss}}}\text{In}g\\+\wp _{{ss}}^{{3/4}}\left[ {\frac{1}{4}} \right.{{\Omega }^{{\alpha \beta }}}{{\partial }_{\alpha }}{{\Omega }^{{\gamma \delta }}}{{\partial }_{\beta }}{{\Omega }_{{\gamma \delta }}}+\frac{1}{2}{{\Omega }^{{\alpha \beta }}}{{\partial }_{\alpha }}{{\Omega }^{{\gamma \delta }}}{{\partial }_{\gamma }}{{\Omega }_{{\delta \beta }}}\\+{{\partial }_{\alpha }}{{\Omega }^{{\alpha \beta }}}{{\partial }_{\beta }}\text{In}\left( {{{g}^{{1/2}}}\wp _{{ss}}^{{3/4}}} \right)+\\\frac{1}{4}{{\Omega }^{{\alpha \beta }}}\left( {{{\partial }_{\alpha }}} \right.{{g}^{{\mu \nu }}}{{\partial }_{\beta }}{{g}_{{\mu \nu }}}+{{\partial }_{\alpha }}\text{Ing}{{\partial }_{\beta }}\text{In}g+\frac{1}{4}{{\partial }_{\alpha }}\text{In}{{\wp }_{{ss}}}{{\partial }_{\beta }}\text{In}{{\wp }_{{ss}}}\\+\left. {\frac{1}{2}\left. {{{\partial }_{\alpha }}\text{In}g{{\partial }_{\beta }}\text{In}{{\wp }_{{ss}}}} \right)} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-11e43105f09fb46e9bcbc0863bfedc10_l3.png)
Essentially, we have deduced a theory that is dynamically equivalent to 11-D SUGRA and Type-IIB under the covariantized U-duality group-action. However, the gauged kinetic terms ![]() corresponding to the gauge form
corresponding to the gauge form ![]() appear only topologically in:
appear only topologically in:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{*{20}{l}} {{{\mathcal{L}}_{{top}}}=\kappa \int{{{{d}^{{10}}}}}x{{d}^{3}}Y{{\varepsilon }^{{{{\mu }_{1}}...{{\mu }_{{10}}}}}}\frac{1}{4}{{\varepsilon }_{{\alpha \beta }}}{{\varepsilon }_{{\gamma \delta }}}\left[ {\frac{1}{5}} \right.{{\partial }_{s}}{{\Omega }_{{{{\mu }_{1}}...{{\mu }_{5}}}}}^{{\alpha \beta ss}}} \\ {{{\Omega }_{{{{\mu }_{6}}...{{\mu }_{{10}}}}}}^{{\gamma \delta ss}}-\frac{5}{2}{{\Gamma }_{{{{\mu }_{1}}{{\mu }_{2}}}}}^{s}{{J}_{{{{\mu }_{3}}...{{\mu }_{6}}}}}^{{\alpha \beta s}}{{J}_{{{{\mu }_{7}}...{{\mu }_{{10}}}}}}^{{\gamma \delta }}} \\ {+\frac{{10}}{3}2{{\Omega }_{{{{\mu }_{1}}...{{\mu }_{3}}}}}^{{\alpha s}}{{\Omega }_{{{{\mu }_{4}}...{{\mu }_{6}}}}}^{{\beta s}}\left. {{{J}_{{{{\mu }_{7}}...{{\mu }_{{10}}}}}}^{{\gamma \delta }}} \right]} \end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-af47b800b5a7cb95241241c56fa9d29c_l3.png)
Hence, the EoM for the field ![]() are given as such:
are given as such:
![]()
By U-duality, homological mirror symmetry then entails an internal symmetry between M-theory and F-theory upon dimensional-reduction to Type-IIB SUGRA, which in the ![]() formalism, taking the Klebanov-Witten limit, is defined by the action:
formalism, taking the Klebanov-Witten limit, is defined by the action:
![]()
Let us delve deeper into this M/F-U-duality, noting that it is a duality that is rich in F-theory phenomenology, and by the Type-IIB duality, such phenomenology is inherited by 11-D SUGRA under U-duality. First note that ![]() -EFT is equivalent to both, 11-D SUGRA and Type-IIB SUGRA. The field content for EFT consists of:
-EFT is equivalent to both, 11-D SUGRA and Type-IIB SUGRA. The field content for EFT consists of:
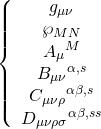
whereas the field content for M-theory consists of:
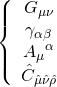
while that of Type-IIB is given by:
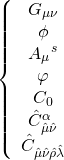
The Kaluza-Klein and gauge fields for M-theory are, respectively:
![]()
![]()
![]()
and:
![]()
![]()
![]()
For the split-Type-IIB theory, the Kaluza-Klein and gauge fields are respectively:
![]()
![]()
![]()
where we have:
![]()
and we parametrize ![]() in terms of the axio-dilaton
in terms of the axio-dilaton ![]() as such:
as such:
![]()
The ![]() -EFT/11-D/Type-IIB duality can now be formulated in terms of the gauge field equations as such:
-EFT/11-D/Type-IIB duality can now be formulated in terms of the gauge field equations as such:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{C}_{{\mu \nu \rho }}}^{{\alpha \beta ,s}}={{\varepsilon }^{{\alpha \beta }}}{{{\hat{C}}}_{{\mu \nu \rho s}}}+3{{{\hat{C}}}_{{\left[ {\left. \mu \right|\left. s \right|} \right.}}}^{{\left[ \alpha \right.}}{{C}_{{\left. {\nu \rho } \right]}}}^{{\left. \beta \right]}}\\-2{{{\hat{C}}}_{{\left[ {\left. \mu \right|s} \right.}}}^{\alpha }{{{\hat{C}}}_{{\left. \nu \right|\left. s \right|}}}^{\beta }{{A}_{{\left. \rho \right]}}}^{s}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-252ac42ab1bbdde2c8c3bb805ae56ae3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{D}_{{\mu \nu \rho \sigma }}}^{{\alpha \beta ,ss}}={{\varepsilon }^{{\alpha \beta }}}\left( {{{{\hat{C}}}_{{\mu \nu \rho \sigma }}}+4{{A}_{{\left[ \mu \right.}}}^{s}{{{\hat{C}}}_{{\left. {\nu \rho \sigma } \right]s}}}} \right)\\+6{{{\hat{C}}}_{{\left[ {\mu \nu } \right.}}}^{{\left[ \alpha \right.}}{{{\hat{C}}}_{{\rho \left| s \right|}}}^{{\left. \beta \right]}}{{A}_{{\left. \sigma \right]}}}^{s}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-44dd55d1d565a93396ba04cf4658051f_l3.png)
Hence we can now define F-theory as the modular equivariant 12-D lift of Type-IIB with varying axio-dilaton and 7-brane geometric backreaction where the ![]() duality U-action yields a monodromy-group representation induced by elliptic fibrations that admit a duality with M-theory via KK-reduction. The
duality U-action yields a monodromy-group representation induced by elliptic fibrations that admit a duality with M-theory via KK-reduction. The ![]() -EFT diffeomorphism group action has two Sen singularity solutions, one corresponding to F-theory, one to 11-D SUGRA. Hence, such a 12-D field theory dimensionally reduces in the Witten-Vafa limit, to 11-D SUGRA and 10-D Type-IIB.
-EFT diffeomorphism group action has two Sen singularity solutions, one corresponding to F-theory, one to 11-D SUGRA. Hence, such a 12-D field theory dimensionally reduces in the Witten-Vafa limit, to 11-D SUGRA and 10-D Type-IIB.
Since the D7-brane backreaction is central to F-theory, let’s study it under the ![]() -EFT/11-D/Type-IIB duality. Solutions to the D7-brane worldvolume action in Type-IIB SUGRA possess non-trivial axio-dilaton and metric. Let a D7-brane extend along the six-dimensions of the internal manifold in the
-EFT/11-D/Type-IIB duality. Solutions to the D7-brane worldvolume action in Type-IIB SUGRA possess non-trivial axio-dilaton and metric. Let a D7-brane extend along the six-dimensions of the internal manifold in the ![]() and
and ![]() directions, and we represent the time direction transverse to the brane in polar coordinates
directions, and we represent the time direction transverse to the brane in polar coordinates ![]() . Thus, the harmonic functional of the D7-brane is
. Thus, the harmonic functional of the D7-brane is ![]() and the solutions to our system are given by:
and the solutions to our system are given by:
![]()
![]()
![]()
![]()
Holomorphically circling the transverse dimension yields, by the monodromy group action on ![]() ,
, ![]() :
:
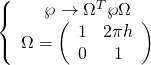
The D7-brane solution is derived via Type-IIB dimensional reduction under the elliptic fibrational structure underlying the monodromy action on the CY fourfold geometry:
![]()
![]()
![]()
On the M-section, we have a monopole-smearing solution:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}\text{d}s_{{\left( {11} \right)}}^{2}=-\text{d}{{t}^{2}}+\text{d}\overrightarrow{{x_{{\left( 6 \right)}}^{2}}}+H\left( {\text{d}{{r}^{2}}+{{r}^{2}}\text{d}{{\theta }^{2}}+{{{\left( {\text{d}{{y}^{1}}} \right)}}^{2}}} \right)\\+{{H}^{{-1}}}{{\left[ {\text{d}{{y}^{2}}+h\theta \text{d}{{y}^{1}}} \right]}^{2}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-68f3812e3228f6d88ad2c388035a7440_l3.png)
Hence, by the M/Type-IIB duality (via F-theory), the smearing relates the first Chern class of the Witten-Vafa fibration to the co-dimension two monodromy hypercharges. By modularity, the D7-brane hyperdoublet and the D3-brane multiplet are smeared monopoles that p-q-7-branes in Type-IIB with p-cycles and q-cycles holomorphically wrap. The metric of a p-q-Type-IIB theory is given as such:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c}\text{d}s_{{\left( 3 \right)}}^{2}=\frac{{{{H}^{{-1}}}}}{{{{p}^{2}}+{{q}^{2}}}}\left\{ {\left[ {{{p}^{2}}{{H}^{2}}+{{{\left( {ph\theta -q} \right)}}^{2}}} \right]{{{\left( {\text{d}{{y}^{1}}} \right)}}^{2}}} \right.\\+\left[ {{{{\left( {p+qh\theta } \right)}}^{2}}+{{q}^{2}}{{H}^{2}}} \right]{{\left( {\text{d}{{y}^{2}}} \right)}^{2}}\\-2\left[ {\left( {{{p}^{2}}-{{q}^{2}}} \right)h\theta +pq\left( {K-1} \right)} \right]\left. {\text{d}{{y}^{1}}\text{d}{{y}^{2}}} \right\}+{{\left( {{{\text{d}}^{s}}} \right)}^{2}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-466888942f19045d9c7c365a90a61ae6_l3.png)
Thus, the exceptionality property determines two holomorphic functions ![]() and
and ![]() where the modulus takes the form:
where the modulus takes the form:
![]()
with elliptic invariant Jacobian. The polynomial roots give rise to Type-IIB singularities localizing the 7-branes. Hence we get:
![]()
and for the M-section, we have:
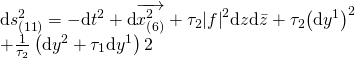
Both maintain the elliptic fibrational base singularities under which the action of the M/Type-IIB duality symmetry gives rise to generalized Klebanov-Witten quiver gauge theories that yield the Yang-Mills gauge theories of the Standard Model. Exceptionality hence eliminates the need to go to the full-blown 12-D F-theory and thus eliminates both, Betti-truncations and the KK-conical blow-up sector that otherwise would have to be Higgsed away upon dimensional reduction to 11-D SUGRA. This is phenomenologically central in deriving the Standard Model of physics from F-theory, and hence M-theory in light of the M/F-theory duality.