String-string duality entails an equivalence between the membrane action corresponding to ![]() and the
and the ![]() orbifold action of
orbifold action of ![]() . Which entails a deep relation between string-string duality and the action of M2/5-branes, a few implications of which are my focus here.
. Which entails a deep relation between string-string duality and the action of M2/5-branes, a few implications of which are my focus here.
The bosonic sector membrane action is given by:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{S = {S_M} + \int_{\partial {M^3}} {\left\{ {\frac{1}{2}} \right.} \left( {{g_{mn}}{\eta ^{ij}} + {b_{mn}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^m}{\partial _j}{x^n} + \frac{1}{2}\left( {{g_{IJ}}{\eta ^{ij}} + {b_{IJ}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^I}{\partial _j}{x^J} + {\varepsilon ^{ij}}{\partial _i}{x^J}{\partial _j}{x^m}\left. {A_m^J(x)} \right\}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4882eceed14877eb1333bb4a24c24503_l3.png)
where:
![]()
Now, recall that I derived the total action:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S^{T}} = \frac{1}{{2\pi {\alpha ^\dagger }12}}\int\limits_{{\rm{world - volumes}}} {{d^{26}}} x\,d\,\Omega {\left( {{\phi _{inst}}} \right)^2}\sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} \,{e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}} \cdot \\\left( {{R_{icci}} - 4{{\left( {{{\not D}^{susy}}\left( {{\phi _{inst}}} \right)} \right)}^2}} \right) + \frac{1}{{12}}H_{3,\mu \nu \lambda }^bH_3^{b,\mu \nu \lambda }/A_\mu ^H + \sum\limits_{D - p - branes} {S_{Dp}^{WV}} \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-452301a9de070e4bc6e9d7128ca1ad99_l3.png)
which is highly non-trivial since Clifford algebras are metaplectic quantizations of exterior algebras. Applying piece-wise to the Poincaré line bundle, we get by Gaussian matrix elimination, an expansion of ![]() via Green’s function, yielding the on-shell action of M-theory in the Witten gauge:
via Green’s function, yielding the on-shell action of M-theory in the Witten gauge:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_M} = \frac{1}{{{k^9}}}\int\limits_{{\rm{world - volumes}}} {{d^{11}}} \sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} {T_p}^{10}d\Omega {\left( {{\phi _{inst}}} \right)^{26}}\left( {{R_{icci}} - A_\mu ^H\frac{1}{{48}}G_4^2} \right) + \\\sum\limits_{Dp} {D_\mu ^{susy}} {e^{ - H_3^b}}/S_{Dp}^{WV} + \sum\limits_{Dp} {D_\nu ^{susy}} {e^{H_3^b}}/S_{Dp}^{SV}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1a0ae0e886994172b2227819ca6950f2_l3.png)
with ![]() the kappa symmetry term,
the kappa symmetry term, ![]() the metric on
the metric on ![]() , and
, and ![]() the corresponding coordinates with
the corresponding coordinates with ![]() an antisymmetric 3-tensor. Hence, the worldvolume
an antisymmetric 3-tensor. Hence, the worldvolume ![]() is:
is:
![]()
and where the Hamiltonian metaplectic action in the Heisenberg representation on the Dp+1 dimensional worldspaces gives us:
![]()
where:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\Im _i} = - \not \partial {\phi _{si}}{T_{Dp}}d\,\Omega {{({\phi _{si}})}^{2\pi ik}}}\\{\not K = - {{\not \partial }_i}{{\widetilde E}^i} + {{( - 1)}^{p + 1}}{T_{Dp}}{S^{{\rm{Fer}}}}}\\{{{\not H}_i} = \widetilde P{\alpha _i}\widetilde E_i^\alpha {{\not \partial }_i}{\phi _{si}} + \widetilde E{{\not F}_{ij}}}\\{H = \frac{1}{{2\pi ik}}\left[ {{{\widetilde P}^2} + {{\widetilde E}^i}{{\widetilde E}^j}{G_{ij}} + T_{Dp}^2{e^{ - 2{\phi _{si}}}}{\rm{det}}\left( {{G_{ij}} + {{\not F}_{ij}}} \right)} \right]}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bd828556ea51b8c78862eb753658693f_l3.png)
with:
![]()
and:
![]()
The bosonic sector hence lives on the boundary of the open membrane. Two copies of ![]() naturally couple to the U(1) connections
naturally couple to the U(1) connections ![]() .
.
Now, double dimensional reduction of the twisted supermembrane on:
![]()
of
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{S = {S_M} + \int_{\partial {M^3}} {\left\{ {\frac{1}{2}} \right.} \left( {{g_{mn}}{\eta ^{ij}} + {b_{mn}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^m}{\partial _j}{x^n} + \frac{1}{2}\left( {{g_{IJ}}{\eta ^{ij}} + {b_{IJ}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^I}{\partial _j}{x^J} + {\varepsilon ^{ij}}{\partial _i}{x^J}{\partial _j}{x^m}\left. {A_m^J(x)} \right\}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4882eceed14877eb1333bb4a24c24503_l3.png)
entails that the bosonic sector is that of the heterotic string:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{{S_h}\int {{d^2}} \sigma \left\{ {\frac{1}{2}} \right.\left( {{g_{mn}}{\eta ^{ij}} + {b_{mn}}{\varepsilon ^{ij}}} \right){\partial _i}{x^m}{\partial _j}{x^n}}\\{ + \frac{1}{2}\left( {{g_{IJ}}{\eta ^{ij}} + {b_{IJ}}{\varepsilon ^{ij}}} \right){\partial _i}{x^I}{\partial _j}{x^I} + }\\{{\varepsilon ^{ij}}{\partial _i}{x^I}{\partial _n}{x^m}\left. {A_m^{(I)}(x)} \right\}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d29fbffef61d22da311051a09bec0ceb_l3.png)
with gauge group indices I = 1, … , 16, where general Dp-brane solutions, p = 1, 2, 3, 4 preserving 1/2 SUSY, are of the general form:
![]()
![]()
![]()
![]()
and where the M5-brane action in a D = 11 SUGRA background is given by:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=2\int_{{{{M}_{6}}}}{{d{{x}^{6}}}}\left[ {\sqrt{{-\det \left( {{{g}_{{\mu \nu }}}+i{{{\tilde{H}}}_{{\mu \nu }}}} \right)}}} \right.\\+\frac{{\sqrt{{-g}}}}{{4{{{\left( {\partial a} \right)}}^{2}}}}{{\partial }_{\lambda }}a{{{\tilde{H}}}^{{\lambda \mu \nu }}}\left. {{{H}_{{\mu \nu \rho }}}{{\partial }^{\rho }}_{a}} \right]-\int_{{{{M}_{6}}}}{{{{C}_{6}}}}+{{H}_{3}}\wedge {{C}_{3}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f2a7df4d5552e0c092ce01b23b22cfbe_l3.png)
with:
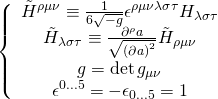
and the ![]()
![]() Lagrangian is:
Lagrangian is:
![]()
with covariant derivative given by:
![]()
and the Chern-Simons term is:
![]()
Now consider:
![]()
with dimension:
![]()
Since the worldsheet action:
![]()
is now just a sum of three terms:
![]()
![]()
![]()
and the index I = 1, … , 22 labels 22 gauge fields, 16 coming from the internal dimensions of the heterotic string, and the other 6 gauge fields are the KK modes of the metric and antisymmetric tensor, the action ![]() then has a massless spectrum given by moduli fields corresponding to deformations of the Narain lattice and thus take values in the group manifold:
then has a massless spectrum given by moduli fields corresponding to deformations of the Narain lattice and thus take values in the group manifold:
![]()
Something fundamentally deep has occurred: all the gauge fields of the action 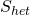 have appeared within a two-dimensional theory, and not a three-dimensional theory
have appeared within a two-dimensional theory, and not a three-dimensional theory
This is precisely the long wavelength limit behavior of the open membrane:
the gauge fields are defined in terms of fields which live on 10-dimensional boundaries of M-solutions with natural interpretation as product-spaces of multi-centered Taub-NUT solutions and EFCY fourfolds divided by the orbifold action of Type-II-B 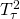 Hitchin fibrations
Hitchin fibrations
In the closed membrane case, the gauge fields are defined in terms of 11-dimensional fields.
Hence, the gauge fields of the closed membrane must be defined over M3 and not over its boundary, unlike the open membrane, whose action on  is
is
![]()
where ![]() is
is ![]() with the spacetime being
with the spacetime being ![]() .
.
Hence, the closed membrane action ![]() on
on ![]() reduces to:
reduces to:
![]()
with:
![]()
and
![]()
and since ![]() surfaces have no one-cycles, it follows that the 3-form potential that appears in
surfaces have no one-cycles, it follows that the 3-form potential that appears in ![]() appears in the action:
appears in the action:
![]()
and the ![]() -brane action takes the following form:
-brane action takes the following form:
![]()
where
![]()
with:
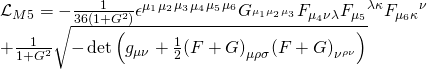
Thus, the 3-form can be expanded in terms of the cocycles of ![]() .
.
For the 22 2-cocycles of ![]() , one can decompose
, one can decompose ![]() in a similar way for the 2-form potential:
in a similar way for the 2-form potential:
![]()
with I = 1, …, 22 labeling the two-cycles of ![]() . After insertion into
. After insertion into ![]() , we can derive:
, we can derive:
![]()
Applying reparametrization invariance, we can set:
![]()
where ![]() is a worldvolume coordinate, and now we perform a dimensional reduction of:
is a worldvolume coordinate, and now we perform a dimensional reduction of:
![]()
Here are the key propositions relevant to the membrane/string duality of the low energy theory in D=7.
- the kinetic terms for the gauge fields in D=7 supergravity are:
![]()
derived by a split of the 4-4 field strength ![]() , of the 11-dimensional supergravity action:
, of the 11-dimensional supergravity action:
![]()
from the following term:
![]()
- Membrane/string duality in D=7 requires the existence of a point in the moduli space where all the 22 gauge fields are enhanced via U(1) gauging: this is key to preserving kappa symmetry. Thus, at the point in the moduli space when the 22 two-cycles vanish the following holds:
![]()
- Hence, dimensional reduction yields:
![]()
So, the S-duality map:
![]()
takes:
![]()
to:
![]()
and is equivalent to the term ![]() in:
in:
![]()
So, the above map acts on the induced metric of the worldvolume. It follows then that the B-term in:
![]()
yields, after a double dimensional reduction of ![]() , the following:
, the following:
![]()
with:
![]()
which yields an equivalence between:
![]()
and
![]()
Thus, the S-duality map that takes ![]() to
to ![]() also takes
also takes ![]() to the dimensionally reduced
to the dimensionally reduced ![]() .
.
To achieve the matching of gauge sectors of the closed and open membrane, we must generate the gauge fields of the closed membrane before dimensionally reducing the theory, as opposed to the gauge fields of the open membrane, which are always generated within the two-dimensional theory. This explains the origin of strong-weak duality in string theory. The strong coupling limit of type IIA is 11-dimensional supergravity which arises as the long wavelength limit of M-theory. So, gauge fields present in the 3-dimensional theory will be strongly interacting, and will continue to be strongly interacting after dimensional reduction to a two-dimensional theory. However, the open membrane has its gauge fields appearing in two dimensional theories, which are therefore weakly interacting.
So, we must consider the spacetime part of the action for the closed membrane:
![]()
The term:
![]()
can be dimensionally reduced to:
![]()
which is equivalent to the first term in:
![]()
and the term:
![]()
maps to:
![]()
with ![]() and
and ![]() members of
members of ![]() .
.
Now, since the term is topological, and S-duality entails:
![]()
we can then reduce:
![]()
to:
![]()
with ![]() the Hodge dual, which in turn allows us to further reduce to:
the Hodge dual, which in turn allows us to further reduce to:
![]()
Therefore the b-term in the spacetime string action is a direct consequence of the duality of the seven dimensional duality between 3- and 4-forms, and so the dimensional reduction of 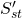 yields the term
yields the term 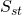 , and this is tantamount to mapping the closed membrane action on
, and this is tantamount to mapping the closed membrane action on 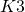 to the open membrane action on
to the open membrane action on 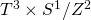 , thus D=6 string-string duality follows and both theories will have the same spacetime supersymmetry since they have the same massless spectra
, thus D=6 string-string duality follows and both theories will have the same spacetime supersymmetry since they have the same massless spectra
This naturally brings us to the connection between string field theory and Dp-branes. Recall that one derives the string propagator by an evaluation of the Witten supersymmetric quantum path integral on a fiber-strip with the Polyakov string action:
![]()
with:
![]()
for ![]() and the Regge parameter clear from context. In the proper-time gauge and the normal modes of the lapse and shift functions in 2-D, the Polyakov metric has the following property:
and the Regge parameter clear from context. In the proper-time gauge and the normal modes of the lapse and shift functions in 2-D, the Polyakov metric has the following property:
![]()
allowing us to derive the open string field Polyakov propagator corresponding to Dp-branes:
![Rendered by QuickLaTeX.com \[\begin{array}{c}G\left[ {{X_1};{X_2}} \right) = \int_0^\infty {ds} \left\langle {{X_1}\left| {\exp \left[ { - is\left( {{L_0} - i\tilde \varepsilon } \right)} \right]} \right|{X_2}} \right\rangle \\ = \left\langle {{X_1}\left| {\frac{1}{{{L_0} - i\tilde \varepsilon }}} \right|{X_2}} \right\rangle \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-89438f647f490708cfa6e25a36fb1a7c_l3.png)
with:
![]()
and the momentum operators are given by:
![Rendered by QuickLaTeX.com \[{P^\mu }\left( \sigma \right) = \frac{1}{\pi }{\left( {{p^\mu } + \sqrt 2 \sum\limits_{n = 1} {p_n^\mu \cos \left( {n\sigma } \right)} } \right)_{,\mu = 0,1,...,d}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-19aa95d541a432d36912934ee4da0545_l3.png)
![]()
Since open string end-points are topologically glued to ![]() Dp-branes, open strings must have
Dp-branes, open strings must have ![]() inequivalent quantum states and thus, the string field
inequivalent quantum states and thus, the string field ![]() has to carry the gauge group indices of
has to carry the gauge group indices of ![]() :
:
![]()
where ![]() are the generators of the SU(N) group, with
are the generators of the SU(N) group, with ![]() . Hence, the string propagator on multi-Dp-branes takes the following form, with contraction and indices ordering:
. Hence, the string propagator on multi-Dp-branes takes the following form, with contraction and indices ordering:
![]()
which yields the field theory action:
![]()
BRST-invariantly as:
![]()
Hence, the above field theory action implies that the string-string duality associates to every Dp–Brane a solution corresponding to the d–dimensional string–frame Lagrangian:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{\mathcal{L}_{S,d}} = \sqrt {\left| g \right|} \left\{ {{e^{ - 2\phi }}} \right.\left[ {R - 4{{\left( {\partial \phi } \right)}^2}} \right] + \\\frac{{{{( - )}^{p + 1}}}}{{2\left( {p + 2} \right)!}}{e^{a\phi }}\left. {F_{\left( {p + 2} \right)}^2} \right\}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e595d8bd49324003a7101ba1a1a1a8fb_l3.png)
with ![]() the dilaton,
the dilaton, ![]() the curvature of a (p + 1)–form gauge field:
the curvature of a (p + 1)–form gauge field:
![]()
where the two–index NS-NS tensor ![]() and the dual six-index heterotic five–brane tensor
and the dual six-index heterotic five–brane tensor ![]() are given by:
are given by:
![]()
and
![]()
Now we have the general form of a 10-D p-brane solution:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{ds_{S,d}^2 = {H^\alpha }dx_{\left( {p + 1} \right)}^2 - {H^\beta }dx_{\left( {D - p - 1} \right)}^2}\\{{e^{2\phi }} = {H^\gamma }}\\{{F_{0...pi}} = \delta {\partial _i}{H^{\tilde \varepsilon }}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2289bec5801dc6befb29272db1a7515b_l3.png)
with:
![]()
and:
![]()
with
![]()
The general form of 11-D M–brane solutions, noting the absence of the dilaton field, with the following Lagrangian:
![Rendered by QuickLaTeX.com \[{\mathcal{L}_{Ein,d}} = \sqrt {\left| g \right|} \left[ {R + \frac{1}{2}{{\left( {\partial \phi } \right)}^2} + \frac{{{{( - )}^{p + 1}}}}{{2\left( {p + 2} \right)!}}{e^{\alpha \phi }}F_{\left( {p + 2} \right)}^2} \right]\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-66fe4e93349a0e2c7ade0c36f5b8fb86_l3.png)
is:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{c}}{\alpha = - \frac{4}{N}\left( {d - p - 3} \right),}&{\beta = \frac{4}{N}\left( {p + 1} \right)}\\{\gamma = \frac{{4a}}{N}\left( {d - 2} \right),}&\begin{array}{l}{\delta ^2} = \frac{4}{N}\left( {d - 2} \right)\\\tilde \varepsilon = - 1\end{array}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5a39bda56f1832e2848d86fd66141721_l3.png)
Hence, the M2-brane solution is:
![]()
![]()
squaring the field strength gives the following M5-brane solution:
![]()
![]()
In the string-frame Ramond-Ramond gauge field Lagrangian:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{\mathcal{L}_{S,d}} = \sqrt {\left| g \right|} \left\{ {{e^{ - 2\phi }}} \right.\left[ {R - 4{{\left( {\partial \phi } \right)}^2}} \right] + \\\frac{{{{( - )}^{p + 1}}}}{{2\left( {p + 2} \right)!}}{e^{a\phi }}\left. {F_{\left( {p + 2} \right)}^2} \right\}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e595d8bd49324003a7101ba1a1a1a8fb_l3.png)
Dp-brane solutions have the following form:
![]()
![]()
![]()
where the Ramond-Ramond gauge-coupling sector is given by the action:
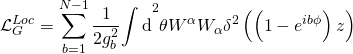
and the Ramond-Ramond term being:
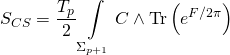
thus giving us the Type-IIB Calabi-Yau three-fold superpotential:
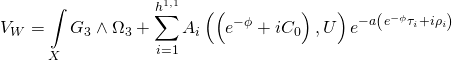
and the topologically mixed Yang-Mills action is given by:
![]()
with the corresponding Chern-Simons action:
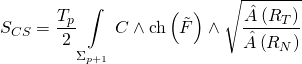
and where the Ramond-Ramond coupling-term:
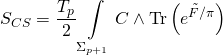
has variational action:
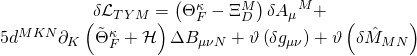
Now, from the string-string duality above and ![]() , we can derive the kinetic term of Dp–branes in terms of the Dirac-Born–Infeld action with the following form:
, we can derive the kinetic term of Dp–branes in terms of the Dirac-Born–Infeld action with the following form:
![]()
with the embedding metric and the gauge field world-volume curvature manifest, entailing the existence of a Wess-Zumino RR term that couples to Dp-branes:
![]()
![]()
and where the heterotic ![]() , the NS5-brane, and the D5–brane dual potentials are given by:
, the NS5-brane, and the D5–brane dual potentials are given by:
![]()
![]()
![]()
Parallels for the M5-brane are formally similar. We have the quadratic kinetic term:
![]()
with the WZ term:
![]()
and the dual 6–form potential:
![]()
By the field-property of the Polyakov propagator on Dp-branes:
![Rendered by QuickLaTeX.com \[\begin{array}{c}G\left[ {{X_1};{X_2}} \right) = \int_0^\infty {ds} \left\langle {{X_1}\left| {\exp \left[ { - is\left( {{L_0} - i\tilde \varepsilon } \right)} \right]} \right|{X_2}} \right\rangle \\ = \left\langle {{X_1}\left| {\frac{1}{{{L_0} - i\tilde \varepsilon }}} \right|{X_2}} \right\rangle \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-89438f647f490708cfa6e25a36fb1a7c_l3.png)
combined with string-string duality, it follows that all Dp-and-M–brane solutions preserve half of SUSY, with the SUSY rules for the gravitino and dilatino in the string-frame given by:
![]()
![]()
![]()
for IIA:
![Rendered by QuickLaTeX.com \[{{\tilde \varepsilon '}_{(p)}} = \left\{ {\begin{array}{*{20}{c}}{\tilde \varepsilon \quad \quad \quad p = 0}\\{{\gamma _{11}}\tilde \varepsilon \quad \quad \quad p = 2}\\{\tilde \varepsilon \quad \quad \quad p = 4}\\{{\gamma _{11}}\tilde \varepsilon \quad \quad \quad p = 6}\\{\tilde \varepsilon \quad \quad \quad p = 8}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-06dc318c3e8b188b2812c7af2a93372e_l3.png)
and for IIB:
![Rendered by QuickLaTeX.com \[{{\tilde \varepsilon '}_{(p)}} = \left\{ {\begin{array}{*{20}{c}}{{\rm{i}}\tilde \varepsilon \quad \quad \quad p = - 1}\\{{\rm{i}}{{\tilde \varepsilon }^ * }\quad \quad \quad p = 1}\\{{\rm{i}}\tilde \varepsilon \quad \quad \quad p = 3}\\{{\rm{i}}{{\tilde \varepsilon }^ * }\quad \quad \quad p = 5}\\{{\rm{i}}\tilde \varepsilon \quad \quad \quad p = 7}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-75d3fb8c80ebfe57d528b81dd199e149_l3.png)
where the Killing spinor is given by:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\tilde \varepsilon = {H^{ - 1/8}}{{\tilde \varepsilon }_0}}\\{\tilde \varepsilon + {\gamma _{01...p}}{{\tilde \varepsilon '}_{(p)}} = 0}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6de5f8a11c4c3034d14d37cbac832d27_l3.png)
with ![]() a constant spinor.
a constant spinor.
Hence, the triangular interplay between string-string duality, string-field theory, and the action of Dp-branes and M2/5-branes establishes a duality between 4-D Sasaki-Einstein spacetime lattices and the string-world-sheet Narain lattice, entailing the equivalence between the K-3 membrane action and the ![]() orbifold action. This has deep implications for the conformal bootstrap program in light of the Monstrous moonshine.
orbifold action. This has deep implications for the conformal bootstrap program in light of the Monstrous moonshine.
