Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

Klebanov-Strassler Warped Spacetime Geometry and M-Theoretic Cosmology

By Posted on In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Super String Theory, Supersymmetry, Time ,
photo

Loosely put: Klebanov-Strassler spacetime geometry in string-theory, is the warped product of 4-D Minkowski spacetime with 6-D Calabi-Yau orientifold

In part one, I showed, in the context of 4-D low-energy effective description of the KKLT string flux compactifications proposal, that in the limit of N = 1 supergravity, where the moduli potential {V_F} is characterized by a superpotential W and a Kähler potential {\rm K}

    \[{V_F} = {e^{{\rm K}/M_{pl}^2}}\left[ {{{\rm K}^{i\overline j }}{D_i}W\overline {{D_j}W} - \frac{1}{{M_{pl}^2}}{{\left| W \right|}^2}} \right]\]

where W is defined by

    \[\left\{ {\begin{array}{*{20}{c}}{{D_i}W \equiv {{\not \partial }_i}W + \frac{1}{{M_{pl}^2}}\left( {{{\not \partial }_i}{\rm K}} \right)W}\\{{{\rm K}_{i\overline j }} \equiv {{\not \partial }_i}{{\not \partial }_{\overline j }}{\rm K}}\end{array}} \right.\]

yields a standard Calabi-Yau compactification containing 3-form flux {G_3} \equiv {F_3} - \tau {H_3} that contributes to the superpotential via the Gukov-Vafa-Witten 4-fold term

    \[W_{{\rm{Flux}}}^{GV} = \int {{G_3}} \wedge \Omega \]

with \Omega the holomorphic 3-form on the Calabi-Yau three-fold and

    \[\tau \equiv {C_0} + i{e^{ - \Phi }}\]

is the axionic-dilaton, and the Kähler potential for the complex structure moduli and the dilaton are related as

    \[\begin{array}{c}{\rm K} = - M_{pl}^2\,{\rm{In}}\left[ {\int {\Omega \wedge \overline \Omega } } \right] - \\M_{pl}^2\,{\rm{In}}\left[ {\tau + \overline \tau } \right]\end{array}\]

and thus the KKLT-model gives us a framework for stabilizing the overall size of the compact manifold by including non-perturbative quantum effects on Dp-branes or Euclidean Dn-instantons and are parameterized via the following superpotential

    \[{W_{\pi {\rm{p}}}} = A{e^{ - a\rho }}\]

with a a constant, and that

    \[K = - 3M_{pl}^2\,{\rm{In}}\left[ {\rho + \bar \rho } \right]\]

the F-term potential in

    \[{V_F} = {e^{{\rm K}/M_{pl}^2}}\left[ {{{\rm K}^{i\overline j }}{D_i}W\overline {{D_j}W} - \frac{1}{{M_{pl}^2}}{{\left| W \right|}^2}} \right]\]

leads to a supersymmetric anti-de Sitter vacua

    \[{D_\rho }W = {D_\rho }\left( {W_{{\rm{Flux}}}^{GV} + {W_{\pi \rho }}} \right) = 0\]

with a stable Kähler modulus, leading to the deep Picard–Lefschetz-theoretic property:

the Calabi-Yau compactification is stabilized at large volume

{\rho _ * } \gg 1  if and only if

the flux superpotential is a small negative constant

    \[W_{{\rm{Flux}}}^{GV}\left( {\chi _\alpha ^ * ,{\tau ^ * }} \right) \equiv {W_0} \sim {10^{ - 4}}\]

and that to overcome the negative cosmological constant problem, our solutions can describe ‘the universe’

    \[{V_F} = - \frac{3}{{M_{pl}^2}}{\left| W \right|^2}{e^{{\rm K}/M_{pl}^2}}\]

via KKLT-uplifting of the AdS minima to positive energies by adding anti-D3-branes

which adds the Witten-term to the moduli potential

    \[{V_D} = \frac{D}{{{{\left( {\rho + \bar \rho } \right)}^2}}}\]

with D a constant that is a function of the D3-brane tension and the warping of the background,

thus gives us a realistic physical description at the cosmological level via the potential

    \[\begin{array}{c}V(\sigma ) = \frac{{aA}}{{2M_{pl}^2}}\frac{{{e^{ - a\sigma }}}}{{{\sigma ^2}}}\left( {\frac{1}{3}} \right.a\sigma A{e^{ - a\sigma }}\\{W_0} + \left. {A{e^{ - a\sigma }}} \right) + \frac{1}{4}\frac{D}{{{\sigma ^2}}}\end{array}\]

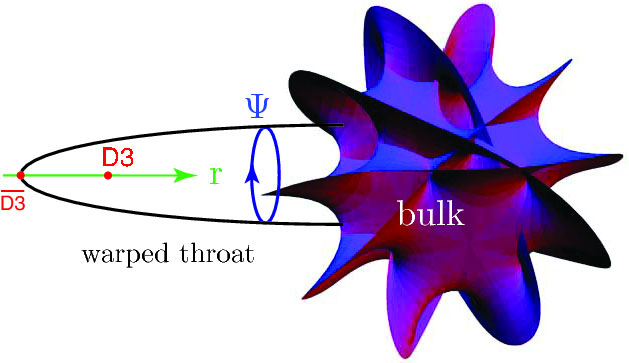
Now, a Klebanov-Strassler geometry naturally arises by considering string theory compactification on Ad{S_5} \times {X_5} where {X_5} is the Einstein manifold in five dimensions, with the interaction-Lagrangian of the massless Klebanov-Strassler field and the brane fields fermions is

    \[\begin{array}{*{20}{c}}{{\mathcal{L}^{KS}}_{\psi \bar \psi {H^0}}\frac{1}{{{M^{3/2}}}}\bar \psi \left[ {i{\gamma ^\mu }} \right.{\sigma ^{\mu \nu }}H_{\mu \nu \lambda }^0\left( {{x^\mu }} \right)}\\{\left. {\frac{{{\chi ^0}(r)}}{{\sqrt {\tau c} }}} \right]\psi }\end{array}\]

which, after integrating over the extra dimensional part, the effective 4-D Lagrangian reduces to

    \[\begin{array}{*{20}{c}}{\mathcal{L}_{\psi \bar \psi {H^0}}^{KS} = i\bar \psi {\gamma ^\mu }{\sigma ^{\mu \nu }}\left[ {\frac{{{e^{ - 4\pi K/{3_{{g_s}}}M}}}}{{{M_{pl}}}}} \right. \cdot }\\{\left. {\left( {\frac{{{r_{\max }}}}{{{r_0}}}} \right)} \right]H_{\mu \nu \lambda }^0\psi }\end{array}\]

with the fundamental Planck scale M and the 4-D Planck scale {M_{pl}} related as

    \[{M_{pl}} = \frac{{{M^{3/2}}}}{{\sqrt {2R} }}{r_{\max }}{\left( {1 - \frac{{r_0^2}}{{r_{\max }^2}}} \right)^{1/2}}\]

Now, the moduli spaces of compact Calabi-Yau spaces naturally contain conifold singularities. The local description of these singularities is called the conifold, a noncompact Calabi-Yau three-fold whose geometry is given by a cone and the orbifolded conifold equation

    \[\left\{ {\begin{array}{*{20}{c}}{C_{kl}^\wp :xy = {z^l}}\\{uv = {z^k}}\end{array}} \right.\]

allows us to consider the orbifolded conifold as a {C^ * } \times {C^ * } fibration over the z plane and is a chiral theory with the gauge group

    \[\prod\limits_{i,j}^2 {SU{{(M)}_{i,j}}} \times \prod\limits_{i,j}^2 {SU{{(M)'}_{i,j}}} \]

and because the T-dual theory contains NS branes which are perpendicular, the adjoint fields become massive and they are integrated out, leaving only quadratic terms in the superpotential. The singular conifold is defined by the complex equation

    \[\left\{ {\begin{array}{*{20}{c}}{\sum\limits_{i = 1}^4 {z_i^2 = 0} }\\{{z_i} \in \mathbb{C}}\end{array}} \right.\]

and the Calabi-Yau metric on the conifold is

    \[ds_6^2 = d{r^2} + {r^2}ds_{{T^{1,1}}}^2\]

with the radial coordinate \tau definable via

    \[r \equiv {\sum\nolimits_{i = 1}^4 {\left| {{z_i}} \right|} ^2}\]

and the base of the cone is the {T^{1,1}} coset space

    \[\left[ {SU{{(2)}_A} \times SU{{(2)}_B}} \right]/U{(1)_K}\]

with the topology {S^2} \times {S^3} and the metric of {T^{1,1}} in angular coordinates {\theta _i} \in \left[ {0,\pi } \right], {\phi _i} \in \left[ {0,2\pi } \right], \psi \in \left[ {0,4\pi } \right] is

    \[\begin{array}{c}ds_{{T^{1,1}}}^2 = \frac{1}{6}\left( {d\psi + \sum\limits_{i = 1}^2 {\cos {\theta _i}d{\phi _i}} } \right) + \\\frac{1}{6}\sum\limits_{i = 1}^2 {\left( {d\phi _i^2 + {{\sin }^2}{\theta _i}d\phi _i^2} \right)} \end{array}\]

Hence, the space defined by

    \[\left\{ {\begin{array}{*{20}{c}}{\sum\limits_{i = 1}^4 {z_i^2 = 0} }\\{{z_i} \in \mathbb{C}}\end{array}} \right.\]

is singular at the tip of the cone r = 0. One can remove this singularity via a deformed conifold defined by

    \[\sum\limits_{i = 1}^4 {z_i^2} = {\varepsilon ^2}\]

with \varepsilon \in \mathbb{C} and by a phase rotation of the {z_i} coordinates, we can always choose \varepsilon \in {\mathbb{R}^ + } which defines a one-dimensional moduli space. For large r the deformed conifold geometry reduces to the singular conifold with \varepsilon = 0. Moving from large r towards the origin, the sizes of the {S^2} and {S^3} both decrease. Decomposing the {z_i} into real and imaginary parts one finds

    \[\left\{ {\begin{array}{*{20}{c}}{{\varepsilon ^2} = \vec x \cdot \vec x - \vec y \cdot \vec y}\\{{\rho ^2} = \vec x \cdot \vec x - \vec y \cdot \vec y}\end{array}} \right.\]

which shows that the range of \rho or r is limited by

    \[{\varepsilon ^2} \le {\rho ^2} < \infty \]

thus the singularity at r = 0 is avoided since we now have {\varepsilon ^2} > 0.

Now, a stack of N D3-branes placed at the singularity {z_i} = 0 backreacts on the geometry, creating a warped background with the following ten dimensional line element

    \[\begin{array}{c}d{s^2} = {h^{1/2}}(z){g_{\mu \nu }}d{x^\mu }d{x^\nu } + \\{h^{ - 1/2}}(z){g_{i\overline j }}d{z^i}d{z^{\overline j }}\end{array}\]

with {g_{i\overline j }} the metric

    \[\begin{array}{c}ds_{{T^{1,1}}}^2 = \frac{1}{6}\left( {d\psi + \sum\limits_{i = 1}^2 {\cos {\theta _i}d{\phi _i}} } \right) + \\\frac{1}{6}\sum\limits_{i = 1}^2 {\left( {d\phi _i^2 + {{\sin }^2}{\theta _i}d\phi _i^2} \right)} \end{array}\]

and the warp factor is

    \[\left\{ {\begin{array}{*{20}{c}}{h(r) = \frac{{{R^4}}}{{{r^4}}}}\\{{R^4} \equiv \frac{{2z\pi }}{4}{g_s}N{{(\alpha ')}^2}}\end{array}} \right.\]

and

the deep part is that this AdS background is an explicit realization of the Randall-Sundrum scenario in string theory

that I discussed here and here. So in line with the AdS/CFT duality, the Ad{S_5} \times {T^{1,1}} geometry

has a dual gauge theory interpretation

namely, an SU(N) \times SU(N) gauge theory coupled to bifundamental chiral superfields, and adding M D5-branes wrapped over the {S^2} inside {T^{1,1}}, then the gauge group becomes

    \[SU\left( {N + M} \right){\rm{ }} \times {\rm{ }}SU\left( N \right)\]

giving a cascading gauge theory. The three-form flux induced by the wrapped D5-branes – fractional D3-branes – satisfies

    \[\frac{1}{{{{\left( {2\pi } \right)}^2}\alpha '}}\int_{{S^3}} {{F_3}} = M\]

and the Klebanov-Strassler warp-throat factor is

    \[\begin{array}{c}h(r) = \frac{{27\pi {{\left( {\alpha '} \right)}^2}}}{{4{r^2}}}\left[ {{g_s}} \right.N + \frac{2}{{2\pi }}\\{\left( {{g_s}M} \right)^2}{\rm{In}}\left( {\frac{r}{{{r_0}}}} \right) + \frac{3}{{8\pi }}\left. {{{\left( {{g_s}M} \right)}^2}} \right]\end{array}\]

with

    \[{r_0} \sim {\varepsilon ^{2/3}}{e^{2\pi N/\left( {3{g_s}M} \right)}}\]

and that Klebanov-Strassler warp-throat conifold background will be the basis for our explicit analysis of warped D-brane inflationary cosmology 

previously

M-Theory, BraneWorld Cosmology, and Calabi-Yau Compactification

up next

5-D AdS/CFT Warped-Throat Calabi-Yau N-fold Analysis and Klebanov-Strassler Theory
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on