Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

Klebanov-Strassler Warped Conifold Analysis, Calabi-Yau 3-Fold and AdS/CFT Duality

By Posted on In Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Philosophy Of Physics, Physics, Super String Theory, Supersymmetry ,
photo

I last showed that the AdS/CFT correspondence states that, for large N, classical supergravity on this background is dual to strongly coupled 4-d N = 4 SU(N) superYang-Mills theory and the conformality of the 4-d theory is reflected by translational invariance along the r direction of the 5-d AdS space and provides a stringy realization of the Randall-Sundrum-II model

This is deep, and in this post, I will delve into Klebanov-Strassler warped throat conifold analysis. Recal that the low-energy limit of type IIB superstring theory is type IIB supergravity, whose action is

    \[\begin{array}{c}S = \frac{{M_{10}^8}}{2}\int {{d^{10}}} x\sqrt { - g} \left( {R - \frac{{{{\left| {{{\not \partial }_\tau }} \right|}^2}}}{{2{{\left( {{\rm{Im}}\tau } \right)}^2}}}} \right.\\ - \frac{{{{\left| {{G_3}} \right|}^2}}}{{12{\rm{Im}}\tau }} - \left. {\widetilde F_5^2} \right) + \\\frac{{M_{10}^8}}{{8i}}\int {\frac{{{C_4} \wedge {G_3} \wedge {{\bar G}_3}}}{{{\rm{Im}}\tau }}} + fermions\end{array}\]

by which is meant ‘fermion-terms’, with {M_{10}} the 10-d reduced Planck mass, and g the 10-d Einstein frame metric with Ricci scalar R, and \tau is the axio-dilaton, formed from the Ramond-Ramond axion {C_0}, with the dilaton \phi defined by

    \[\tau = {C_0} + i{e^{ - \phi }}\]

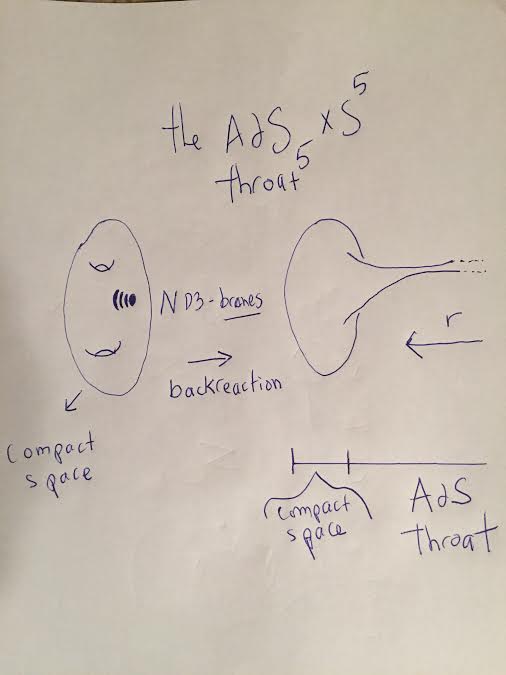
and that placing N coincident D3-branes in 10-d flat spacetime will deform the warped-throat internal-space metric, thus yielding

    \[\begin{array}{c}d{s^2} = H{(r)^{ - 1/2}}{\eta _{\mu \nu }}d{x^\mu }d{x^\nu } + \\h{(r)^{1/2}}\left( {d{r^2} + {r^2}ds_{{S^5}}^2} \right)\end{array}\]

with

    \[\left\{ {\begin{array}{*{20}{c}}{h(r) = 1\frac{{{R^4}}}{{{r^4}}}}\\{{R^4} = 4\pi {g_s}N{{\alpha '}^2}\frac{{{\pi ^3}}}{{{\rm{Vol}}\left( {{S^5}} \right)}} = 4\pi {g_s}N{{\alpha '}^2}}\end{array}} \right.\]

visually…

photo

and this space is asymptotically flat as r \to \infty, given that h(r) \to 1. For small r, the second term dominates, and the metric becomes that of Ad{S_5} \times {S^5}

    \[\begin{array}{c}d{s^2} = \frac{{{r^2}}}{{{R^2}}}{\eta _{\mu \nu }}d{x^\mu }d{x^\nu } + \\\frac{{{R^2}}}{{{r^2}}}d{r^2} + {R^2}ds_{{S^5}}^2\end{array}\]

with the branes sourcing N units of {\widetilde F_5} flux through the internal  {S^5}. In this post, I will try and show via

Klebanov-Strassler warped conifold analysis, that the AdS/CFT dual of supergravity on the warped conifold background is a 4-D N = 1 superconformal gauge theory

First, note that a Klebanov-Strassler geometry naturally arises by considering string theory compactification on Ad{S_5} \times {X_5} where {X_5} is the Einstein manifold in five dimensions, with the interaction-Lagrangian of the massless Klebanov-Strassler field and the brane fields fermions is

    \[\begin{array}{c}{{\not L}^{KS}}_{\psi \bar \psi {H^0}}\frac{1}{{{M^{3/2}}}}\bar \psi \left[ {i{\gamma ^\mu }} \right.{\sigma ^{\mu \nu }}H_{\mu \nu \lambda }^0\left( {{x^\mu }} \right)\\\left. {\frac{{{\chi ^0}(r)}}{{\sqrt {\tau c} }}} \right]\psi \end{array}\]

and after integrating over the extra dimensional part, the effective 4-D Lagrangian reduces to

    \[\begin{array}{c}\not L_{\psi \bar \psi {H^0}}^{KS} = i\bar \psi {\gamma ^\mu }{\sigma ^{\mu \nu }}\left[ {\frac{{{e^{ - 4\pi K/{3_{{g_s}}}M}}}}{{{M_{pl}}}}} \right. \cdot \\\left. {\left( {\frac{{{r_{\max }}}}{{{r_0}}}} \right)} \right]H_{\mu \nu \lambda }^0\psi \end{array}\]

with the fundamental Planck scale M and the 4-D Planck scale {M_{pl}} related as

    \[{M_{pl}} = \frac{{{M^{3/2}}}}{{\sqrt {2R} }}{r_{\max }}{\left( {1 - \frac{{r_0^2}}{{r_{\max }^2}}} \right)^{1/2}}\]

Let us consider a IIB compactification on a Calabi-Yau 3-fold M which has a conical singularity. Placing N D3-branes at the singular point yields a deformation of the metric as in above, and is

    \[\begin{array}{c}d{s^2} = h{(r)^{ - 1/2}}{\eta _{\mu \nu }}d{x^\mu }d{x^\nu } + \\h{(r)^{1/2}}\left( {d{r^2} + {r^2}ds_{{X_5}}^2} \right)\end{array}\]

with

    \[\left\{ {\begin{array}{*{20}{c}}{h(r) = 1 + \frac{{{R^2}}}{{{r^4}}}}\\{{R^4} = 4\pi {g_s}N{{\alpha '}^2}\frac{{{\pi ^3}}}{{{\rm{Vol}}\left( {{X_5}} \right)}}}\end{array}} \right.\]

And this is deep because:

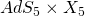spacetime at small r converges to the Ad{S_5} \times {X_5} throat, whereas at large r it is given by {\mathbb{R}^{3,1}} \times {C_{{X_5}}}

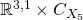
and hence, in the throat, supergravity is dual to a conformal field theory in 4-D. The Klebanov-Strassler warped deformed conifold arises by considering

    \[{X_5} = {T^{1,1}} = \left( {SU(2) \times SU(2)} \right)/U(1)\]

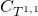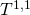The conifold is the cone {C_{{T^{1,1}}}} over {T^{1,1}}: a non-compact singular Ricci-flat manifold

The metric near N D3-branes at a conifold singularity is

    \[\begin{array}{c}d{s^2} = h{(r)^{ - 1/2}}{\eta _{\mu \nu }}d{x^\mu }d{x^\nu } + \\h{(r)^{1/2}}\left( {d{r^2} + {r^2}ds_{{T^{1,1}}}^2} \right)\end{array}\]

and with

    \[\left\{ {\begin{array}{*{20}{c}}{h(r) = 1 + \frac{{{R^4}}}{{{r^4}}}}\\{{R^4} = \frac{{27\pi }}{4}{g_s}N{{\alpha '}^2}}\end{array}} \right.\]

with solution N units of {\widetilde F_5} flux through the internal {T^{1,1}}, visually as

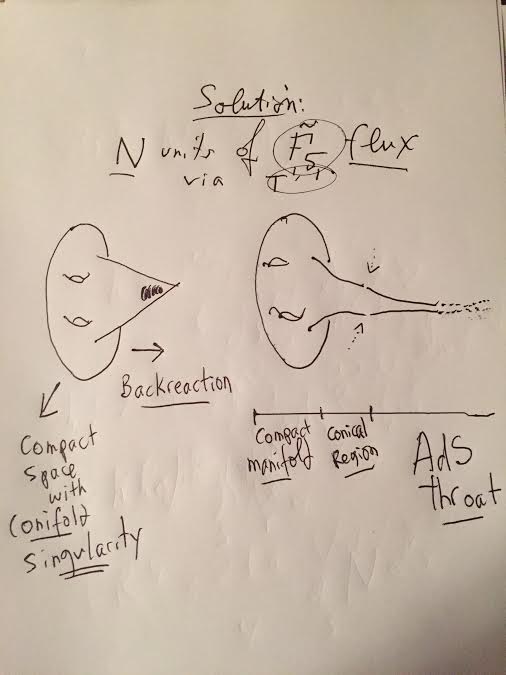
photo

and {T^{1,1}} is topologically {S^3} \times {S^2},

and at the conifold singularity both the 3-cycle and the 2-cycle shrink to zero size

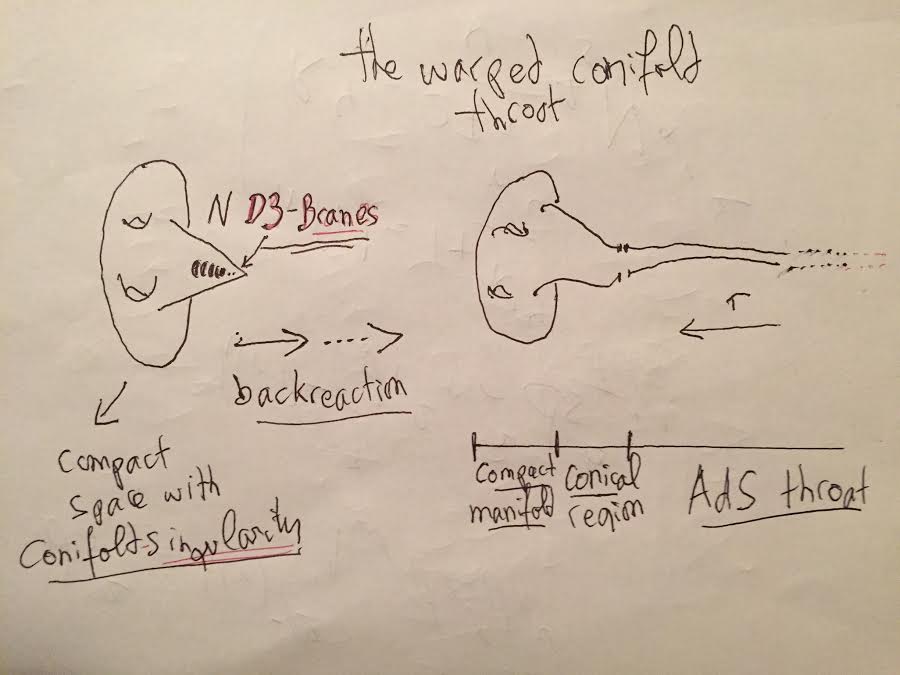
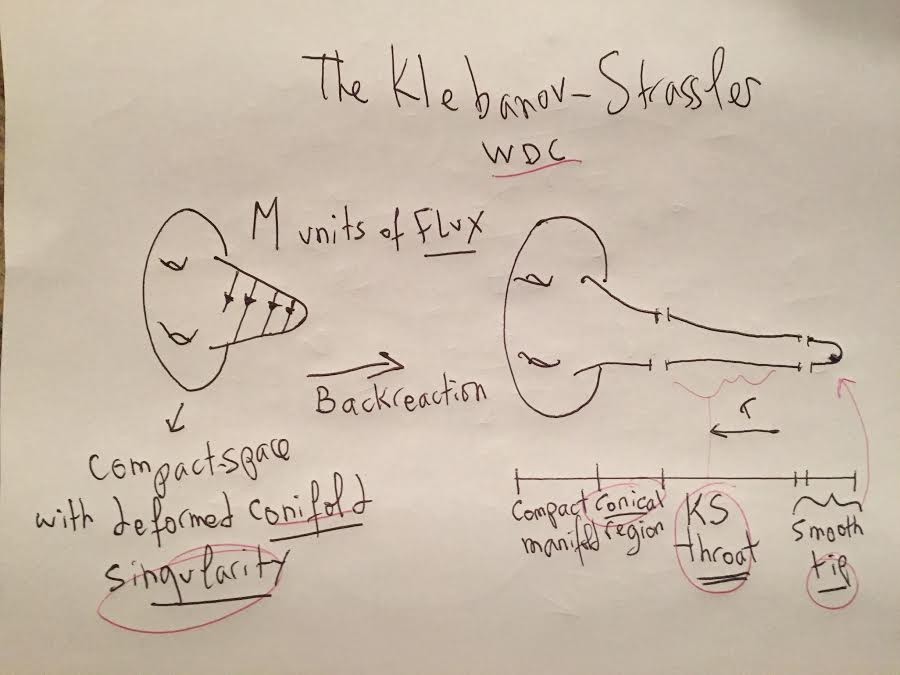
The deformed conifold is a non-singular, non-compact manifold that admits a Calabi-Yau metric and when placing M units of {F_3} flux on the 3-cycle, the flux backreaction on the geometry gives the warped deformed conifold. One can interpret this {F_3} flux as sourced by D-branes and crucially, as noted visually, in the warped conifold throat context, D3-branes live at the singularity

photo

The throat metric, excluding the tip, is the Klebanov-Tseytlin one

    \[\begin{array}{c}d{s^2} = \tilde h{(r)^{ - 1/2}}{\eta _{\mu \nu }}d{x^2}d{x^\nu } + \\\tilde h{(r)^{1/2}}\left( {d{r^2} + {r^2}ds_{{T^{1,1}}}^2} \right)\end{array}\]

with

    \[\left\{ {\begin{array}{*{20}{c}}{\tilde h(r) = 1 + \frac{{R_{eff}^4(r)}}{{{r^4}}}}\\{R_{eff}^4(r) = \frac{{27}}{4}\pi {g_s}(r){{\alpha '}^2}}\\{{N_{eff}}(r) = \frac{3}{{2\pi }}{g_s}{M^2}\log \frac{r}{{{r_s}}}}\end{array}} \right.\]

with {r_s} is the singularity deformation parameter size, and the Klebanov-Tseytlin metric becomes singular for r \to {r_s} and no longer valid in the domain r{ \ll _ \sim }{r_s}, and the complete throat is perfectly smooth also at its tip, thus we have the following ‘picture’

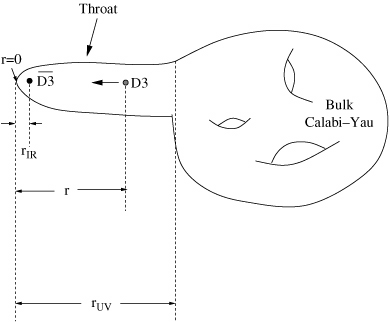
photo

And as one goes along the throat, there are {N_{eff}}(r) units of {\tilde F_5} flux through {T^{1,1}} at the radial coordinate r

    \[\begin{array}{c}\left( {4{\pi ^2}\alpha '} \right){N_{eff}}(r) = \int\limits_{{T^{1,1}}\,{\rm{at}}\,r} {{{\tilde F}^5}} = \\\left( {\int\limits_{{S^3}\,{\rm{at}}\,r} {{F_3}} } \right)\left( {\int\limits_{{S^2}\,{\rm{at}}\,r} {{B_2}} } \right)\end{array}\]

With the general ansatz

    \[\begin{array}{c}d{s^2} = \tilde h{(r)^{ - 1/2}}{\eta _{\mu \nu }}d{x^2}d{x^\nu } + \\\tilde h{(r)^{1/2}}\left( {d{r^2} + {r^2}ds_{{T^{1,1}}}^2} \right)\end{array}\]

the logarithmic dependence

    \[\left\{ {\begin{array}{*{20}{c}}{\tilde h(r) = 1 + \frac{{R_{eff}^4(r)}}{{{r^4}}}}\\{R_{eff}^4(r) = \frac{{27}}{4}\pi {g_s}(r){{\alpha '}^2}}\\{{N_{eff}}(r) = \frac{3}{{2\pi }}{g_s}{M^2}\log \frac{r}{{{r_s}}}}\end{array}} \right.\]

of {N_{eff}}  on r can be be gotten as such: for a finite segment of the throat, between {r_1} and {r_2}, we have

    \[\begin{array}{c}{\left( {4{\pi ^2}\alpha '} \right)^2}\left( {{N_{eff}}({r_2}) - {N_{eff}}({r_1})} \right) = \\\int\limits_{{T^{1,1}}\,{\rm{at}}\,{r_2}} {{{\tilde F}_5}} - \int\limits_{{T^{1,1}}\,{\rm{at}}\,{r_1}} {{{\tilde F}_5}} = \\\int\limits_{{T^{1,1}} \times \left[ {{r_1};{r_2}} \right]} {d{{\tilde F}_5}} = \int\limits_{{T^{1,1}} \times \left[ {{r_1};{r_2}} \right]} {{H_3} \wedge {F_3}} \end{array}\]

Since {G_3} is imaginary self-dual, one has

    \[{H_3} = {g_s} * _{6D}^{{\rm{Hodge - Star}}}{F_3}\]

and because {F_3} has zero components in the r direction, one can derive

    \[\begin{array}{c}{H_3} \wedge {F_3} = {g_s}\sqrt {{g_6}} {F_{mnp}}{F^{mnp}}{d^6}y = \\\frac{{{g_s}}}{r}\sqrt {\bar g} {F_{\bar m\bar n\bar p}}{F^{\bar m\bar n\bar p}}dr{d^5}\bar y\end{array}\]

with the {T^{1,1}} metric being

    \[{\bar g_{\bar m\bar n}}d\,{\bar y^{\bar m}}d\,{\bar y^{\bar n}} = d_{{T^{1,1}}}^2\]

and inserting into

    \[\begin{array}{c}{\left( {4{\pi ^2}\alpha '} \right)^2}\left( {{N_{eff}}({r_2}) - {N_{eff}}({r_1})} \right) = \\\int\limits_{{T^{1,1}}\,{\rm{at}}\,{r_2}} {{{\tilde F}_5}} - \int\limits_{{T^{1,1}}\,{\rm{at}}\,{r_1}} {{{\tilde F}_5}} = \\\int\limits_{{T^{1,1}} \times \left[ {{r_1};{r_2}} \right]} {d{{\tilde F}_5}} = \int\limits_{{T^{1,1}} \times \left[ {{r_1};{r_2}} \right]} {{H_3} \wedge {F_3}} \end{array}\]

and differentiating, one gets

    \[\begin{array}{c}\frac{{d{N_{eff}}(r)}}{{dr}} = \frac{{{g_s}}}{{{{\left( {4{\pi ^2}\alpha '} \right)}^2}}} \cdot \\\int\limits_{{T^{1,1}}} {{d^5}} \bar y\sqrt {\bar g} {F_{\bar m\bar n\bar p}}{F^{\bar m\bar n\bar p}}\end{array}\]

and with the quantization condition

    \[\frac{1}{{4{\pi ^2}\alpha '}}\int_{{S^3}} {{F_3}} = M\]

implying the scaling {F_3} \sim M\alpha ' for the non-vanishing components of {F_3}, we get our desired result

    \[{N_{eff}}(r) = a{g_s}{M^2}\log \left( {r/{r_s}} \right)\]

And the intended goal: the AdS/CFT dual of supergravity on the KS warped conifold background is a 4-D N = 1 superconformal gauge theory and the internal compactification-topology and flux-quanta have backgrounds essentially containing KS warped throats

previously

5-D AdS/CFT Warped-Throat Calabi-Yau N-fold Analysis and Klebanov-Strassler Theory

up next

Randall-Sundrum Geometry and the Klebanov-Strassler Throat
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on