All quantum-gravity theories, most famously being String/M-theory and Loop Quantum Gravity, exhibit Lorentz invariance violation: here is why; thus posing an apriori problem in attempting a quantization of gravity: canonical or not. As I will show here, establishing an analytic-emergence relation between SU(N)-Gauge-Theory and the non-Abelian Nambu-Goldstone model (NANGM) restores L-symmetry at all Hopf-rooted-tree levels of the renormalization group algebra.
P. Aschieri’s Noncommutative Differential Geometry: Quantization of Connections and Gravity is an excellent read and a great backdrop to this post. Let me describe the non-Abelian Nambu-Goldstone model via the Lagrangian density:
![]()
and the action-variation relative to ![]() ,
, ![]() gives us the EoMs:
gives us the EoMs:
![]()
with the following relations holding:
![]()
where the NANGM-action is given by:
![]()
and:
![]()
with conditions
![]()
![]()
an oriented constant vector,
![]()
the Lorentz spontaneous symmetry breaking term,
![]()
the Lorentz and gauge group indices with ![]() -generators.
-generators.
It follows from
![]()
that there exists a nonzero vacuum expectation value:
![]()
guaranteeing the spontaneous symmetry breaking of Lorentz invariance and the existence of Goldstone bosons, which follows from Goldstone’s theorem. One then parametrizes the Non-Abelian Nambu-Goldstone Model via
![]()
with:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{N = \left( {A_{\bar \iota }^bA_{\bar \iota }^b + {n^2}{M^2}} \right)}\\{4{B^2} \pm N \ne 0}\\{\bar \iota = 1,2}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c9856243e2a7d6981574144d650a0fba_l3.png)
After substituting
![]()
in the Lagrangian density:
![]()
we get the variation of the action relative to ![]() ,
, ![]() , yielding the equation of motion:
, yielding the equation of motion:
![]()
with:
and
![]()
In the context of the SO(N) Yang Mills theory the equations of motion are 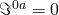
thus, we do not have current conservation:
![]()
due to the fact that the conditions:
![]()
are not gauge-invariant. However, by imposing the Gaussian condition:
![]()
we recover gauge-invariance of the Yang Mills equations of motion. With invertible coordinate transformation:
![]()
its crucial transformation properties are:
![]()
and
![]()
Let me proceed to the Hamiltonian aspect of the analytic-emergence relation between SU(N)-Gauge-Theory and the non-Abelian Nambu-Goldstone model
Getting the exact Hamiltonian, let its density be expressed in terms of the conjugated variables ![]() ,
, ![]() . Hence, given:
. Hence, given:
![]()
and the substitution in the Lagrangian density above, one can split:
![]()
as such:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{L^{NG}}_{na}\left( {\Phi ,\dot \Phi } \right) = \frac{1}{2}E_i^aE_i^a - \\\frac{1}{2}B_i^aB_i^a - {J^{a\mu }}A_\mu ^a\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-fc75aeeb23e09677cc33047108193565_l3.png)
with
![]()
thus, we get the canonically conjugated momenta:
![Rendered by QuickLaTeX.com \[\prod _A^a = \frac{{\not \partial {L^{NG}}_{na}\left( {\Phi ,\dot \Phi } \right)}}{{\not \partial \dot \Phi _A^a}} = E_i^b\frac{{\not \partial \dot A_i^b}}{{\not \partial \dot \Phi _A^a}} = E_i^b\frac{{\not \partial A_i^b}}{{\not \partial \Phi _A^a}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1f752c886fb33b7a864475639d9cc1f9_l3.png)
The inverse of
![]()
allows us to express ![]() as a function of the momenta
as a function of the momenta ![]() of the Non-Abelian Nambu-Goldstone Model in the following form:
of the Non-Abelian Nambu-Goldstone Model in the following form:
![]()
Hence, and this is deep, the Wronskian of the system is
Which is gauge-invariant and exhibits parametric renormalization-group finiteness
Therefore, the Non-Abelian Nambu-Goldstone Model Hamiltonian density is:
![]()
successively expressed as:
![]()
hence the dependence upon the canonical variables ![]() ,
, ![]() can be gotten via change of variables w.r.t.
can be gotten via change of variables w.r.t.
![]()
![]()
so the canonical variables satisfy the Poisson bracket algebra
![]()
and
![Rendered by QuickLaTeX.com \[\left\{ {\prod _A^a\left( x \right),\prod _B^b\left( y \right)} \right\} = 0\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-16c75d99f1f7271b296b24a07f4c3d2a_l3.png)
and
![Rendered by QuickLaTeX.com \[\left\{ {A_A^a\left( x \right),\prod _B^b\left( y \right)} \right\} = {\delta ^{ab}}{\delta _{AB}}{\delta ^3}\left( {x - y} \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-0f0420c3ff181ffa087aa7dcf112fcfd_l3.png)
allowing us to derive the theory’s Hamiltonian action:
![]()
with
![]()
the canonically conjugated momenta of ![]() , and so,
, and so,
![]()
hence, given:
![]()
we get:
![Rendered by QuickLaTeX.com \[A_0^a = \frac{{A_3^a}}{{\sqrt {A_3^bA_3^b} }}\left( {\sqrt {A_i^bA_i^b + {n^2}{M^2}} } \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c64aa60b7f377c1a1045315fa3d895ac_l3.png)
and since the transformations
![]()
are generated from change-of-variables,
![]()
in coordinate space,
it follows from quantum-mechanics that the full transformation in the phase space is canonical. Thus, we can recover the Poisson bracket algebra
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\left\{ {A_i^a\left( x \right),A_j^b\left( y \right)} \right\} = 0}\\{\left\{ {{E^{ai}}\left( x \right),{E^{bj}}\left( y \right)} \right\} = 0}\\{\left\{ {A_i^a\left( x \right),{E^{bj}}\left( y \right)} \right\} = - {\delta ^{ab}}\delta _i^j{\delta ^3}\left( {x - y} \right)}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c7741252cd3535b3d7ea5d88ac13c812_l3.png)
So, the time-evolution of the Gaussian functions under the dynamics of the NANGM is given by:
with ![]() determined by:
determined by:
![]()
When one imposes the Gaussian constraints as initial conditions:
![]()
the standard Yang-Mills equations of motion are validly recovered at ![]() , and given the antisymmetry of Maxwellian tensor, we get:
, and given the antisymmetry of Maxwellian tensor, we get:
![]()
at ![]() , and given
, and given
![]()
one gets:
![]()
solving, we get:
![]()
Therefore, the Yang Mills equations are now valid at ![]() , entailing, by Maxwellian conditions, current conservation also at
, entailing, by Maxwellian conditions, current conservation also at ![]() .
.
So, we recover the SU(N) Yang-Mills theory by imposing the Gaussian laws as Hamiltonian metaplectic constraints, with functions ![]() adding
adding ![]() to
to ![]() , thus getting a redefinition:
, thus getting a redefinition:
![]()
This leads to:
![]()
establishing, upon dimensional generalization, not only an emergent-relation between SU(N)-Gauge-Theory and Non-Abelian Nambu-Goldstone Model, but a stronger thesis:

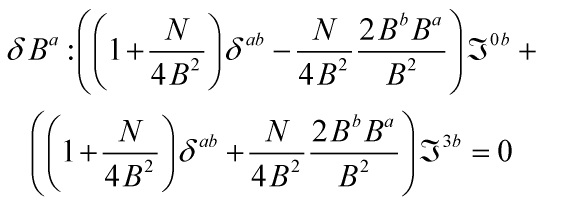
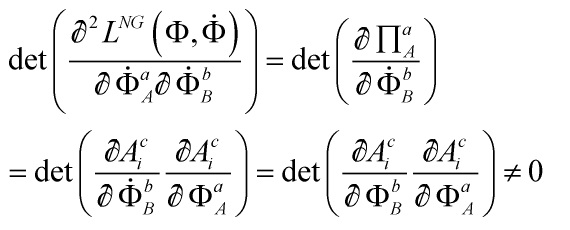
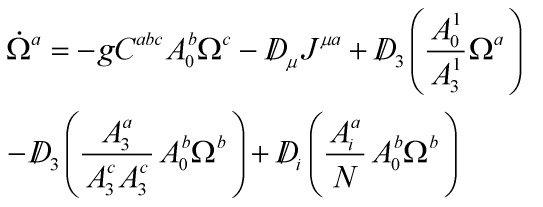



1 Response
Quantum Geometry, Emergence and Noncommutative Spacetime
Friday, August 5, 2016[…] as emergent properties of symplectic noncommutative spacetime. Again, two good references are my last post and P. […]