D3-Brane Self-Duality And Super-Hamiltonian Action Under Poincaré Invariance

By George Shiber Sunday, May 31, 2015Friday, October 26, 2018 In Grand Unification Physics, M Theory, Mathematical Physics, Philosophy Of Mathematics, Philosophy Of Physics, Philosophy Of Science, Super String Theory, Supersymmetry Atiyah-Singer Index Theorem, automorphic group

Well, a big question is how did the universe begin. And we, cannot answer that question. Some people think that the big bang is an explanation of how the universe began, IT IS NOT. The big bang is a theory of how the universe evolved from a split second after whatever brought it into existence. And the reason why we’ve been unable to look right back at time zero, to figure out how it really began; is that conflict between Einstein’s ideas of gravity and the laws of quantum physics. So, STRING THEORY may and will be able to – it hasn’t yet; we’re working on it today – feverishly. It may be able to answer the question, how did the universe begin. And I don’t know how it’ll affect your everyday life, but to me, if we really had a sense of how the universe really began, I think that would, really, alert us to our place in the cosmos in a DEEP way. ~ Brian Greene!

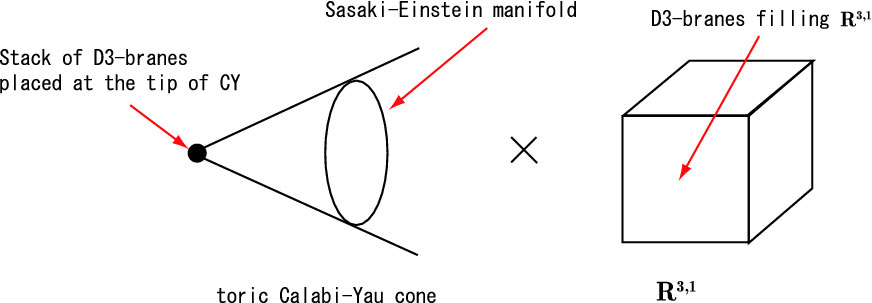
I listed the 4 essential properties of D3-branes, namely: i) the propagation of a D3-brane through spacetime generates a 4-dimensional worldvolume that has 4-dimensional Poincaré invariance, ii) the string worldsheet generating the graviton via quantum fluctuation can be topologically compactified on the boundary of its corresponding $Ad{S_4} \times {S^4}$ space, iii) D3-branes have constant axion and dilaton fields, and for the purposes of this post, iv) D3-branes are self-dual. Thus, the gravitonic D3-brane action with a super-Lagrangian coupling can be derived as

${S_{D3}} = \frac{1}{{4{k^2}{C_{\left[ 4 \right]}}}}\int {\sqrt {\widetilde {{k_{\mu \nu }}^{ - 2\Phi }}} } \left( {2{k^{\mu \nu }}{C_{\left[ 2 \right]}} + \frac{\lambda }{8} + {{\not \partial }_\mu }\Phi \,\partial _\phi ^\mu \Phi - C_{\left[ 4 \right]}^\Phi - 1{K_{\mu \nu }}^{ * \dagger }} \right){L_{G(D3)}}$

with

${L_{G(D3)}} \equiv \widetilde {{L_G}}\left( {{F_{\mu \nu }},{\chi ^a},\theta ;\,\phi ,\chi } \right) = {L_G}\left( {{e^{ - \Phi /2}}{F_{\mu \nu }},{\chi ^a},\theta } \right) - \frac{1}{4}{\chi ^a}{F_{\mu \nu }}{\widetilde F_{\mu \nu }}$

However, as I showed, one must exhibit the self-duality of the D3-brane in the Hamiltonian setting. It is my aim in this post to provide the proof. One can always lift an $SO(2)$ duality to an $S(2,\Re )$ duality by introducing the D3-brane dilaton $\phi$ and axion $\chi$ which are constant background fields. Then, one can re-define an $SO(2)$ duality Lagrangian as such:

$\widetilde L\left( {F,X,\theta ;\phi ,\chi } \right) = {L_G}\left( {{e^{ - \Phi /2}}F,X,\theta } \right) - \frac{1}{4}\chi F\,\widetilde F$

with $\widetilde F = {e^{ - \Phi /2}}F$ . From the above $SO(2)$ dual Lagrangian, the D3-brane Hamiltonian action can be derived as

$S = \int {{d^4}} \sigma {L^{DBI}} + \int {{L^{WZ}}} - \int {\frac{1}{2}} \,\chi {F^2} = \int {{d^4}} \sigma L_G^{{\rm{Total}}}$

where

$\left\{ {\begin{array}{*{20}{c}}{{L^{DBI}} = - \sqrt { - {\rm{det}}\left( {{G_{\mu \nu }} + {F_{\mu \nu }}} \right)} }\\{{G_{\mu \nu }} = \prod _\mu ^M{\prod _\mu }M}\\{{F_{\mu \nu }} = {{\not \partial }_{\left[ {\mu A\nu } \right]}} + \Omega _{\mu \nu }^3}\\{\Omega _{\mu \nu }^i = {{\widetilde {\theta {{\not \prod }_{{{\left[ {\mu {\tau _j}{{\not \partial }_\nu }} \right]}^\theta }}}}}^{ * \dagger }}}\end{array}} \right.$

$(j = 1,3)$ and ${\tau _i}$ are the Pauli matrices cohomologically acting on the supersymmetric group indices, and ${L^{WZ}}$ is the Wess-Zumino Lagrangian satisfying the Matsubara condition, and is given by

$\left\{ {\begin{array}{*{20}{c}}{{L^{WZ}} = {C^{(2)}}{F_{\mu \nu }} + C(4)}\\{{C^{(2)}} = \widetilde \theta {{\not \prod }^{ * \dagger }}{\tau _i}\,d\theta = {\Omega _1}}\\{{C^{(4)}} = \Xi \,\; - \frac{1}{2}{\Omega _1}\,{\Omega _3}}\end{array}} \right.$

where ${C^{(2)}}$ and ${C^{(4)}}$ are RR-2 and RR-4 differential forms, and $\Xi$ represents the Kappa symmetry of the gauge bundle of the D3-brane’s $Ad{S_4} \times {S^4}$ topology. Now, let

$\left\{ {\begin{array}{*{20}{c}}{\left( {{X^M},{P^M}} \right)}\\{\left( {\theta ,\,{\pi _\theta }} \right)}\\{\left( {{A_\mu },{E^\mu }} \right)}\end{array}} \right.$

be a canonical conjugate set for the super-Kahler phase space variables, and define the critical 3-dimensional anti-symmetric tensor

${\varepsilon ^{ijk}} = {\varepsilon ^{0ijk}}$

and introduce the de Rham variables

$\left\{ {\begin{array}{*{20}{c}}{{{\not B}^i} = \frac{1}{2}{\varepsilon ^{ijk}}{F_{ik}} = {e^{ - \Phi /2}}{B^i} + \frac{1}{2}{\varepsilon ^{ijk}}\Omega _{jk}^3}\\{{B^i} = \frac{1}{2}{\varepsilon ^{ijk}}{F_{ij}}\;;\,\;\left( {i,j,k = 1,2,3} \right)}\\{{{\not P}_M} \equiv \frac{{\partial {L^{DBI}}}}{{\partial \prod _0^M}} = P_M^{ * \dagger } - {e^{\phi /2}}{{\left( {E + \chi B} \right)}^i} \cdot \frac{{\partial {F_{0i}}(\prod ,\widetilde \theta )}}{{\partial \prod _0^M}} - \frac{{\partial {L^{WZ}}\left( {\prod ,F,\widetilde \theta } \right)}}{{\partial \prod _0^M}}}\\{{{\not \Sigma }^i} \equiv \frac{{\partial {L^{DBI}}}}{{\partial {F_{0i}}}} = {e^{\phi /2}}{{\left( {E + \chi B} \right)}^i} - \frac{{\partial {L^{WZ}}\left( {\prod ,F,\widetilde \theta } \right)}}{{\partial {F_{0i}}}}}\end{array}} \right.$

where ${\not \Sigma ^i}$ transforms as

$\delta {\not \Sigma ^i} = \not \partial {L^{{\rm{Total}}}}/\not \partial {F_{0i}}$

One then finds that the constraints of the system to be given by

– $U(1)$ symmetry constraint

– ${\not \Sigma ^0} = 0$

– ${\partial _i}{\not \Sigma ^i} = 0$

and

– the p + 1 diffeomorphism constraints

$\left\{ {\begin{array}{*{20}{c}}{{\varphi _i} \equiv \not P \cdot {\prod _i} + {{\not \Sigma }^{ij}}{F_{ij}} = \not P \cdot {\prod _i} + \,{\varepsilon _{ijk}}\,{{\not \Sigma }^j}{{\not B}^k} = 0}\\{{\varphi _0} \equiv \frac{1}{2}\left[ {{{\not P}^2} + \gamma + {\gamma _{ij}}\left( {{{\not \Sigma }^i}{{\not \Sigma }^j} + {{\not B}^i}{{\not B}^j}} \right)} \right] = 0}\end{array}} \right.$

and

– the fermionic constraints

$\begin{array}{c}\psi \equiv {\pi _0} - {{\not P}_M}\frac{{\not \partial \prod _o^M}}{{\not \partial \widetilde \theta }} - {e^{\phi /2}}{\left( {E + \chi \not B} \right)^i}\frac{{\not \partial {F_{0i}}\left( {\prod ,\widetilde \theta } \right)}}{{\not \partial \widetilde \theta }}\\ - \frac{{\not \partial {L^{WZ}}\left( {\prod ,F,\widetilde \theta } \right)}}{{\not \partial \widetilde \theta }}\end{array}$

with ${\gamma _{ij}}$ being the spatial part of the $Ad{S_4} \times {S^4}$ metric, and its determinant being ${\gamma ^{WZ}}$ . One must now show the Poincaré invariance of the bosonic constraints

$\left( {{\varphi _0},{\varphi _i}} \right)$

and the supersymmetric covariance of the fermionic constraint $\psi$ under the $SL(2,\Re )$ transformation of $\left( {\not B,\not \Sigma } \right)$ and $\left( {\phi ,\chi } \right)$ corresponding to the $SO(2)$ fermionic field rotation holds. Then one gets

$\left( {\begin{array}{*{20}{c}}{\not B}\\{\not \Sigma }\end{array}} \right) = {V^{ - 1}}\left( {\begin{array}{*{20}{c}}B\\{{{\not \Sigma }^{ - 1}}}\end{array}} \right) + \left( {\begin{array}{*{20}{c}}{{\Omega ^3}}\\{ - \,{\Omega ^1}}\end{array}} \right)$

and

${\left( {{\Omega ^l}} \right)^i} \equiv {\varepsilon ^{ijk}}\widetilde \theta \not \prod _i^{ * \dagger }{\tau _l}\,\not \partial \theta$

with $V$ being an $SL(2,\Re )/SO(2)$ matrix satisfying

$V = {e^{\Phi /2}}\left( { - {\chi ^l} \cdot {e^{ - \phi }}} \right)$

and transforms as

$\delta V \to \Lambda V{\rm O}{(\Lambda )^{ - 1}}$

with

$\Lambda = \left( {\begin{array}{*{20}{c}}a&b\\c&d\end{array}} \right) \in SL(2,\Re )$

and

$ad - bc = 0$

and ${\rm O}(\Lambda )$ being an $SO(2)$ transformation satisfying

${\rm O}{(\Lambda )^{ - 1}} = \left( {\begin{array}{*{20}{c}}{\cos \lambda }&{\sin \lambda }\\{ - \sin \lambda }&{ - \cos \lambda }\end{array}} \right) \in SO(2)$

and

${V^{ - 1}} = {e^{\phi /2}}\left( {\begin{array}{*{20}{c}}{{e^{ - \phi }}}&0\\\chi &1\end{array}} \right) \to {\rm O}(\Lambda )\left( {\begin{array}{*{20}{c}}{{\Omega ^3}}\\{ - {\Omega ^1}}\end{array}} \right)$

with ${\tau _2}$ rotation $\theta \to {\rm O}(\Lambda )\theta$ .

To prove D3-brane self-duality, we must consider

$\begin{array}{c}{{\not P}_M} = \not P - \left( {{{\not \Sigma }^i}\frac{{\not \partial {F_{01}}\left( {\prod ,\widetilde \theta } \right)}}{{\not \partial \prod _0^M}} + {{\not B}^i}\frac{{\not \partial C_{ij}^{(2)}\left( {\prod ,\widetilde \theta } \right)}}{{\not \partial \prod _o^M}}} \right) - \\\left( {\frac{1}{2}{\varepsilon ^{ijk}}C_{ij}^{(2)}\frac{{\not \partial {F_{0i}}\left( {\prod ,\widetilde \theta } \right)}}{{\not \partial \prod _0^M}} + \frac{{\not \partial }}{{\not \partial \prod _0^m}}\sqrt { - {G_{\mu \nu }}} {C^{(4)}}\left( {\prod ,\widetilde \theta } \right)} \right)\end{array}$

while noting that all terms in the above expression and $\not P$ itself are invariant under Poincaré duality transformations. So, ${\not P_M}$ , the conjugate of $\not P$ , is also likewise invariant, hence,

$\frac{{\not \partial }}{{\not \partial \prod _0^M}}\sqrt { - {G_{\mu \nu }}} {C^{(4)}}\left( {\prod ,\widetilde \theta } \right)$

reduces to

$\begin{array}{c}\left( {{{\not \Sigma }^i}\frac{{\not \partial {F_{0i}}}}{{\not \partial \prod _0^M}} + \frac{1}{2}{\varepsilon _{ijk}}{{\not B}^i}\frac{{\not \partial {C^{{{(2)}^{jk}}}}}}{{\not \partial \prod _0^M}}} \right) \cdot {{\not \Sigma }^i}\widetilde {\theta \,}{\Gamma _M}{\tau _3}\,{{\not \partial }_i}\theta = \left( {{{\not B}^i},{{\not \Sigma }^i}} \right) \cdot \\\left( {\begin{array}{*{20}{c}}{\widetilde {\theta \,}{\Gamma _M}{\tau _1}{{\not \partial }_i}\theta }\\{\widetilde \theta \,{\Gamma _M}{\tau _3}\,\not \partial \theta }\end{array}} \right) = \widetilde {\theta \,}\Gamma {\tau _{{0^i}}}{{\not \partial }_i}\widetilde \theta \end{array}$

where

$\tau _0^i = {\not \Sigma ^i}{\tau _3} + {\not B^i}{\tau _1}$

holds. In terms of differential forms,

$\not P \equiv \frac{{\not \partial {L^{DBI}}}}{{\not \partial \prod _0^M}}$

reduces to

$\begin{array}{c}{C^{{{(2)}^{0,i}}}}\frac{{\not \partial {F_{0i}}}}{{\not \partial \prod _0^M}} + \frac{{\not \partial }}{{\not \partial \prod _0^M}}\sqrt { - {G_{\mu \nu }}} {C^{(4)}} \to \frac{1}{2}{\left[ { - \left( {\widetilde \theta {\Gamma _M}{\tau _{\left[ {3d\theta } \right]}}\,d\theta } \right)\left( {\widetilde \theta \not \prod {\tau _1}d\theta } \right)} \right]_3} + \\{\left[ {\frac{{\not \partial {C^{(4)}}}}{{\not \partial \prod _0^M}}} \right]_3} = \frac{1}{2}{\left[ { - \widetilde {\theta \,}{\Gamma _M}{\tau _{\left[ {3d\theta } \right]}}d\theta \left( {\widetilde \theta \not \prod {\tau _1}d\theta } \right)} \right]_3} + {\left[ {\frac{{\not \partial }}{{\not \partial \prod _0^M}}\left( {{C^{(4)}} + \frac{1}{2}{\Omega _1}\,{\Omega _3}} \right)} \right]_3}\end{array}$

where ${\left[ {} \right]_3}$ represents a spatial 3-form coefficient of $\left[ {} \right]$ , and given the Poincaré invariance of ${\tau _1}$ and ${\tau _3}$ under $\theta$ rotation, one can finish the proof by utilizing the gauge invariance of $\not P$ and by using the identity

$\Xi = \left[ {{C^{(4)}} + \frac{1}{2}{\Omega _1}\,{\Omega _3}} \right]$

Diffeomophically, $\not B$ and $\not \Sigma$ essentially appear in the irreducible representation of $SO(2)$ , and thus, ${\varphi _0}$ and ${\varphi _i}$ also have Poincaré invariance. Now, the supersymmetric covariance of the fermionic constraints with the above $\not P$ is

$\begin{array}{c}\psi = {\pi _\theta } + {{\not P}_M}\left( {\widetilde \theta \,{\Gamma ^M}} \right) - \left( {{{\not \Sigma }^i}\frac{{\not \partial {F_{0i}}}}{{\not \partial \widetilde \theta }} + \frac{1}{2}{\varepsilon _{ijk}}{{\not B}^i}\frac{{\not \partial {C^{{{(2)}^i}}}}}{{\not \partial \widetilde \theta }}} \right) - \\\left( {{C^{{{(2)}^{0i}}}}\frac{{\not \partial {F_{0i}}}}{{\not \partial \widetilde \theta }} + \frac{{\not \partial \sqrt { - {G_{\mu \nu }}} {C^{(4)}}}}{{\not \partial \widetilde \theta }}} \right)\end{array}$

where one finds by Gaussian functional reduction

$\left( {{{\not \Sigma }^i}\frac{{\not \partial {F_{0i}}}}{{\not \partial \widetilde \theta }} + \frac{1}{2}{\varepsilon _{ijk}}{{\not B}^i}\frac{{\not \partial {C^{{{(2)}^{jk}}}}}}{{\not \partial \widetilde \theta }}} \right) = \frac{1}{2}\widetilde {\theta \,}{\Gamma _{\tau _0^i}}{\not \partial _i}\theta \cdot \widetilde \theta \,\Gamma - \widetilde {\theta \,}{\Gamma _{\tau _0^i}}{\not \prod _i}$

and

${C^{(2)}}\frac{{\not \partial {F_{0i}}}}{{\not \partial \widetilde \theta }} + \frac{{\not \partial }}{{\not \partial \widetilde \theta }}\sqrt { - {G_{\mu \nu }}} {C^{(4)}} = {\left[ { - \frac{1}{2}\left( {\widetilde \theta \not \prod {\tau _1}d\theta } \right)\left\{ {\left( {\widetilde \theta \,{\Gamma _M}{\tau _3}d\widetilde \theta } \right)\frac{1}{2}\widetilde \theta \,{\Gamma ^M} - \widetilde \theta \not \prod {\tau _3}} \right\} + \frac{{\not \partial \Xi }}{{\not \partial \widetilde \theta }}} \right]_3}$

Now, given that ${\pi _\theta }$ transforms as

${\pi _\theta } \to {\pi _\theta }{\rm O}{(\Lambda )^{{T_3}}}$

where ${T_3}$ is the D3-brane tension, the fermionic expression $\psi$ covariantly transforms as

$\psi \to \psi \,{\rm O}{(\Lambda )^{{T_3}}}$

Now I must exhibit the self-duality of the D3-brane Hamiltonian, given the gauge field, as usual, ${A_\mu }$ , acting on the automorphic group of $Ad{S_4} \times {S^4}$ , and the D = 3 metric ${g_{ij}}$ replaced by the D3-brane worldvolume 4-D metric $\gamma _{ij}^{D3}$ , expressed in terms of brane coordinates $\left( {\chi ,\theta } \right)$ . Note, for any function $R(p,q)$ on the super-Kahler phase space,

$\delta R = - \left[ {R,\not W} \right]$

with

$\not W = \lambda \int {{d^3}} \sigma \sqrt {\gamma _{ij}^{D3}} \left[ {\frac{1}{2}\frac{{\not \Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }}D_{il}^{ - 1}\frac{{\not \Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }} + \frac{1}{2}{A_i}{D^{ij}} + {\pi _\theta }\frac{{i{\tau _2}}}{2}\theta } \right]$

where $D_{il}^{ - 1}$ is a tensor acting on a vector as such:

$D_{il}^{ - 1} \equiv {({\widetilde \Delta ^{ - 1}})_i}^k{\nabla ^j}{\eta _{jkl}} = {\eta _{ijk}}{\nabla ^k}({\widetilde \Delta ^{ - 1}})_l^j$

with

${\eta _{ikl}} = {\varepsilon _{jkl}}\sqrt {\gamma _{ij}^{D3}}$

being the covariant anti-symmetric constant tensor, and is the inverse of

${D^{jk}} = {\eta ^{jlk}}{\nabla _l} = {\nabla _l}{\eta ^{jlk}}$

In the projective geometry of $Ad{S_4} \times {S^4}$ , we then have

$\left\{ {\begin{array}{*{20}{c}}{D_{im}^{ - 1}{D^{mk}} = {\rm O}_i^k(\nabla )}\\{{\rm O}_i^k(\nabla ) = \delta _i^k - {\nabla _i}({\Delta ^{ - 1}}){\nabla ^k}}\\{{D^{im}}D_{mk}^{ - 1} = {\rm O}_k^i(\nabla )}\end{array}} \right.$

noting that ${\rm O}_i^k(\nabla )$ longitudinally projects out the components of the covariant derivative ${\nabla _i}$ .

Now, in the D3-brane 4-dimensional curved worldspace, the Laplacian operator $(\widetilde \Delta )_j^i$ is given by

$(\widetilde \Delta )_j^i = \Delta \delta _j^i - R_j^i{T_3}$

with $R_j^i$ being the Ricci tensor: one then derives, by use of the Atiyah–Singer index theorem , that $\not W$ generates the desired ${A_i}$ duality transformation for the gauge field, and generates the $SO(2)$ rotation of $\theta$ :

$\delta {A_l} = \lambda \left( {{{\widetilde \Delta }^{ - 1}}} \right)_l^k{\nabla ^j}{\varepsilon _{jkm}}\not \Sigma = D_{lm}^{ - 1}\left( {\lambda \frac{{\not \Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }}} \right)$

with

$\left\{ {\begin{array}{*{20}{c}}{\delta \not \Sigma = - \lambda {\varepsilon ^{ijk}}{{\not \partial }_j}{A_k}}\\{\delta \theta = \lambda \frac{{i{\tau _2}}}{2}\theta }\\{\delta {\pi _\theta } = - {\pi _\theta }\lambda \frac{{i{\tau _2}}}{2}}\\{\delta \chi = 0}\\{\delta \not P = 0}\end{array}} \right.$

and so we obtain

$\left\{ {\begin{array}{*{20}{c}}{\delta \not B = \lambda {{\not \Sigma }^{ * \dagger }}}\\{\delta {{\not \Sigma }^{ * \dagger }} = - \lambda \not B}\end{array}} \right.$

where

${\not \Sigma ^{ * \dagger }} = \not \Sigma - \sqrt {\gamma _{ij}^{D3}} \left( {{\Delta ^{ - 1}}} \right)\left( {{\nabla _{lm}}\frac{{\not \Sigma }}{{\sqrt {\gamma _{ij}^{D3}} }}} \right)$

So: to sum all this up, the D3-brane self-dual Hamiltonian action is invariant under linear $SL(2,\Re )$ transformation:

$\left( {\begin{array}{*{20}{c}}{\not B}\\{\not \Sigma }\end{array}} \right) \to \Lambda \left( {\begin{array}{*{20}{c}}{\not B}\\{\not \Sigma }\end{array}} \right)$

and rotations of $\left( {\theta ,{\pi _\theta }} \right)$ , by

$\left\{ {\begin{array}{*{20}{c}}{{\rm O}(\Lambda )\theta }\\{{\pi _\theta }{\rm O}{{(\Lambda )}^{{T_3}}}}\end{array}} \right.$

and non-linear transformation of the background $\phi$ and $\chi$ . This finishes the proof of the self-duality of the D3-brane Hamiltonian action.

Indeed: If in other sciences we should arrive at certainty without doubt and truth without error, it behooves us to place the foundations of knowledge in mathematics. ~ Roger Bacon