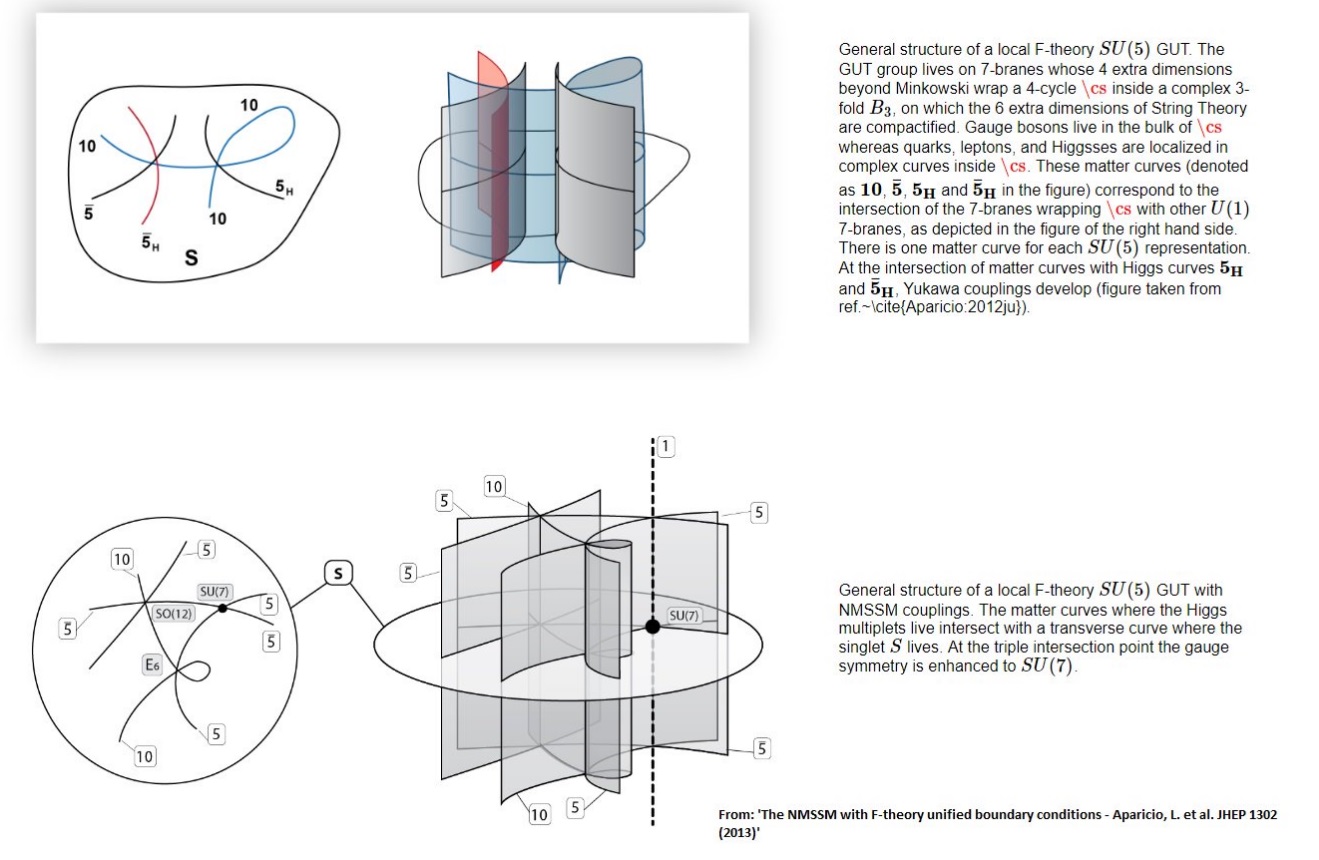
There is a deep way to geometrically engineer Yang-Mills GUT models from a coupling of Chern-Simons theory to Heterotic string theory via B-model topological twisting and double T-dualizing on the base of the elliptic fibration of F-theory where the orbifold delta function plays an essential role. The topological gauge part of the SYM Chern-Simons Lagrangian is given by:
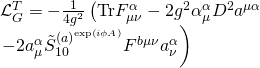
where ![]() is the orbifold delta function:
is the orbifold delta function:
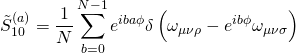
with ![]() the dilaton and
the dilaton and ![]() are terms derived from the D5-brane backreaction and such that varying the orbifold function with respect to the Type-IIB action induces orbifold-compactifications that locally inject 4-D gauge actions written as:
are terms derived from the D5-brane backreaction and such that varying the orbifold function with respect to the Type-IIB action induces orbifold-compactifications that locally inject 4-D gauge actions written as:
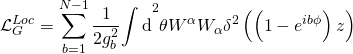
Hence, the Ramond-Ramond coupling is given by:
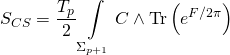
and since for Type-IIB, ![]() is odd, the potential for the Type-IIB theory compactified on a Calabi-Yau threefold
is odd, the potential for the Type-IIB theory compactified on a Calabi-Yau threefold ![]() takes the form:
takes the form:
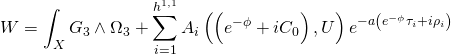
where the translational, rotational, and Chern-Simons 3-form of gauge-class:
![]()
are respectively:
![]()
![]()
and
![]()
which are derived by varying the Lagrangian density:
![]()
with respect to ![]() and
and ![]() . This yields us the crucial NS-NS field equations:
. This yields us the crucial NS-NS field equations:
![]()
![]()
Noting that the Einstein-Hilbert terms in the metaplectic Riemann-Cartan formalism constitute systolic algebraic 1-forms as well as a super-Lie-algebraic dual of the Lorentz connection:
![]()
more precisely:
![]()
it follows that the corresponding dual-field strength is the 2-form Kähler torsion:
![]()
with curvature form:
![]()
The Poisson-Lie duality allows us to add Chern-Simons forms, and by gauging the super-Poincaré group, we get the desired Mielke-Baekler theory that solves for the Einstein-Cartan Lagrangian:
![]()
Now, combining the Chern-Simons VEV equations:
![]()
and:
![]()
by modularity, we get the torsion and Riemann-Cartan curvature, respectively:
![]()
![]()
where ![]() is the Picard constant:
is the Picard constant:
![]()
and:
![]()
is the CS-Witten term. Now, coupling to matter fields, we get the torsion condition:
![]()
and the Riemann-Cartan form reduces to:
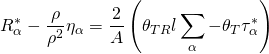
which yields the 4-D action for ![]() :
:
![]()
In order to show the CS-H Yang-Mills GUT construction modulo a Teichmüller orbifold, note that by the F/M-theory duality, flux-compactification yields moduli-stabilization via double-Higgsing and solving the Yukawa coupling integral-equation:
![]()
Now, taking the Hodge dual gives us the Hodge-Fukaya form:
![]()
and realizing that the elliptic fibration induces a Calabi-Yau potential as a polynomial in ![]() that yields via Kaluza-Klein reduction and
that yields via Kaluza-Klein reduction and ![]() -backreaction PBS conditions on the string spectrum to derive the SYM Green’s function and then coupling the Hodge-Fukaya form to the Heterotic action in the Einstein-frame:
-backreaction PBS conditions on the string spectrum to derive the SYM Green’s function and then coupling the Hodge-Fukaya form to the Heterotic action in the Einstein-frame:
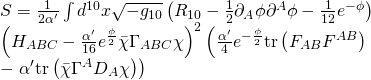
where ![]() is the 3-flux form:
is the 3-flux form:
![]()
and ![]() is the Chern-Simons 3-form given by:
is the Chern-Simons 3-form given by:
![]()
gives an action that is isomorphic for the class of Lorentzian manifolds to the path integral of F-theory, and visually, it gives rise to the following picture:
where the Type-IIB action is:
![]()
with the Neveu-Schwarz, Ramond-Ramond, and Chern-Simons actions are, respectively:
![]()
![]()
and
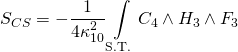
giving us the CS-H Yang-Mills D3-brane GUT model:
The key is the topological coupling of solutions to the Yukawa coupling integral-equation:
![]()
on the orbifolded fibration to:
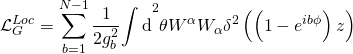
and using the variation-principle with respect to the CS action term:
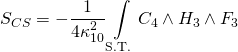
The GUT is hence achieved by solving the monodromy action-equation on the elliptic-curve line-bundle by ![]() -cusp
-cusp ![]() D7-brane intersections on the base with divisors defining the elliptic singularities, where
D7-brane intersections on the base with divisors defining the elliptic singularities, where ![]() is the number of degeneracies of the torus-modulus as a varying function of the RR-C-form and the dilaton, and integrating the exact holomorphic 2-form
is the number of degeneracies of the torus-modulus as a varying function of the RR-C-form and the dilaton, and integrating the exact holomorphic 2-form ![]() :
:
![]()
giving us a K3-class model over an integral basis of 2-cycles ![]() and where the corresponding period integrals elliptic over
and where the corresponding period integrals elliptic over ![]() 1-cycles:
1-cycles:
![]()
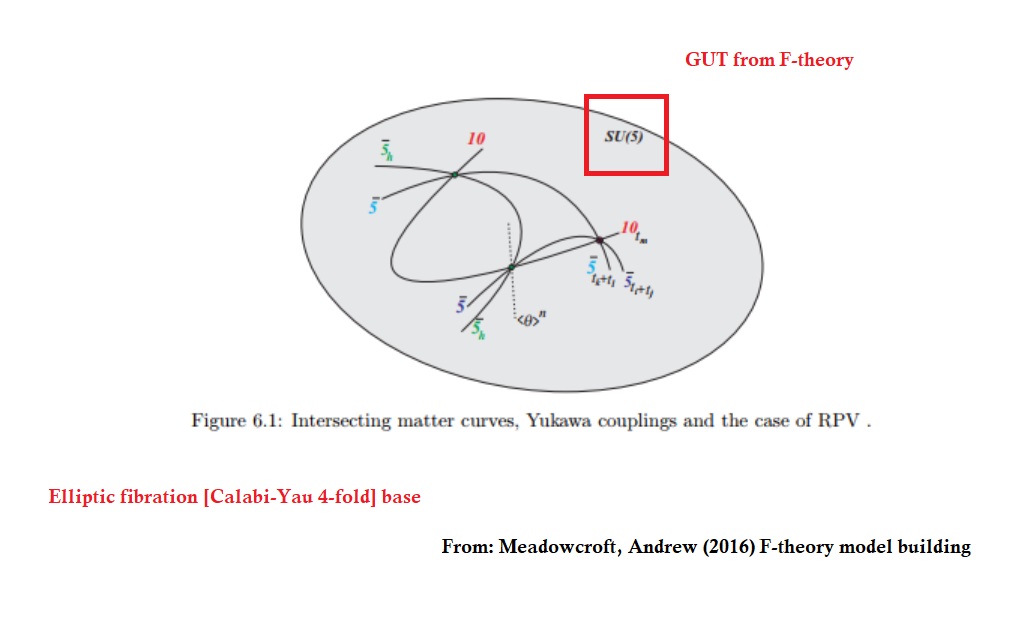
factoring in the base modulus cusp ![]() -terms and summing over divisor points over resolutions of D-7-branes localized on the line degeneracies. Pictorially, we get our desired F/M-GUT as:
-terms and summing over divisor points over resolutions of D-7-branes localized on the line degeneracies. Pictorially, we get our desired F/M-GUT as:
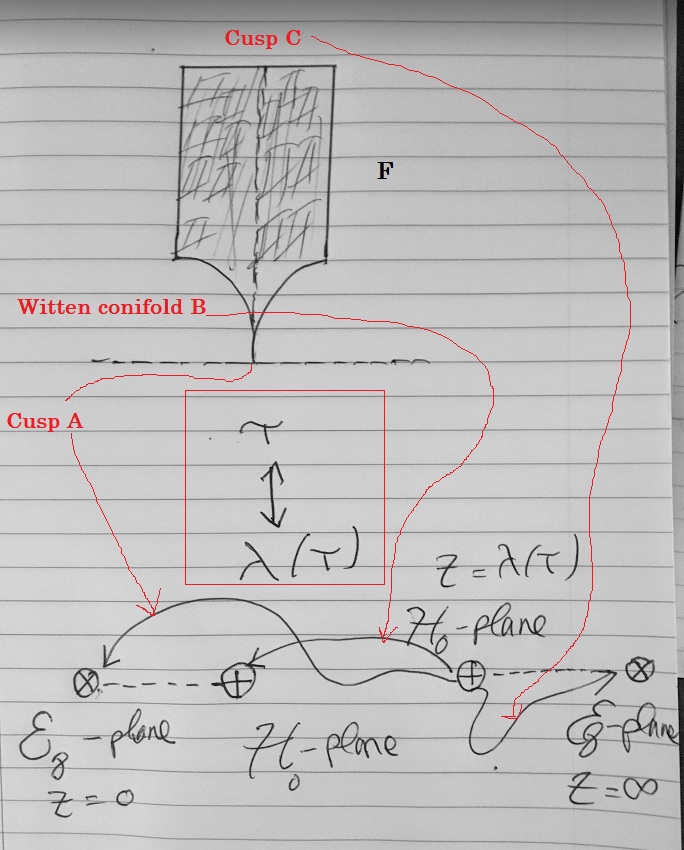
Note that the Hauptmodul-function ![]() maps the fundamental region to the 7-plane geometry via D7-brane backreaction as a function of the Type-IIB Jacobi-term of the
maps the fundamental region to the 7-plane geometry via D7-brane backreaction as a function of the Type-IIB Jacobi-term of the ![]() -plane for:
-plane for:
![]()
guaranteeing moduli stabilization, and by the Heterotic/F-theory duality, topological mirror symmetry twists our fibration to a Calabi-Yau 3-fold such that the period-integrals:
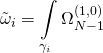
and:
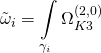
satisfy the Picard-Fuchs differential equations, and by coupling the Einstein-Cartan Lagrangian:
![]()
to the Hodge-Fukaya form:
![]()
we get the B-twist courtesy of the Yukawa coupling integral-equation:
![]()
on the orbifolded fibration, and by mirror symmetry, the A-model deformation and the Fourier-Mukai orbifold-delta functional transform:
![]()
yield us the desired GUT model containing the Standard Model as a proper sub-embedded gauge groupoid variety.