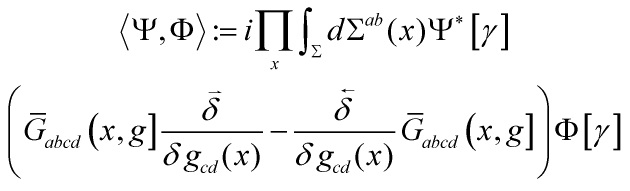We saw how the omega-simplified Wheeler-DeWitt equation:
![]()
with the corresponding scalar product
![]()
which is conserved in ![]() -time by virtue of:
-time by virtue of:
![]()
allowed us to derive what looks like a Hilbert space inner-product, until one looks at the right-hand-side of:
there can be no selection of an intrinsic time functional hence, the non-existence of a suitable Killing-vector follows: this is the ‘Hilbert space problem’ for time. Here, I shall try and recover a notion of time via a Dirac-Schrödinger analysis. The heart of the problem is that at the quantum gravitational and Planck-scales, time disappears both, as a Q-background-parameter and as a GR-dynamical one. To appreciate this Planckian spin on the Wheeler-DeWitt and the quantum mechanical Mandelstam-Tamm time-energy uncertainty-relation problem of time, note that the Hamiltonian reads explicitly, in the geometrodynamical formulation:
with ![]() , and
, and ![]() ,
, ![]() ,
, ![]() respectively are the gravitational constant, the three-dimensional Ricci scalar, and the cosmological constant. And, the coefficients
respectively are the gravitational constant, the three-dimensional Ricci scalar, and the cosmological constant. And, the coefficients ![]() depend on the metric and centrally play the role of a metric on
depend on the metric and centrally play the role of a metric on ![]() , the space of all three-metrics, and it is hyperbolicity at each space point which gives rise to an intrinsic timelike variable.
, the space of all three-metrics, and it is hyperbolicity at each space point which gives rise to an intrinsic timelike variable.
The connection representation yields:
and
![]()
is the field strength tensor corresponding to the complex connection A and ![]() is the metric-independent totally skew-symmetric density of weight
is the metric-independent totally skew-symmetric density of weight ![]() .
.
The important difference between 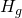 and
and 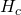 is that
is that 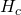 does not contain the Ricci scalar, and contains only terms with functional derivatives and that it is intrinsically complex since A is complex: the philosophical point is that in both formulations there is an absence of any external time parameter in the Wheeler-DeWitt equation!
does not contain the Ricci scalar, and contains only terms with functional derivatives and that it is intrinsically complex since A is complex: the philosophical point is that in both formulations there is an absence of any external time parameter in the Wheeler-DeWitt equation!
Clearly, a necessary condition for the consistency of physics is the recovery of the Schrödinger equation with its ![]() term. One possibility to get
term. One possibility to get ![]() would be to include a matter field with linear momentum into the fundamental Hamiltonian, but at closer inspection, the Mandelstam-Tamm time-energy uncertainty-relation blocks such an option. One can try a recovery via a Born-Oppenheimer expansion with respect to the Planck mass and that’s how complex numbers enter into quantum theory. To show exactly how, express the total state in the form
would be to include a matter field with linear momentum into the fundamental Hamiltonian, but at closer inspection, the Mandelstam-Tamm time-energy uncertainty-relation blocks such an option. One can try a recovery via a Born-Oppenheimer expansion with respect to the Planck mass and that’s how complex numbers enter into quantum theory. To show exactly how, express the total state in the form ![]() for a complex function
for a complex function ![]() and expand
and expand ![]() in powers of the Planck mass. So, the highest order
in powers of the Planck mass. So, the highest order ![]() leads to the condition that
leads to the condition that ![]() must not depend on the matter fields, hence, we get:
must not depend on the matter fields, hence, we get:
![Rendered by QuickLaTeX.com \[\sum\limits_{i,j} {\left( {\frac{{\delta {S_0}}}{{\delta {\phi _i}}}} \right)} \left( {\frac{{\delta {S_0}}}{{\delta {\phi _j}}}} \right){g_{ij}}\left( \phi \right) = 0\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ef719d2e6db303b661cd6bebff429972_l3.png)
with ![]() a positive definite quadratic form and it is crucial for the recovery of time that
a positive definite quadratic form and it is crucial for the recovery of time that ![]() not depend on the fields
not depend on the fields ![]() . Now, the next order
. Now, the next order ![]() yields the Hamilton-Jacobi equation for gravity:
yields the Hamilton-Jacobi equation for gravity:
![]()
and is equivalent to Einstein’s field equations and hence corresponds to the description of a semi-classical gravitational background.
The crucial step happens in the next order ![]() where the time-dependent Schrödinger equation can be recovered provided that
where the time-dependent Schrödinger equation can be recovered provided that ![]() is chosen to be real with a negligible imaginary part. This corresponds to the choice of a complex wave function at this order, yet this has an ad-hoc-ness touch to it. We must introduce a wave functional
is chosen to be real with a negligible imaginary part. This corresponds to the choice of a complex wave function at this order, yet this has an ad-hoc-ness touch to it. We must introduce a wave functional
![]()
satisfying
![]()
with ![]() the matter part of the Hamiltonian density. Noting that
the matter part of the Hamiltonian density. Noting that
![]()
is the functional Tomonaga-Schwinger equation for matter fields propagating in the classical background given by
![]()
with ![]() a multi-fingered time parameter and it seems that the emergence of a time parameter in the semiclassical limit is due to the fact that time is not an absolute entity but is inextricably entangled with the dynamical evolution of quantum subsystems in the cosmological sense. Hence, the choice of an imaginary solution for
a multi-fingered time parameter and it seems that the emergence of a time parameter in the semiclassical limit is due to the fact that time is not an absolute entity but is inextricably entangled with the dynamical evolution of quantum subsystems in the cosmological sense. Hence, the choice of an imaginary solution for ![]() in
in
![]()
would lead to a diffusion-type of equation instead of the Schrödinger equation
![]()
In quantum gravity scenarios, this is interpreted as describing a Euclidean spacetime
and the problem now is that superpositions of WKB states would not allow the recovery of the Schrödinger equation as expressed above.
The superposition
![]()
which is a ‘real’ solution to the Wheeler-DeWitt equation at order ![]() , does not lead to:
, does not lead to:
![]()
So let us try the derivation in the connection representation, since it is apriori complex and so the wave functional is a holomorphic functional of the connection. However, note we still the problem that only a special WKB-state allows one to derive the Schrödinger equation for matter fields. So, expanding ![]() in powers of the gravitational constant and plugging the state into the Wheeler-DeWitt equation with the Hamiltonian given by
in powers of the gravitational constant and plugging the state into the Wheeler-DeWitt equation with the Hamiltonian given by
we find that ![]() does not depend on matter fields and moreover it obeys the Hamilton-Jacobi equation:
does not depend on matter fields and moreover it obeys the Hamilton-Jacobi equation:
and since the momentum conjugate to ![]() ,
, ![]() is replaced by
is replaced by
![]()
without ‘![]() ‘, in the Schrödinger representation, the momentum is given by:
‘, in the Schrödinger representation, the momentum is given by:
![]()
The next order ![]() yields the functional Schrödinger equation for the wave functional
yields the functional Schrödinger equation for the wave functional
![]()
![]()
with:
Some philosophical points are in order now.
- Note, the Hamiltonian density
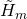 is equal to
is equal to 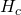 as determined by the Hamilton-Jacobi equation except for the last three
as determined by the Hamilton-Jacobi equation except for the last three 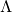 -dependent terms in the
-dependent terms in the 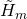 -equation above, which arise due to the presence of the third functional derivatives in
-equation above, which arise due to the presence of the third functional derivatives in
The problem is: this does not happen in the geometrodynamical formulation.
- Moreover, there is the issue of the complex nature of the connection. Equation:
![]()
can be written as a functional Schrödinger equation if there is an appropriate region of configuration space with a time functional ![]() that can be introduced such that the following holds:
that can be introduced such that the following holds:
where this time functional, however, is in general complex, and since the wave functional is a holomorphic functional in any order of approximation, its derivative with respect to τ is fully determined by its derivative with respect to the real part of τ which may thus serve to play the role of physical time. However, the semiclassical expansion will include an expansion of the ‘reality-conditions’, which, in highest order, leads to a restriction of the original configuration space onto a subspace!
- Also, the above derivation of the Schrödinger equation did not depend on expanding the classical Hamiltonain constraint to second order around a chosen classical background after which we truncate the constraint as a condition on the wave functional. Hence, the holomorphicity of the wave functional enabled one to identify a certain functional of the imaginary part of the trace part of A with physical time. The gravitational part alone then satisfies a Schrödinger equation with respect to this time variable. This is the main difference here, which I only attempt to derive such an equation for quantum matter fields in a semiclassical gravitational background.
Here is the problem: how, then, can we justify the use of a single state 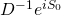 in the derivation of the Schrödinger equation?
in the derivation of the Schrödinger equation?
Decoherence cannot help due to phase-transitional chaotic dynamics coupled with the Mandelstam-Tamm time-energy uncertainty-relation problem of time! To appreciate this point, note that in the geometrodynamic approach, a superposition is of the form:
![]()
where ![]() and
and ![]() satisfy the time-dependent Schrödinger equation and
satisfy the time-dependent Schrödinger equation and ![]() with the sign-reversed time-parameter.
with the sign-reversed time-parameter. ![]() depends only on the three-metric,
depends only on the three-metric, ![]() depends on the three-metric as well as on all nongravitational fields. Hence, these degrees of freedom contained in
depends on the three-metric as well as on all nongravitational fields. Hence, these degrees of freedom contained in ![]() are inaccessible. So we must focus on the reduced density matrix for the gravitational part:
are inaccessible. So we must focus on the reduced density matrix for the gravitational part:
![]()
Decoherence then occurs if in the total density matrix
so we have, instead of the superposition
![]()
the many-WKB components
![]()
and each component has its own WKB time. One would then expect decoherence to explain why the second sum in the total density matrix:
![]()
becomes negligible after integrating out the irrelevant degrees of freedom.
However, we run into the problem of the occurrence-of-anomalies: that is, Weyl fermions in an external electromagnetic background acquire an anomaly leading to the violation of gauge invariance
and this is intimately connected with the emergence of a Berry phase functional ![]()
![]()
with ![]() the vector potential and
the vector potential and
![]()
is a super-gauge potential defined on the potential-configuration space. One can restore gauge invariance but one loses Lorentz invariance if one replaces the electromagnetic field momentum according to
![]()
and this introduces complex numbers into the electromagnetic field Hamiltonian.
However, the Standard Model of gauge theories does not possess such anomalies and such Lorentz anomalies do not exist in four spacetime dimensions
therefore, as far as canonical quantum gravity and planck-scale quantum spacetime in three space dimensions, we have No-Go-Theorems!
Towards a solution. Torsion is the key?!
The action for a Dirac field in an external gravitational field is complex if torsion is nonvanishing and leads to a complex Hamiltonian and thus produce a nontrivial Berry phase
The only justification for
![]()
is that it gives rise to ![]() -states in quantum gravity if the diffeomorphism group is not connected: that is, if
-states in quantum gravity if the diffeomorphism group is not connected: that is, if
![]()
is non-vanishing. One would therefore expect, in analogy to ordinary quantum theory, that the wave-functional transforms according to a one-dimensional, irreducible, representation of
![]()
and the ![]() -sectors labelled by elements of the group of homomorphisms of
-sectors labelled by elements of the group of homomorphisms of ![]() into
into ![]() .
.
This is crucial: the emergence of a ![]() parameter is well known from Yang-Mills theories. Thus,
parameter is well known from Yang-Mills theories. Thus, ![]() states are labelled by the elements of
states are labelled by the elements of ![]() . In the connection approach to quantum gravity, the situation is homologous.
. In the connection approach to quantum gravity, the situation is homologous.
So, instead of taking the gauge group as the starting point, we take an alternative view and focus on the topological properties of the physical configuration space, ![]() , of the theory. In the Yang-Mills case this is the space of vector potentials modulo
, of the theory. In the Yang-Mills case this is the space of vector potentials modulo ![]() , while in gravity this is the space of Riemannian metrics, RiemΣ, on Σ modulo diffeomorphisms. Quantum theory on nontrivial configuration spaces has the property that
, while in gravity this is the space of Riemannian metrics, RiemΣ, on Σ modulo diffeomorphisms. Quantum theory on nontrivial configuration spaces has the property that ![]() structures emerge if the first fundamental group
structures emerge if the first fundamental group ![]() is nonvanishing. The quantum mechanical propagator
is nonvanishing. The quantum mechanical propagator ![]() of a system can be expressed as a sum of propagators
of a system can be expressed as a sum of propagators ![]() with each
with each ![]() , the paths lie in the same homotopy class. Thus
, the paths lie in the same homotopy class. Thus
![]()
In the functional Schrödinger equation wave functionals are cross sections of a complex bundle over ![]() which gives rise to a connection over
which gives rise to a connection over ![]() precisely in the way as in
precisely in the way as in
![]()
One considers flat connections only since there is no hint of a super-connection with non-vanishing curvature in the framework of the Wheeler-DeWitt equation.
Both viewpoints can be unified since the symmetry group acts freely on RiemΣ, and the ![]() parameter can be directly connected with the nontrivial structure of the configuration space itself. In quantum gravity, though, Diff(Σ) does not act freely because of the existence of isometries, yet can be removed when one goes to the extended superspace.
parameter can be directly connected with the nontrivial structure of the configuration space itself. In quantum gravity, though, Diff(Σ) does not act freely because of the existence of isometries, yet can be removed when one goes to the extended superspace.
The deep question of course is: which three-manifolds Σ can lead to a nontrivial 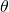 structure?
structure?
Since
![]()
for orienting preserving diffeomorphisms, there is no such structure.
The next deep question is: might the presence of a 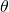 structure be the reason why one can focus consistently on complex solutions to the Wheeler-DeWitt equation and, moreover, to only one WKB component
structure be the reason why one can focus consistently on complex solutions to the Wheeler-DeWitt equation and, moreover, to only one WKB component 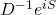 in the semiclassical approximation?
in the semiclassical approximation?
If ![]() and if the group is represented by a one-dimensional, irreducible, representation, the superposition
and if the group is represented by a one-dimensional, irreducible, representation, the superposition
![]()
will not belong to the class of allowed quantum states: a No-Go Theorem.
Now, in three spacetime dimensions, with spatial sections ![]() characterized by the metric:
characterized by the metric:
![]()
so the WheelerDeWitt equation reads:
![]()
and the minisuperspace analogue of
![]()
is here played by the permutation group of bi-scale factors, which has only two one-dimensional, irreducible, representations.
Hence, semiclassical solutions are of the form:
![]()
for S is a solution to the Hamilton-Jacobi equation:
![]()
However, these states are not eigenstates of the permutation operator: hence, one has to superpose two semiclassical states of the form
![]()
to arrive at states which are either symmetric or antisymmetric under the action of the permutation group.
Such superpositions, however, do not allow one to recover the Schrödinger equation for matter fields. This is possible only if one chooses one of the two solutions
and note the above ‘solutions’ is an exact solution of
![]()
Thus, the superposition of the two states 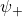 and
and 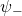 does not allow the derivation of the Schrödinger equation
does not allow the derivation of the Schrödinger equation
- The situation different in the connection representation,and that is because the wave functional is defined on a space of connections, and thus one has, in addition to the diffeomorphism group, an
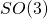 gauge group, and thus one has
gauge group, and thus one has 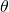 states in analogy to the Yang-Mills case independent of whether the action of the diffeomorphism group is represented or not. These states exist due to
states in analogy to the Yang-Mills case independent of whether the action of the diffeomorphism group is represented or not. These states exist due to
![]()
thus, the wave functional transforms under a large gauge transformation with winding number n as:
![]()
But, superpositions like
![]()
are thus forbidden if one assumes, in analogy to the Yang-Mill case, that physical states are eigenstates of the operator which generates large gauge transformations
A way out is for the field momentum to change according to:
![]()
and includes the gravitational constant, with
![]()
A deeper understanding of the derivation of the Schrödinger equation from quantum gravity was attempted in order to recover the disappeared time in the Wheeler-DeWitt equation as well as in the context of the Mandelstam-Tamm time-energy uncertainty-relation problem of time. The ![]() parameter does not lead to any selection principle amongst possible WKB solutions, and the
parameter does not lead to any selection principle amongst possible WKB solutions, and the ![]() -superselection rule is not and cannot be caused by decoherence in any dynamical way: there is no notion of quantum-environment that allows any decoherence of different
-superselection rule is not and cannot be caused by decoherence in any dynamical way: there is no notion of quantum-environment that allows any decoherence of different ![]() eigenstates. Hence, both, the structures of the configuration space in the geometrodynamical and in the connection dynamical formulations are inadequate to recover and thus solve the problem-of-time in physics, at any scale.
eigenstates. Hence, both, the structures of the configuration space in the geometrodynamical and in the connection dynamical formulations are inadequate to recover and thus solve the problem-of-time in physics, at any scale.