A Weyl-Plebanski 7-D Embedding of General Relativity

By George Shiber Thursday, December 1, 2016Friday, October 26, 2018 In Mathematical Physics, Mathematics, Philosophy Of Physics, Philosophy Of Science, Physics, Super String Theory Einsteinian Space-Time, General Relativity

I will derive an isomorphism between a Cartan-3-form Weyl-theory in 7-D and general relativity in Plebanski formulation and discuss the depth and impact. Basically, that the 4D Lagrangian:

$\begin{array}{l}{L_{4D}}/{\phi ^4} = {B^i}{F^i} - \frac{1}{2}{M^{ij}}{B^j}\\ + 2\mu \left( {\det \left( {\tilde {\rm I} + {\phi ^2}M} \right) - {\phi ^3}} \right)vo{l_\Sigma }\end{array}$

is an exact description of general relativity, where ${L_{4D}}$ is given by:

$\begin{array}{l}{L_{4D}} = {\phi ^4}{B^i}{F^i} + \frac{{{\phi ^2}}}{2}{B^i}{B^i} + \\3{\phi ^3}{\left( {\det (X)} \right)^{1/3}}vo{l_\Sigma }\end{array}$

and the metric-volume form implicitly defining $vo{l_\Sigma }$ , namely, $vo{l_C}$ , is:

$\begin{array}{l}vo{l_C} = \frac{{{\phi ^3}}}{6}{\varepsilon ^{ijk}}{W^i}{W^j}{W^k}\\{\left( {\det (X)} \right)^{1/3}}vo{l_\Sigma }\end{array}$

with the 3-form $C$ on a 7-D manifold $M$ is explicitly defined by the ${G_2}$ –holomorphic metric:

${g_C}\left( {\xi ,\eta } \right)vo{l_C} = \frac{1}{6}{i_\xi }C \wedge {i_\eta }C \wedge C$

with the action:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

Such holomorphic 3-forms in 7-D are analytically related to the exceptional group ${G_2}$ , which can be interpreted as the subgroup of ${\rm{GL}}\left( 7 \right)$ that metaplectically stabilizes generic 3-forms.

Any generic 3-form $C$ on a 7-D manifold $M$ defines a metric ${g_C}$ explicitly given by the formula:

${g_C}\left( {\xi ,\eta } \right)vo{l_C} = \frac{1}{6}{i_\xi }C \wedge {i_\eta }C \wedge C$

where ${g_C}(\xi ,\eta )$ is the metric contraction of two vector fields, $vo{l_C}$ the volume form, and ${i_{\xi ,\eta }}$ is the Hilbert space vector-field insertion operator. Now, the space of generic 3-forms at a point can be identified with the coset

${\rm{GL}}\left( 7 \right)/{G_2}$

and ${g_C}$ as characterized above allows us to embed ${G_2}$ into $SO(7)$ . One can explicitly describe $vo{l_C}$ as a homogeneity of degree 7/3 ${g_C}$ -holomorphic object constructible from the generic 3-form $C$ .

With

${\tilde \varepsilon ^{{a_1}...{a_7}}}$

the completely densitiesed anti-symmetric tensor with values $\pm 1$ , a = 1, . . . , 7,. We have then the 7/3 scalar:

${\tilde \varepsilon ^{{a_1}...{a_7}}}{\tilde \varepsilon ^{{b_1}...{b_7}}}{\tilde \varepsilon ^{{c_1}...{c_7}}}{C_{{a_1}{b_1}{c_1}}}...{C_{{a_7}{b_7}{c_7}}}$

whose cube root is a multiple of $vo{l_C}$ . Dynamically, for $C$ , we get the action:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

which entails the Euler-Lagrange equations:

$dC = {\lambda ^ * }C$

and $^ * C$ is the ${g_C}$ -defined Hodge dual of $C$ , yielding:

$vo{l_C} = - \left( {1/7} \right)C{ \wedge ^ * }C$

Real 3-forms satisfying

$dC = {\lambda ^ * }C$

have Riemannian signature metrics ${g_C}$ and possess ${G_2}$ structure.

Crucial:

$dC = {\lambda ^ * }C$

entails that $^ * C$ is closed and ${g_C}$ is Einsteinian with non-zero scalar curvature.

One can therefore relate the theory determined by the action:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

to 4-D general relativity since the action is dimensionally reduced on ${S^3}$ , and that is an isomorphism restricted to Weyl curvatures smaller than Planckian, which is the desired regime where we can trust GR as a classical theory.

One begins with GR in higher dimensions and carries a dimensional reduction to 4 dimensions. The main claim here is that 4D GR analytically arises as the dimensional reduction of the theory defined by:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

of 3-forms in 7D, and such a theory is a dynamical theory of 3-forms, not the metrics. The natural question, besides the deeply curious fact that 4D GR admits a lift to a theory of seemingly such a different type, one may ask: wherein lies the theoretical and foundational utility? The key is that the dimensionally reduced theory is GR with non-zero cosmological constant, and it is directly related to the size of the KK ${S^3}$ . As the 5D Kaluza-Klein theory transforms the electric charge into a dynamically determinate quantity via a spontaneous compactification mechanism, in this context, the 4D cosmological constant becomes in theory determinable by the dynamics of the extra dimensions, and the dimensionally reduced theory is the Riemannian signature GR.

Without loss of generality, one can work under the assumption that the group ${\rm{SU}}(2)$ acts freely on $M$ , thus importing on $M$ the structure of an ${\rm{SU}}(2)$ principal bundle over a 4-dimensional base ${{\rm{M}}_B}$ . Staying local over regions of ${{\rm{M}}_B}$ , we parametrise fiber points as such:

$g \in {\rm{SU}}(2)$

and the group action being the right action of ${\rm{SU}}(2)$ on itself and:

$\bar m = {g^{ - 1}}dg$

the Maurer-Cartan one-forms on ${\rm{SU}}(2)$ . To proceed with the main claim, let $\bar A$ be an ${\rm{SU}}(2)$ connection on ${{\rm{M}}_B}$ – that is, a 2×2 anti-Hermitian matrix valued 1-form on ${{\rm{M}}_B}$ , with:

$A = {g^{ - 1}}\bar Ag$

its lift into the total space of the bundle. It follows that:

$W = \bar m + A$

is the connection 1-form in the total space of the bundle. Hence, we have:

$F: = dW + WW$

which is a 2-form that is purely horizontal:

$F = {g^{ - 1}}\bar Fg$

where:

$\bar F = d\bar A + \bar A\bar A$

is the curvature of the connection 1-form on the base.

Key: an ${\rm{SU}}(2)$ invariant 3-form on X can be written as

$C = {\rm{Tr}}\left( {\phi {{\bar m}^3} + A\bar m + B\bar m} \right) + c$

with $A$ and $B$ being lifts to the bundle of Lie algebra valued 1- and 2-forms on the base ${{\rm{M}}_B}$ respectively, and this entails that in order for 4D GR to analytically arise as the dimensional reduction of the theory defined by:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

of 3-forms in 7D, the correct parametrization of $C$ must be:

$C = - 2{\rm{Tr}}\left( {\frac{1}{3}{\phi ^3}{W^3} + \phi WB} \right) + c$

with:

$\left\{ {\begin{array}{*{20}{c}}{\phi \in {\Lambda ^0}\left( M \right)}\\{c \in {\Lambda ^3}\left( M \right)}\end{array}} \right.$

One can easily compute to get:

$\begin{array}{l}dC = - 2{\rm{Tr}}\left( {{\phi ^2}} \right.d\phi {W^3} + \left( {{\phi ^3}F + B} \right){W^2}\\ + \left( {d\phi B + \phi {d_A}B} \right)W + \left. {\phi FB} \right) + dc\end{array}$

where the lift to the bundle of the covariant derivative of Lie algebra-valued 2-form $\bar B$ with respect to the connection $\bar A$ is given by:

${d_A}B = {g^{ - 1}}\left( {d\bar B + \bar A\bar B} \right)g$

and the trace-identity property gives us:

$\begin{array}{l}\frac{1}{2}\int_M {CdC = \int_{{\rm{SU}}(2)} { - \frac{2}{3}} } {\rm{Tr}}\left( {\bar m} \right) \times \\\int_M { - 2} {\rm{Tr}}\left( {{\phi ^4}\bar B\bar F + \left( {{\phi ^2}/2} \right)\bar B\bar B} \right)\\ + {\phi ^3}dc\end{array}$

So, the dimensional reduction of the first term in:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

which is topological, is the BF theory with a $\Lambda$ -term, coupled to the scalar and 3-form fields, thus the dimensional reduction of the topological theory is itself topological, allowing us to recover the Lagrangian of the topological BF theory with the $\Lambda$ term.

Let’s analyze the dimensional reduction of the second term in:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

note, this is a no-derivative term, hence only the following potential fields:

$\left\{ {\begin{array}{*{20}{c}}\phi \\B\\c\end{array}} \right.$

can be changed by it. Also, since:

entails that the 3-form field $c$ is conjugate to $\phi$ , one can treat it as a constant and set $c$ to zero. The volume form corresponding to:

$C = - 2{\rm{Tr}}\left( {\frac{1}{3}{\phi ^3}{W^3} + \phi WB} \right) + c$

can be derived by decomposing all matrix-valued fields in terms of the ${\rm{SU}}(2)$ generators:

${\tau ^i} = - \left( {i/2} \right){\sigma ^2}$

with ${\sigma ^i}$ the Pauli matrices. We can deduce now the following:

$C = \frac{{{\phi ^3}}}{6}{\varepsilon ^{ijk}}{W^i}{W^j}{W^k} + \phi {W^i}{B^i}$

where $C$ in canonical form is:

$C = \frac{1}{6}{\varepsilon ^{ijk}}{e^i}{e^j}{e^k} + {e^i}{\Sigma ^i}$

with ${\Sigma ^i}$ the basis of anti-self-dual 2-forms:

$\left\{ {\begin{array}{*{20}{c}}{{\Sigma ^1} = {e^{45}} - {e^{67}}}\\{{\Sigma ^2} = {e^{46}} - {e^{75}}}\\{{\Sigma ^3} = {e^{47}} - {e^{56}}}\end{array}} \right.$

We now note that the metric corresponding to our theory defined by the above action is:

$ds_C^2 = {\sum\nolimits_{a = 1}^7 {\left( {{e^a}} \right)} ^2}$

Keep in mind the number 7. The metric for:

$C = \frac{{{\phi ^3}}}{6}{\varepsilon ^{ijk}}{W^i}{W^j}{W^k} + \phi {W^i}{B^i}$

we note first the Urbantke formula:

${g_\Sigma }\left( {\xi ,\eta } \right)vo{l_\Sigma } = - \frac{1}{6}{\varepsilon ^{ijk}}{i_\xi }{\Sigma ^i} \wedge {i_\eta }{\Sigma ^j} \wedge {\Sigma ^k}$

is the metric on the base from:

${g_C}\left( {\xi ,\eta } \right)vo{l_C} = \frac{1}{6}{i_\xi }C \wedge {i_\eta }C \wedge C$

hence the 7-D character of the Urbantke formula. So, the 2-forms ${B^i}$ can always be parametrised as:

${B^i} = {\sqrt X ^{ij}}{\Sigma ^j}$

we then have

${B^i} \wedge {B^j} = - 2{X^{ij}}vo{l_\Sigma }$

Substituting the parametrisation:

${B^i} = {\sqrt X ^{ij}}{\Sigma ^j}$

into:

$C = \frac{{{\phi ^3}}}{6}{\varepsilon ^{ijk}}{W^i}{W^j}{W^k} + \phi {W^i}{B^i}$

the 3-form reduces to:

$C = \rho \left( {\frac{1}{6}{\varepsilon ^{ijk}}{e^i}{e^j}{e^k} + {e^i}{\Sigma ^i}} \right)$

where:

$\left\{ {\begin{array}{*{20}{c}}{\rho = {{\left( {\det \left( X \right)} \right)}^{1/4}}}\\{{e^i} = \frac{\phi }{\rho }{{\sqrt X }^{ij}}{W^j}}\end{array}} \right.$

this yields the variant metric:

$\begin{array}{l}ds_C^2 = {\phi ^2}{W^i}\frac{{{X^{ij}}}}{{{{\left( {\det \left( X \right)} \right)}^{1/3}}}}{W^j} + \\{\left( {\det \left( X \right)} \right)^{1/6}}ds_\Sigma ^2\end{array}$

whose volume-form is:

$\begin{array}{l}vo{l_C} = \frac{{{\phi ^3}}}{6}{\varepsilon ^{ijk}}{W^i}{W^j}{W^k} \cdot \\{\left( {\det \left( X \right)} \right)^{1/3}}vo{l_\Sigma }\end{array}$

Collecting all of our data so far, the picture is getting clear: one can write the dimensionally reduced 4D Lagrangian on the ansatz:

$C = - 2{\rm{Tr}}\left( {\frac{1}{3}{\phi ^3}{W^3} + \phi WB} \right) + c$

divided by the volume of the fiber, giving us:

$\begin{array}{l}{L_{4D}} = {\phi ^4}{B^i}{F^i} + \frac{{{\phi ^2}}}{2}{B^i}{B^i} + \\3{\phi ^3}{\left( {\det \left( X \right)} \right)^{1/3}}vo{l_\Sigma }\end{array}$

which is the Lagrangian of type-BF theory plus a potential for the $B$ field,

and this is a 4D gravity theory

To reduce to GR, we rewrite the last term in:

$\begin{array}{l}{L_{4D}} = {\phi ^4}{B^i}{F^i} + \frac{{{\phi ^2}}}{2}{B^i}{B^i} + \\3{\phi ^3}{\left( {\det \left( X \right)} \right)^{1/3}}vo{l_\Sigma }\end{array}$

via an auxiliary matrix field, yielding:

$\begin{array}{l}6{\left( {\det \left( X \right)} \right)^{1/3}}vo{l_\Sigma } = - {H^{ij}}{B^i}{B^j}\\ + 2\mu \left( {\det \left( H \right) - 1} \right)vo{l_\Sigma }\end{array}$

such a way of rewriting the last term in:

$\begin{array}{l}{L_{4D}} = {\phi ^4}{B^i}{F^i} + \frac{{{\phi ^2}}}{2}{B^i}{B^i} + \\3{\phi ^3}{\left( {\det \left( X \right)} \right)^{1/3}}vo{l_\Sigma }\end{array}$

allows us to reduce the 4D Lagrangian to:

$\begin{array}{l}{L_{4D}}/{\phi ^4} = {B^i}{F^i} - \frac{1}{2}{M^{ij}}{B^j}\\ + 2\mu \left( {\det \left( {\tilde {\rm I} + {\phi ^2}M} \right) - {\phi ^3}} \right)vo{l_\Sigma }\end{array}$

Setting:

$\phi H = \tilde I + {\phi ^2}M$

And here is the Plebanskian point:

the constraint 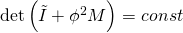$\det \left( {\tilde I + {\phi ^2}M} \right) = const$ expanded in powers of 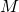$M$ is the constraint 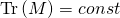${\rm{Tr}}\left( M \right) = const$ , and this is isomorphic to General Relativity in Plebanski formulation

hence:

$\begin{array}{l}{L_{4D}}/{\phi ^4} = {B^i}{F^i} - \frac{1}{2}{M^{ij}}{B^j}\\ + 2\mu \left( {\det \left( {\tilde {\rm I} + {\phi ^2}M} \right) - {\phi ^3}} \right)vo{l_\Sigma }\end{array}$

describes GR.

One now reparametrise ${L_{4D}}/{\phi ^4}$ via:

${M^{ij}} = {\Psi ^{ij}} + \frac{1}{3}\Lambda \left( \Psi \right)$

with ${\Psi ^{ij}}$ the tracefree part of ${M^{ij}}$ and $\Lambda \left( \Psi \right)$ is the function gotten by imposing the constraint in the second line of:

$\begin{array}{l}{L_{4D}}/{\phi ^4} = {B^i}{F^i} - \frac{1}{2}{M^{ij}}{B^j}\\ + 2\mu \left( {\det \left( {\tilde {\rm I} + {\phi ^2}M} \right) - {\phi ^3}} \right)vo{l_\Sigma }\end{array}$

Solving, we get the following:

$\begin{array}{l}{\left( {1 + \frac{{\Lambda {\phi ^2}}}{3}} \right)^3} - \frac{3}{2}\left( {1 + \frac{{\Lambda {\phi ^2}}}{3}} \right) \cdot \\{\phi ^4}{\rm{Tr}}\left( {{\Psi ^2}} \right) + {\phi ^6}\det \left( \Psi \right) = {\phi ^3}\end{array}$

and:

$\frac{{\Lambda \left( \Psi \right)}}{3} = \frac{{\phi - 1}}{{{\phi ^2}}} + \frac{\phi }{2}{\rm{Tr}}\left( {{\Psi ^2}} \right) + O\left( {{\Psi ^3}} \right)$

So, the isomorphism follows from the fact that the Plebanski Lagrangian, which is:

${L'_{Pleb}} = M_p^2\left( {{B^i}{F^i} - \frac{1}{2}\left( {{\Psi ^{ij}} + \frac{\Lambda }{3}} \right){B^i}{B^j}} \right)$

has a dimensionless field ${B^i}$ that describes, at the Planck-mass scale, the metric via Urbantke formula:

${g_\Sigma }\left( {\xi ,\eta } \right)vo{l_\Sigma } = - \frac{1}{6}{\varepsilon ^{ijk}}{i_\xi }{\Sigma ^i} \wedge {i_\eta }{\Sigma ^j} \wedge {\Sigma ^k}$

Hence:

$\left\{ {\begin{array}{*{20}{c}}\Psi \\\Lambda \end{array}} \right.$

are dimensionless, and $\Psi$ is the anti-self-dual part of the Weyl-curvature measured in Planck units and so is isomorphic to GR at all scales.

Note also, the dimensionless $\Lambda$ is the cosmological constant measured in Planck units, and is a negligibly small number $\Lambda$ ∼ 10−120 that embodies the cosmological constant problem.

The theory:

$\begin{array}{l}{L_{4D}}/{\phi ^4} = {B^i}{F^i} - \frac{1}{2}{M^{ij}}{B^j}\\ + 2\mu \left( {\det \left( {\tilde {\rm I} + {\phi ^2}M} \right) - {\phi ^3}} \right)vo{l_\Sigma }\end{array}$

yields a negligible cosmological constant for values of radius of compactification $\phi$ close to unity, thus we get:

$\phi = - 1 = \frac{\Lambda }{{3M_P^2}}$

Hence, stating our result, the dimensionally reduced theory:

$S\left[ C \right] = \frac{1}{2}\int_M C \wedge dC + 6\lambda vo{l_C}$

gives a 4D gravity theory that in the regime of Weyl curvatures $\Psi \ll M_P^2$ is indistinguishable from GR in Plebanski formulation, as mathematically expressed by:

${L_{4D}} \approx {L_{Pleb}}$

which is remarkable and reflects compactified extra dimensions: that is why I said “Keep in mind the number 7”. The main difference between our model here and Kaluza-Klein compactifications of supergravity where a N-D manifold with a ${G_2}$ structure is used for compactifying 11-D supergravity down to 4D, here we described gravity itself using 3-forms, which is not an object that exist in addition to the metric: it is the only object that exists. The metric, and in particular the 4D metric, is defined by the 3-form via:

${g_C}\left( {\xi ,\eta } \right)vo{l_C} = \frac{1}{6}{i_\xi }C \wedge {i_\eta }C \wedge C$

Many details and open questions remain to be addressed: however, that such an isomorphism exists with an [in]direct connection to compactifications of supergravity points to something deep foundationally in theoretical physics and quantum-gravity programs must heed such a lesson.