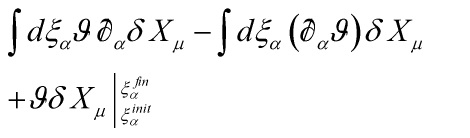Sign up with your email address to be the first to know about new products, VIP offers, blog features & more.

M-Theory and how the Quantum Worldsheet Knows 4-D Spacetime Physics

By Posted on In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Physics, Super String Theory, Witten Theory ,
M-Theory

Here, I will demonstrate how M-theory implies that the string worldsheet quantum theory ‘knows’ all about four-dimensional physics. Start with the Dp-action:

    \[S_p^D = \, - {T_p}\int\limits_{{\rm{worldvolumes}}} {{d^{p + 1}}} \xi \frac{{\not D_{\mu \nu }^{susy}L}}{{{{\not \partial }_{{v_a}}}}}{e^{ - {\Phi _{bos}}}}{\rm{de}}{{\rm{t}}^{1/2}}G_{ab}^{\exp \left( {H_{p + 1}^{{\rm{array}}}} \right)}\]

4-dimensionality entails that the mass of a Dp-brane can be derived as:

    \[{T_p}{e^{ - {\Phi _{bos}}}}\prod\limits_{i = 1}^p {\left( {2\pi nR} \right)} \]

and by T-dualizing in the

    \[{X^p}\]

direction and factoring the dilaton, the dual is hence:

    \[\begin{array}{c}({T_p}\left( {2\pi \sqrt {\alpha '} } \right){e^{ - {\Phi _{bos}}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_p}} \right)} = \\{T_{p - 1}}{e^{ - \Phi _{bos}^{1/2}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_{p - 1}}} \right)} \end{array}\]

By matrix world-volume integral reduction on

    \[S_p^D = \, - {T_p}\int\limits_{{\rm{worldvolumes}}} {{d^{p + 1}}} \xi \frac{{\not D_{\mu \nu }^{susy}L}}{{{{\not \partial }_{{v_a}}}}}{e^{ - {\Phi _{bos}}}}{\rm{de}}{{\rm{t}}^{1/2}}G_{ab}^{\exp \left( {H_{p + 1}^{{\rm{array}}}} \right)}\]

the Polyakov action for the string is hence:

    \[{S^p} - \frac{1}{{4\pi \alpha '}}\int {{d^2}} \sigma \sqrt { - \gamma } {\gamma ^{ab}}{\not \partial _a}{X^\mu }{\not \partial _b}{X^\nu }{G_{\mu \nu }}\]

with {X^\mu }\left( {\tau ,\sigma } \right) the embedding of the string in target space, {\gamma _{ab}} the worldsheet metric, and {G_{\mu \nu }} the spacetime metric.

Now, the variation, through all Einstein-indices, of the action with respect to {\gamma ^{\rho \sigma }} is then:

    \[\delta {S^p} = - \frac{T}{2}\int {{d^2}} \xi \left\{ \begin{array}{l} - \frac{1}{2}\sqrt { - \gamma } {\gamma _{\sigma \rho }}\delta {\gamma ^{\sigma \rho }}{\gamma ^{\alpha \beta }}{h_{\alpha \beta }}\\ + \sqrt { - \gamma } {h_{\sigma \rho }}\delta {\gamma ^{\sigma \rho }}\end{array} \right\}\]

with

    \[\frac{{\delta {S^p}}}{{\delta {\gamma ^{\rho \sigma }}}} = - \frac{T}{2}\int {{d^2}} \xi \sqrt { - \gamma } \left\{ {{h_{\rho \sigma }} - {\gamma _{\rho \sigma }}{\gamma ^{\alpha \beta }}{h_{\alpha \beta }}} \right\}\]

and with equation of motion (EOM):

    \[{h_{\rho \sigma }} = \frac{1}{2}{\gamma _{\rho \sigma }}{\gamma ^{\alpha \beta }}{h_{\alpha \beta }}\]

after taking the determinant, the following holds:

    \[{\gamma ^{\alpha \beta }}{h_{\alpha \beta }} = 2\frac{{\sqrt { - h} }}{{\sqrt { - \gamma } }}\]

and inserting into the Polyakov action yields:

    \[{S^p}\left| {_{EOM}} \right. = - T\int {{d^2}} \xi \sqrt { - h} = {S_{NG}}\]

with {S_{NG}} the Nambu-Goto action for the string:

    \[{S_{NG}} = - T{\int {\rm{d}} ^3}\sigma \sqrt { - g} \]

hence, the functional derivative of the Polyakov Lagrangian with respect to the derivative of the dynamical field is

    \[\frac{{\delta {L_P}}}{{\delta \,{{\not \partial }_\alpha }{X^\mu }}} = - \frac{T}{2}\sqrt { - \gamma } 2{\gamma ^{\alpha \beta }}{\not \partial _\beta }{X^\upsilon }{\eta _{\mu \nu }}\]

giving us the Euler-Lagrange equations:

    \[{\not \partial _\alpha }\left( {\sqrt { - \gamma } {\gamma ^{\alpha \beta }}{{\not \partial }_\beta }{X_\mu }} \right) = 0\]

Thus, the strings obey a wave equation

as can be seen by the Laplacian equation:

    \[\left\{ {\begin{array}{*{20}{c}}{{\nabla ^2}{X^\mu } = 0}\\{{\nabla ^2}f \equiv \frac{1}{{\sqrt \gamma }}{{\not \partial }_a}\left( {\sqrt \gamma {\gamma ^{ab}}{{\not \partial }_b}f} \right)}\end{array}} \right.\]

It follows then that the renormalization Lie-equation for the sigma-model on the string worldsheet entails

    \[{\beta _{\mu \nu }} = \frac{{{\rm{d}}{G_{\mu \nu }}}}{{{\rm{dlog}}\Lambda }} = \alpha '{R_{\mu \nu }} + O\left( {{{\alpha '}^2}} \right) = 0\]

So, from

    \[\begin{array}{c}({T_p}\left( {2\pi \sqrt {\alpha '} } \right){e^{ - {\Phi _{bos}}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_p}} \right)} = \\{T_{p - 1}}{e^{ - \Phi _{bos}^{1/2}}}\prod\limits_{i = 1}^{p - 1} {\left( {2\pi {R_{p - 1}}} \right)} \end{array}\]

the Einstein vacuum field equation is encoded in the quantum structure of the worldsheet theory as characterized by

    \[{\vartheta _\mu }\left( u \right){\vartheta _\nu }\left( v \right) = \lambda _{\mu \nu }^\rho \frac{{{\vartheta _\rho }}}{{{{\left( {u - v} \right)}^\# }}} + ...\]

with \vartheta satisfying:

Untitledqerg

Therefore, the β-function equation gives a definition of the stress-energy tensor for the worldsheet theory

    \[{\beta ^{\mu \nu }} = {T^{\mu \nu }} = \frac{{\delta \,{\Gamma _{eff}}}}{{\delta {G_{\mu \nu }}}}\]

with

    \[{e^{ - {\Gamma _{eff}}}} = \exp \left( {\int {{d^2}\sigma {G_{\mu \nu }}{T^{\mu \nu }}} } \right)\]

By holographic renormalization, it follows that the worldsheet quantum theory knows all about 4-D spacetime physics

as attested by

    \[\frac{d}{{{d_{{\sigma _p}}}}}\int\limits_{{\rm{worldvolumes}}}^p {{e^{H_{p + 1}^{{\rm{array}}}}}} + \underbrace {\sum\limits_{{\sigma _p}}^D {{{\left( {S_p^D} \right)}^{ - H_{p + 1}^{{\rm{array}}}}}} }_{{\rm{topologies}}}\]

eq57ept

previously

previously

Flux Compactifications of String Theory and Kähler/Calabi–Yau manifolds
up next

up next

String Field Theory, 4-D Space-Time and the Superstring
RELATED
F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory
Posted on
Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds
Posted on
The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory
Posted on