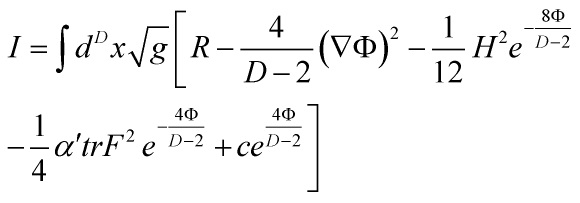All viable quantum cosmological field theories must solve the cosmological singularity problem, and analogously with quantum gravity theories must presuppose non-commutative spacetime and quantum geometry, consistency requirements on same said theories indicate no-singularity cosmology scenarios: this is an excellent representative read.
In this post, I will analyze how non-singular cosmology emerges in heterotic string theory
Consider the inverse string tension ![]() in the Einstein frame with effective string action in D-dimensions:
in the Einstein frame with effective string action in D-dimensions:
with
![]()
and
![]()
with the heterotic string action being, generically:
and
![]()
![]()
Noting that the field ![]() is the antisymmetric tensor field,
is the antisymmetric tensor field, ![]() the background spacetime gauge field. The constant c is the central charge deficit:
the background spacetime gauge field. The constant c is the central charge deficit:
![]()
in the heterotic and superstring theories.
The field 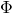 is the fundamental scalar field of string theory, the dilaton. Moreover, note that
is the fundamental scalar field of string theory, the dilaton. Moreover, note that 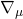 in the above effective string action in D-dimensions is the covariant spacetime derivative in D-dimensions
in the above effective string action in D-dimensions is the covariant spacetime derivative in D-dimensions
and crucial substitutions in the EEA with respect to:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}\Phi \\{{g_{\mu \nu }}}\\{{B_{\mu \nu }}}\\{{A_{a\mu }}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-35f1dc1b19bccaba850589deab7a65f0_l3.png)
gives us:
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{{T_{\mu \nu }} = \frac{8}{{D - 2}}{{\left( {\bar \nabla \Phi } \right)}^2}\left. {{g_{\mu \nu }}} \right] - \frac{1}{2}{e^{ - \frac{{8\Phi }}{{D - 2}}}}\left[ {H_{\mu \nu }^2 - \frac{1}{6}{H^2}{g_{\mu \nu }}} \right]}\\{ - \frac{{\alpha '}}{2}{e^{ - \frac{{4\Phi }}{{D - 2}}}}\left[ {2F_{\mu \nu }^2 - \frac{1}{2}tr{F^2}{g_{\mu \nu }}} \right]}\\{ - c{e^{\frac{{4\Phi }}{{D - 2}}}}{g_{\mu \nu }}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-242a92573728d19bdda743106f264461_l3.png)
as well as:
![]()
and:
![]()
Now, since I can set
, an exact solution with an homogeneous and isotropic Robertson-Walker metric can be given by
![Rendered by QuickLaTeX.com \[\begin{array}{l}d{s^2} = - d{t^2} + a{\left( t \right)^2}\left[ {\frac{{d{r^2}}}{{1 - k{r^2}}}} \right. + {r^2}\\\left. {\left( {d{\theta ^2} + {{\sin }^2}\theta d{\varphi ^2}} \right)} \right]\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a40e6f44f8300de3b8540fbd33801b58_l3.png)
with non-vanishing components:
![]()
with:
![]()
so that
![]()
reduces to:
![]()
with:
![]()
thus allowing us to derive:
![]()
given maximal spatial symmetry.
Since in a homogeneous universe, all fields are essentially functions of time, equation:
![]()
has a solution via the ansatz:
![]()
with ![]() a homogeneous scalar field.
a homogeneous scalar field.
Here is the deep pivot – we can infer that:
![]()
can be derived from:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{H^2}_j^i = h\left( t \right)\delta _j^i}\\{{H^2}_0^0 = 0}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bc4fb195ea4852fb86fba09e6a344923_l3.png)
with
![]()
Given the fact that
then from:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{{T_{\mu \nu }} = \frac{8}{{D - 2}}{{\left( {\bar \nabla \Phi } \right)}^2}\left. {{g_{\mu \nu }}} \right] - \frac{1}{2}{e^{ - \frac{{8\Phi }}{{D - 2}}}}\left[ {H_{\mu \nu }^2 - \frac{1}{6}{H^2}{g_{\mu \nu }}} \right]}\\{ - \frac{{\alpha '}}{2}{e^{ - \frac{{4\Phi }}{{D - 2}}}}\left[ {2F_{\mu \nu }^2 - \frac{1}{2}tr{F^2}{g_{\mu \nu }}} \right]}\\{ - c{e^{\frac{{4\Phi }}{{D - 2}}}}{g_{\mu \nu }}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-242a92573728d19bdda743106f264461_l3.png)
it follows that:
![]()
implying that the field equations:
![]()
are solvable obeying the restriction:
![]()
and the tensor ![]() is completely determined by solutions to:
is completely determined by solutions to:
![]()
and
![]()
Thus, the right-hand side in equations:
![]()
and
![]()
yield
![]()
hence we have the no-singular cosmology terms:
![Rendered by QuickLaTeX.com \[\begin{array}{l}T_j^i = \left[ {2{{\left( {\bar \nabla \Phi } \right)}^2} - \frac{1}{4}} \right.{e^{ - 4\Phi }}h - \\\frac{{\alpha '}}{4}{e^{ - 2\Phi }}\left. {\left( {f - {f_0}} \right) - c{e^{2\Phi }}} \right]\delta _j^i\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5eceab23f4872dccc5c18441e93b053a_l3.png)
![]()
and thus, a common property with all quantum gravity theories:
![Rendered by QuickLaTeX.com \[\begin{array}{l}T_0^0 = 4\left[ {\frac{1}{2}{{\left( {\bar \nabla \Phi } \right)}^2} + {{\dot \Phi }^2}} \right] + \\\frac{1}{4}{e^{ - 4\Phi }}h + \frac{3}{4}\alpha '{e^{ - 2\Phi }}\left( {f - {f_0}} \right) - \\c{e^{2\Phi }}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-fab30eefa6166fd0b526f57eb7e0ecc0_l3.png)
with
![]()
Therefore, substituting uniformly with respect to
and
, the scalar equation:
![]()
reduces to:
![]()
which is a coupled non-linear second order differential equations: let’s look at its behavior at ‘t = 0’.
We have for any field ![]() , the following:
, the following:
![]()
![]()
![]()
![]()
![]()
Let me sum the philosophical depth now
- There is no trace of any ‘big-bang’ initial singularity and without violating the general singularity theorems in classical General Relativity, since the strong energy condition, which is sufficient for the existence of the initial singularity, is avoided by a choice of c within an allowed interval determined by IC and BC.
- Also, we have: even though
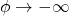 and
and 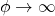 ,
, 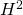 and
and 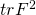 vanish in this limit.
vanish in this limit. - The dynamics of the evolution of the theory fleshed in this post, and it is representative, depend only on the existence of the fields F and H. So the Lagrangian density is:
![]()
with
![]()
the effective potential. Thus, again, implying a non-singular cosmological scenario!
In turn, to torture the physicists