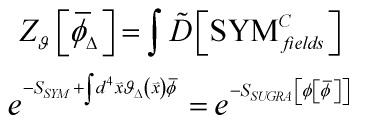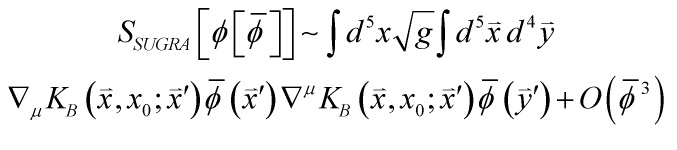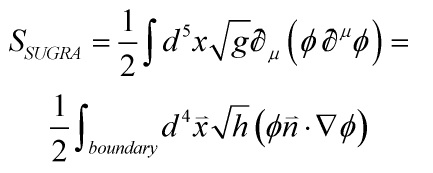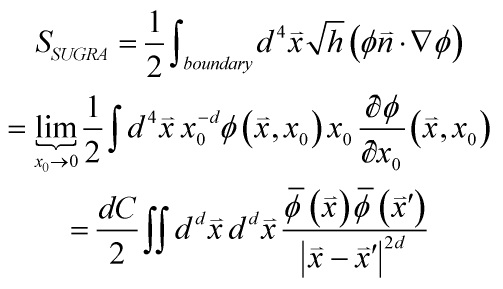String Theory on AdS and Super-Yang–Mills Conformal Field Theory: the Witten Map

By George Shiber Tuesday, July 12, 2016Saturday, August 17, 2019 In Cosmology, Grand Unification Physics, M Theory, Mathematical Physics, Mathematics, Physics, Super String Theory, Supersymmetry, Witten Theory AdS/CFT Duality, holographic principle

The equivalence between string-theory on $Ad{S_5}$ -space and 4-D N = 4 super-Yang–Mills conformal field theory is one of the deepest equivalences in physics, mainly due to the fact that the gauge theory lives on the worldvolume of a stack of D3-branes, which is equivalent to living on the boundary of $Ad{S_5}$ . Throat holographic decoupling is hence essential for extracting the right bulk geometry and boundary topology and that decoupling is mediated by the Witten prescription AdS/CFT-mapping:

And that is what I will expand upon here. This is an excellent introduction to super-Yang–Mills conformal field theory. But first, here is a schematic representation of the AdS/CFT duality:

${\left\langle {T\left\{ {\exp \left( {\int {{d^d}x\,{J_{4D}}(x)\vartheta (x)} } \right)} \right\}} \right\rangle _{CFT}} = {\not Z_{AdS}}\left[ {\underbrace {\lim }_{boundary}J\,{w^{\Delta - d + k}} = {J_{4D}}} \right]$

or more informatively:

${\left\langle {{e^{\int {{d^4}x\,{\phi _{(0)}}(x)\vartheta (x)} }}} \right\rangle _{CFT}} = {\not Z_{{\rm{String}}}}\left\langle {{r^{\Delta - d}}\phi {{(x,r)}_{\left| {_{r = 0}} \right.}} = {\phi _{(0)}}(x)} \right\rangle$

where $\phi (x,r)$ is the ‘bulk-field‘, $r$ the radial coordinate that is dual to the renormalization group in the boundary theory, with:

${\phi _{(0)}}(x) \equiv {r^{\Delta - d}}\phi {(x,r)_{\left| {_{r = 0}} \right.}}$

and $r = 0$ in the CFT boundary of AdS with ${\phi _{(0)}}(x)$ coupled to $\vartheta (x)$

The left-hand-sides are the vacuum expectation value of the time-ordered exponential of the operators over CFT; the right-hand-sides are the quantum gravity generating functional with the given conformal boundary condition. So, on one side, we have a gauge theory in flat space-time at weak coupling and as the coupling increases, the theory must be described as a string-theory in curved space-time. Moreover, at really strong coupling, gravity can only be interpreted as a Sasaki-Einstein holographic emergent property. Lately and increasingly, in the AdS/CFT setting, the relation of the original theory without gravity and the one with gravity is best, and it looks only, describable in the context of non-commutative (NC) quantum field theory. There are many important reasons to have non-commutativity. Here are three central ones. One, a quantum theory of gravity in the NC setting needs no renormalizability. Second, at the Planck scale, the graviton can be Picard-Lefschetz ‘localized’ even in light of the energy-time Heisenberg uncertainty relation. And thirdly, NC quantum field theories are now necessary in string-theory: one can actually prove that the dynamics of a D-brane in the presence of anti-symmetric fields can only be described in terms of a Moyal-product deformed gauge theory: hence non-commutativity! Given all that, the Seiberg-Witten map is crucial, since it takes one from a commutative gauge field to a non-commutative one, and the effect of such a map gives rise to the NC-parameter ${\theta ^{sw,\alpha \beta }}$ on matter background fields and induces the interactions that are metaplectically quasimorphic to gravity, where $\theta$ is the Poisson tensor and the Moyal product $*$ :

$f * g = fe\frac{i}{2}{\theta ^{ij}}\overleftarrow {\not \partial } \overrightarrow {\,\not \partial } g$

with:

$\left[ {{x^i} * {x^j}} \right] = i{\theta ^{ij}}$

holding.

It is well know that the Heisenberg modes of strings in the horizon geometry stay stuck in the throat and are gravitationally bound to the branes whose backreaction sources are the $Ad{S_5} \times {S^5}$ spacetime,

hence the 10-D flat space SUGRA decouples and isolates the Einstein-Sasaki degrees of freedom.

I will define the bulk-to-boundary propagator:

$^5\bigcirc _L^{b/b} = {K_B}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0};\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right) = {\delta ^{\left( 4 \right)}}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} } \right)$

with $^5\bigcirc _L^{b/b}$ the $Ad{S_5}$ -Laplacian, with the RHS representing a delta string-theory source on the boundary of AdS space. And from a bulk solution:

$\int {{d^4}} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '{K_B}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_{0;}}\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right)\bar \phi \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right) = \phi \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0}} \right)$

one gets the 5-D supergravity action:

Now, by the above 5-D supergravity action and

we get the following:

${S_{SUGRA}}\left[ {\phi \left[ {\bar \phi } \right]} \right]\left| {_{\bar \phi = 0}} \right. = \frac{{{\delta _{SUGRA}}\left[ {\phi \left[ {\bar \phi } \right]} \right]}}{{\delta \bar \phi }}\left| {_{\bar \phi = 0}} \right. = 0$

and given that all terms include more than one field $\bar \phi$ , I can now derive:

$\begin{array}{l}\left\langle {\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)} \right\rangle = \frac{\delta }{{\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)}}\left( { - \frac{{\delta {S_{SUGRA}}}}{{\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)}}{e^{ - {S_{SUGRA}}}}} \right)\left| {_{\bar \phi = 0}} \right. = \\ - \frac{{{\delta ^2}{S_{SUGRA}}}}{{\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)\delta \bar \phi \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)}}\left| {_{\bar \phi = 0}} \right.\end{array}$

I am in a position to consider a free massless scalar field with equation of motion

$^5\bigcirc _L^{b/b}\phi = 0$

with string-theory action:

${S_{SUGRA}} = \frac{1}{2}\int {{d^5}} x\sqrt g {\not \partial _\mu }\phi \,{\not \partial ^\mu }\phi$

Now, the above equation of motion kills one of the field-terms and integrating-by-parts yields the following B-action:

where $h$ is the boundary-metric, and $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} \cdot \nabla$ the component of the gradient normal to the boundary.

Let me unpack now the RHS of the B-action and then take the boundary-limit to zero

Note first that the boundary is defined by a slice of constant ${x_0}$ from the B-action, which is an instrinsic part of any string-theory on any AdS-space. Therefore, we have:

$\left\{ {\begin{array}{*{20}{c}}{\sqrt h = x_0^{ - d}}\\{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} \cdot \nabla = {x_0}\not \partial /{{\not \partial }_{{x_0}}}}\end{array}} \right.$

and so at the boundary, we have:

$\phi \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over n} \cdot \nabla \phi = \phi {x_0}\not \partial \phi /{\not \partial _{{x_0}}}$

Thus, by the Witten prescription AdS/CFT-mapping and the full bulk solution above, we can derive:

${x_0}\frac{{\not \partial \phi }}{{\not \partial {x_0}}}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0}} \right) = {x_0}\int {{d^4}} \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} \frac{{\not \partial {K_B}}}{{\not \partial {x_0}}}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0};\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right)\bar \phi \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right)$

and from the B-action above, we get:

$\frac{{\not \partial {K_B}}}{{\not \partial {x_0}}}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0};\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right) = \frac{{dCx_0^{d - 1}}}{{{{\left( {x_0^2 + {{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^2}} \right)}^d}}} - \frac{{dC2x_0^{d + 1}}}{{{{\left( {x_0^2 + {{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^2}} \right)}^{d + 1}}}}$

The denominators in the above, in the limit ${x_0} \to 0$ , become negligible and crucially:

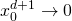$x_0^{d + 1} \to 0$ is faster than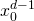 $x_0^{d - 1}$

Therefore, the first term dominates yielding:

${x_0}\frac{{\not \partial {K_B}}}{{\not \partial {x_0}}}\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} ,{x_0};\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right){ \to _{{x_0} \to 0}}\frac{{dCx_0^d}}{{{{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^{2d}}}}$

so, I can use:

to derive the 2-point correlator of the Witten prescription AdS/CFT-mapping:

hence, the 2-point ‘Witten prescription AdS/CFT-mapping‘ function is:

$\left\langle {\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_1}} \right)\vartheta \left( {{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} }_2}} \right)} \right\rangle = \frac{{Cd}}{2}\frac{1}{{{{\left| {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over x} '} \right|}^{2d}}}}$

which is a 2-point correlation function of scalar operators of dimension $\Delta = d$ in a CFT and is equivalent to a CFT-correlation function from classical supergravity. Using the equivalence between string-theory on $Ad{S_5}$ -space and 4-D N = 4 super-Yang–Mills conformal field theory, the AdS/CFT duality, in light of the Witten prescription AdS/CFT-mapping:

yields the desired throat holographic decoupling for the conformal-invariance of 4-D N = 4 super-Yang–Mills field theory in light of that equivalence.