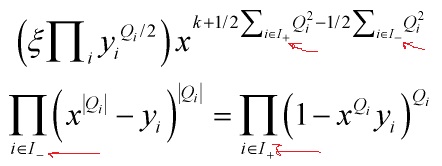In this post, I will discuss the Witten Index in the context of 4-D N = 1 gauge theories on ![]() , a Riemann surface
, a Riemann surface ![]() of genus g times a torus
of genus g times a torus ![]() where in 2-D, the WI is
where in 2-D, the WI is
and by Jeffrey-Kirwan path-integration, we obtain
with ![]() the classical and 1-loop contribution derived from the index of a topological twist on
the classical and 1-loop contribution derived from the index of a topological twist on ![]() via the partition function
via the partition function
and crucially noting that the effective action
![]()
is topological on ![]() . Take 4-D N = 1 gauge theories with a non-anomalous
. Take 4-D N = 1 gauge theories with a non-anomalous ![]()
![]() -symmetry, located on
-symmetry, located on ![]() with a
with a ![]() twist. Given that
twist. Given that ![]() has modulus
has modulus ![]() , the Lagrangian is given by
, the Lagrangian is given by
![]()
with ![]() the supersymmetric Yang-Mills Lagrangian,
the supersymmetric Yang-Mills Lagrangian, ![]() the matter kinetic Lagrangian, and
the matter kinetic Lagrangian, and ![]() superpotential interactions. For Abelian gauge-group factors reasons, we must also include a Fayet-Iliopoulos term
superpotential interactions. For Abelian gauge-group factors reasons, we must also include a Fayet-Iliopoulos term
![]()
where the parameters of the background are the flux
![]()
and flavor flat connection are
![]()
and ![]() lives on a copy of the spacetime
lives on a copy of the spacetime ![]() . Now, define
. Now, define
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{q = {e^{2\pi i\tau }}}\\{x = {e^{iu}}}\\{y = {e^{iv}}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-3ddef4d346104d9eedb79dbeffeb8f3d_l3.png)
Then the semi-classical and one-loop contribution ![]() consists of the following pieces:
consists of the following pieces:
the semi-classical action contribution is from the FI term
![]()
the one-loop determinant for chiral multiplets is
with elliptic functions
![]()
and
So, the one-loop determinant for the off-diagonal vector multiplets is
whereas the vector multiplets contribution along the Cartan generators is
![]()
and the fermionic zero modes on ![]() is
is
![]()
Thus, combining, the final Abelian formula is
and there are no boundary contributions since the integration domain ![]() is compact.
is compact.
In the non-Abelian contexts, W-bosons contributions are factored by re-summing over ![]() and excluding the roots of the associated Baez AEs for which the Vandermonde determinant is zero
and excluding the roots of the associated Baez AEs for which the Vandermonde determinant is zero
Now take ![]() a supersymmetric Yang-Mills-Chern-Simons theory at level
a supersymmetric Yang-Mills-Chern-Simons theory at level ![]() which is equivalent to bosonic Chern-Simons at level
which is equivalent to bosonic Chern-Simons at level ![]() at low energies. The semi-classical and one-loop contribution is
at low energies. The semi-classical and one-loop contribution is
![]()
turning on a background for the topological symmetry. Hence, we can derive
![]()
with the charges of the points at infinity being ![]() and
and ![]()
Given the natural assumptions: ![]() ,
, ![]() and
and ![]()
we get
![]()
where the known and central ![]() is the number of ground states of
is the number of ground states of ![]() Chern-Simons on
Chern-Simons on ![]() .
.
To Witten all roads lead: take  with
with  chiral multiplets of charges
chiral multiplets of charges 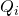 and
and  -charge 1 so one does not face the parity anomalies in the
-charge 1 so one does not face the parity anomalies in the  -symmetry. In the Witten-index context, the semi-classical and one-loop contribution is
-symmetry. In the Witten-index context, the semi-classical and one-loop contribution is
![Rendered by QuickLaTeX.com \[{Z_{{\rm{cl,}}1l}} = {\xi ^{\hat m}}{x^{k\,\hat m\, + \hat t}}{\prod\limits_{i = 1}^N {\left( {\frac{{{x^{{Q_i}/2}}{y_i}^{1/2}}}{{1 - {x^{{Q_i}}}{y_i}}}} \right)} ^{{Q_i}\,\hat m\, + \,{{\hat n}_i}}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-70c6e5bff22b1428d304dfd5af87f216_l3.png)
with ![]() controlling the flavor-symmetries-background for up to one combination that could be reabsorbed into
controlling the flavor-symmetries-background for up to one combination that could be reabsorbed into ![]() , and
, and ![]() controls the background for the topological symmetry, and, in order not to face a gauge-parity anomaly, we insist that the following equivalence holds:
controls the background for the topological symmetry, and, in order not to face a gauge-parity anomaly, we insist that the following equivalence holds:
![]()
To compute the Witten index, set ![]() , and then the poles are at
, and then the poles are at
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{{\hat n}_i} = \hat t = 0}\\{x = 0}\\\infty \end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2d3477689b38fb257db41e09985dbcff_l3.png)
hence the sum over ![]() generates the following
generates the following
with ![]() being the roots of the BaezAEs:
being the roots of the BaezAEs:
![Rendered by QuickLaTeX.com \[{e^{iB}} = \xi {x^k}{\prod\limits_{i = 1}^N {\left( {\frac{{{x^{{Q_i}/2}}y_i^{1/2}}}{{1 - {x^{{Q_i}}}{y_i}}}} \right)} ^{{Q_i}}} = 1\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6b51ce8ea7e0a0eacc01bf8518076a60_l3.png)
hence the index 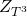 is the Witten index of the theory
is the Witten index of the theory
On the flip-side,
becomes, up to sign-rescaling, the number of solutions to the BaezAEs.
Now, to compute the number of solutions, divide the chiral multiplets into two groups:
![]()
Thus our WI- equation is
Defining the positive numbers
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{n_ + } = \frac{1}{2}\sum\limits_{i \in \,{I_ + }} {Q_i^2} }\\{{n_ - } = \frac{1}{2}\sum\limits_{i \in \,{I_ - }} {Q_i^2} }\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-8076e156019a494fb95eae180cfe712c_l3.png)
we can conclude that the number of solutions to WI-E is
![]()
yielding the total Witten index
with
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{s_i} \equiv \Theta \left( {{n_i}F\left( {{\sigma _{{Q_i}}}} \right)} \right)}\\{\Theta (x) = \left\{ {\begin{array}{*{20}{c}}{1{\rm{ : }}x > 0}\\{0{\rm{ : }}x < 0}\end{array}} \right.}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-65716a3d318765b5152ff1d09809f105_l3.png)
and ![]() implicitly defined by
implicitly defined by
![]()
In subsequent posts, the total Witten index will be used in rather deep ways crossing many fields of mathematics intersecting theoretical physics.