In this post, continuing from part one on Gromov-Witten invariants, I shall derive two deep properties, the second being central about the genus 1 Gromov-Witten potential, and along the way, discuss some propositions regarding the total ancestor potential. Let me introduce the total ancestor potential
where the genus g ancestor potential ![]() is defined by
is defined by
with
![]()
referring to the pull-backs of the classes ![]() , i = 1, …, m, from
, i = 1, …, m, from ![]() relative to the composition
relative to the composition
![]()
Since the sum does not contain the terms with (g, m) = (0, 0),(0, 1),(0, 2) and (1, 0), one can treat ![]() subject to the dilaton shift
subject to the dilaton shift
![]()
as an element in the Fock space depending on the parameter ![]() .
.
Let us implicitly define the operator ![]() on the Laurent 1/z-series completion of the space
on the Laurent 1/z-series completion of the space ![]() defined by
defined by
with the 2-point gravitational descendent in genus 0 being
Now, it is one of the basic facts of quantum cohomology theory that
![]()
that is, given a metaplectic completion of ![]() ,
, ![]() defines a symplectic transformation depending on the parameter
defines a symplectic transformation depending on the parameter ![]() . Put
. Put
![]()
Here is a deep theorem with an excellent proof ‘here’
![]()
For the definition of ![]() , see my last post. Getzler proved the 3g − 2-jet conjecture of Eguchi–Xiong and Dubrovin about genus g descendent potential
, see my last post. Getzler proved the 3g − 2-jet conjecture of Eguchi–Xiong and Dubrovin about genus g descendent potential
![]()
if k1 + … + km > 3g − 3.
Proposition 1
Any quantized symplectic operator of the form
![]()
acts on elements ![]() of the Fock space as
of the Fock space as
with ![]() the power series truncation of
the power series truncation of ![]() with the quadratic form
with the quadratic form
![]()
defined via
Proposition 2
The genus 0 descendent potential equals
which is a deep and famous reconstruction for genus 0 gravitational descendents due to Dubrovin and Dijkgraaf–Witten.
- Let me charter into Frobenius structures. The operator-valued 1-form
![]()
is independent of z and thus defines a linear pencil of connections
![]()
on the tangent bundle ![]() flat for all values of the parameter
flat for all values of the parameter ![]()
hence
![]()
and in coordinate form, ![]() the first condition is equivalent to commutativity
the first condition is equivalent to commutativity
![]()
The correspondence
![]()
defines commutative associative multiplications ![]() on the tangent spaces
on the tangent spaces ![]() , and those are the quantum cup-product, and deeply, we have a coincidence of
, and those are the quantum cup-product, and deeply, we have a coincidence of
![]()
with the third directional derivatives
![]()
of the genus zero Gromov-Witten potential
![Rendered by QuickLaTeX.com \[\bar F_X^0\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e327c237fe1f732840a7af4e393f5ca0_l3.png)
![]()
which explains why ![]() and
and ![]() yielding hence that the quantum cup-product is Frobenius:
yielding hence that the quantum cup-product is Frobenius: ![]() .
.
- A Frobenius structure on a manifold H consists of:
(i) a flat pseudo-Riemannian metric (·, ·),
(ii) a function ![]() whose 3-rd covariant derivatives
whose 3-rd covariant derivatives ![]() are structure constants
are structure constants ![]() of a Frobenius algebra structure: that is, an associative commutative multiplication
of a Frobenius algebra structure: that is, an associative commutative multiplication ![]() satisfying
satisfying
![]()
on the tangent spaces ![]() which depends smoothly on t;
which depends smoothly on t;
(iii) the vector field of unities 1 of the ![]() -product which has to be covariantly constant and preserve the multiplication and the metric.
-product which has to be covariantly constant and preserve the multiplication and the metric.
Now, in Gromov–Witten theory, genus 0 Gromov-Witten invariants of a compact almost Kähler manifold ![]() define on
define on
![]()
a formal structure of a calibrated conformal Frobenius manifold of conformal dimension ![]() , and in the coordinate system
, and in the coordinate system
![]()
corresponding to a graded basis ![]() in
in ![]() , the Euler field takes on the form
, the Euler field takes on the form
![]()
where the constant part ![]() is the 1-st Chern class of the tangent bundle
is the 1-st Chern class of the tangent bundle ![]() .
.
So, proposition 3: The equation ![]() in a neighborhood of a semisimple point
in a neighborhood of a semisimple point ![]() has a fundamental solution in the form
has a fundamental solution in the form
![]()
with
![]()
a formal matrix power series satisfying: ![]()
and the series ![]() satisfying the content of proposition 3 is unique up to right multiplication by diagonal matrices
satisfying the content of proposition 3 is unique up to right multiplication by diagonal matrices ![]() with
with ![]() constants. And, in the case of conformal Frobenius structures the series is uniquely determined by the homogeneity condition
constants. And, in the case of conformal Frobenius structures the series is uniquely determined by the homogeneity condition
![]()
Now, let ![]() be the space of Laurent polynomials in z with coefficients in the tangent space
be the space of Laurent polynomials in z with coefficients in the tangent space ![]() to the Frobenius manifold at a semisimple point
to the Frobenius manifold at a semisimple point ![]() . For
. For ![]() , let
, let
![]()
and let us introduce the direct product
![]()
of N copies of the Witten-Kontsevich tau-function as an element of the Fock space of functions on ![]() . The series
. The series ![]() defines a symplectic transformation on
defines a symplectic transformation on ![]() and set
and set
![]()
and let
![]()
identify the Fock space with its coordinate version, and lastly,
![]()
with ![]() the diagonal entries of the matrix
the diagonal entries of the matrix ![]() in the series
in the series
![]()
which is the 1-form on the Frobenius manifold. Define also the function
![]()
of ![]() defined up to an additive constant.
defined up to an additive constant.
Definition: let the total descendent potential of a semisimple Frobenius manifold be defined by the formula
and introduce the total ancestor potential of a semisimple Frobenius manifold
Property 1 The total descendent potential ![]() of a semisimple Frobenius manifold defined does not depend on the choice of a semisimple point
of a semisimple Frobenius manifold defined does not depend on the choice of a semisimple point ![]() since both
since both
![]()
satisfy the same equation
![]()
with coefficients rational in ![]() . Hence, derivatives of
. Hence, derivatives of ![]() in the directions of the parameter
in the directions of the parameter ![]() vanish as if
vanish as if
![]()
were inverse to each other.
Consequentially, the main property of this post:
Property 2
The genus 1 Gromov-Witten potential 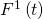 of a semisimple Frobenius manifold is given by the formula
of a semisimple Frobenius manifold is given by the formula
with
![]()
being the inner squares of the canonical idempotents ![]() of the semisimple Frobenius multiplication
of the semisimple Frobenius multiplication ![]() and the genus 1 descendent potential equals
and the genus 1 descendent potential equals
where the partial derivatives are taken with respect to coordinates of ![]() .
.

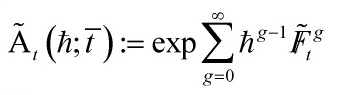
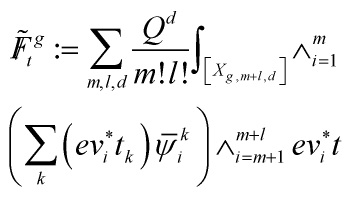
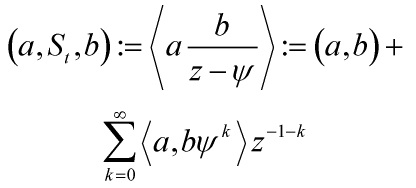
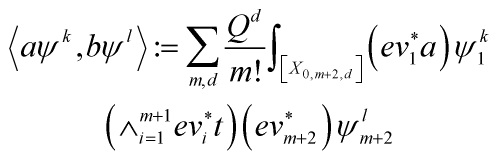
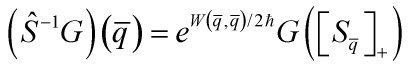
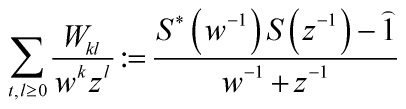
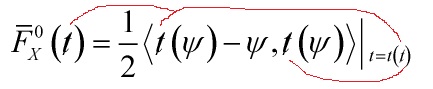
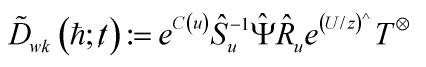
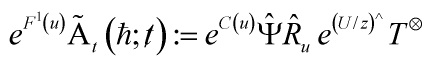
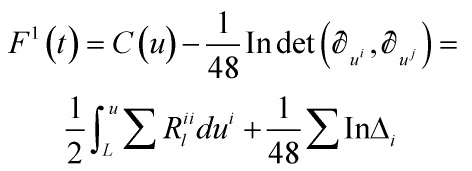
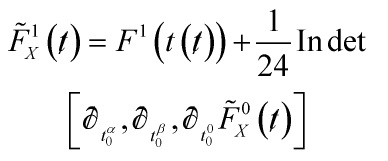


1 Response
Hodge Theory and Gromov-Witten Invariants of Calabi-Yau 3-Folds
Sunday, August 14, 2016[…] discussed Gromov-Witten Invariants and Hodge integrals on numerous occasions. Here, I shall derive three propositions that play a critical role in flux […]