In this post, part one, I will discuss the importance of Gromov-Witten invariants, and for an excellent read, Bernd Siebert’s SGWI is a must. For X a compact almost Kähler manifold of complex dimension D, let ![]() be the moduli orbifold of degree d stable holomorphic maps to X of genus g where d takes values in the lattice
be the moduli orbifold of degree d stable holomorphic maps to X of genus g where d takes values in the lattice ![]() . By compactness,
. By compactness, ![]() is equipped with a rational coefficient virtual fundamental cycle
is equipped with a rational coefficient virtual fundamental cycle ![]() of complex dimension
of complex dimension
and the total descendent potential of ![]() is
is
![]()
with ![]() the genus g descendent potential
the genus g descendent potential
with ![]() being the powers of the 1-st Chern class of the universal cotangent line bundle over
being the powers of the 1-st Chern class of the universal cotangent line bundle over ![]() corresponding to the i-th marked point, and
corresponding to the i-th marked point, and ![]() are pull-backs by the evaluation map
are pull-backs by the evaluation map ![]() at the i-th symplectic-marked point of the cohomology classes
at the i-th symplectic-marked point of the cohomology classes ![]() and
and ![]() is the representative of d in the semigroup ring of the semigroup of degrees of holomorphic curves in X. The genus g Gromov-Witten potential of X is defined as the restriction
is the representative of d in the semigroup ring of the semigroup of degrees of holomorphic curves in X. The genus g Gromov-Witten potential of X is defined as the restriction
![]()
and the genus g descendent potentials are functions on the super-space of vector Laurent polynomials ![]() with coefficients in
with coefficients in ![]() , the cohomology space of X over the Novikov ring.
, the cohomology space of X over the Novikov ring.
According to Witten’s conjecture, which Kontsevich proved, the total descendent potential coincides with the tau-function of the KdV-hierarchy satisfying the string equation
Let the Witten-Kontsevich tau-function be denoted by ![]() and let
and let ![]() be an N-dimensional vector space equipped with a non-degenerate symmetric bilinear form. With
be an N-dimensional vector space equipped with a non-degenerate symmetric bilinear form. With ![]() the space of Laurent polynomials in one indeterminate z with vector coefficients from
the space of Laurent polynomials in one indeterminate z with vector coefficients from ![]() , introduce a symplectic bilinear form in
, introduce a symplectic bilinear form in ![]() by
by
and let ![]() correspond to the decomposition
correspond to the decomposition
![]()
of the Laurent polynomials into polynomial and polar parts, and deeply, note that the subspaces ![]() are Lagrangian. One then quantizes infinitesimal symplectic transformations
are Lagrangian. One then quantizes infinitesimal symplectic transformations ![]() on
on ![]() to order ≤ 2 linear differential operators
to order ≤ 2 linear differential operators ![]() . In a Darboux coordinate system
. In a Darboux coordinate system ![]() compatible with our decomposition
compatible with our decomposition ![]() one has
one has
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{{\left( {{p_\alpha },{p_\beta }} \right)}^ \wedge } = \hbar {{\not \partial }_{{q_\alpha }}}{{\not \partial }_{{q_\beta }}}}\\{{{\left( {{p_\alpha },{p_\beta }} \right)}^ \wedge } = {q_\beta }{{\not \partial }_{{q_\alpha }}}}\\{{{\left( {{p_\alpha },{p_\beta }} \right)}^ \wedge }{q_\alpha }{q_\beta }/\hbar }\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4da3bdd2b2dfd54a7231a16f6f7354eb_l3.png)
with
![]()
holding and ![]() satisfying
satisfying
![]()
and ![]() for any other pairs of quadratic Darboux monomials.
for any other pairs of quadratic Darboux monomials.
Let us move now to the Witten-Kontsevich Tau-function: let
such that
It follows that
which entails
![]()
and thus shows that the operators ![]() are infinitesimal symplectic transformations on
are infinitesimal symplectic transformations on ![]() . However,
. However, ![]() is conjugate to
is conjugate to ![]() , with
, with ![]() , therefore
, therefore ![]() commute as
commute as ![]() and by the Fourier transform, as the vector fields
and by the Fourier transform, as the vector fields ![]() on the line. So, the Poisson brackets satisfy
on the line. So, the Poisson brackets satisfy ![]() and hence we have a representation of the Lie algebra of vector fields on the line to the Lie algebra of quadratic hamiltonians on
and hence we have a representation of the Lie algebra of vector fields on the line to the Lie algebra of quadratic hamiltonians on ![]() .
.
In the 1-dimensional ![]() with the standard inner product, using the Darboux coordinate system
with the standard inner product, using the Darboux coordinate system
on ![]() , one gets
, one gets
We then get
![]()
unless m, n = ±1, in which case:
![]()
Thus the operators ![]() form a representation of the Lie algebra of vector fields on the line.
form a representation of the Lie algebra of vector fields on the line.
So, we get a nice formulation of Kontsevich theorem confirming Witten strikingly bold conjecture. Hence:
Proposition The Witten-Kontsevich tau-function is annihilated by the operators  , m = −1, 0, 1, 2, …; and thus is completely characterized by this property – up to a scalar factor
, m = −1, 0, 1, 2, …; and thus is completely characterized by this property – up to a scalar factor
- Hodge integrals: Let
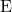 denote the Hodge bundle over the moduli space
denote the Hodge bundle over the moduli space 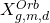 . Then analytically, the fiber of
. Then analytically, the fiber of 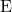 over the point represented by a stable map
over the point represented by a stable map 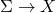 is the complex space of dimension
is the complex space of dimension 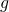 dual to
dual to
![]()
and so ![]() is the pull-back of by the contraction map
is the pull-back of by the contraction map
![]()
of the Hodge bundle over the Deligne-Mumford space. It is a beautiful theorem that even components ![]() of the Chern character vanish. Hence, let us define the total Hodge potential of
of the Chern character vanish. Hence, let us define the total Hodge potential of ![]() as an extension of the total descendent potential depending on the sequence
as an extension of the total descendent potential depending on the sequence ![]() of new variables and incorporating intersection indices with characteristic classes of the Hodge bundles
of new variables and incorporating intersection indices with characteristic classes of the Hodge bundles
which is a family of elements in the Fock space depending on the parameters ![]() ,
,
and here is some depth added to beauty: multiplication by 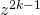 defines an infinitesimal symplectic transformation on
defines an infinitesimal symplectic transformation on 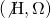 , and letting
, and letting 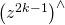 be the corresponding quantization, we get the following
be the corresponding quantization, we get the following
where ![]() are Bernoulli numbers
are Bernoulli numbers
![Rendered by QuickLaTeX.com \[\begin{array}{c}x/\left( {1 - {e^{ - x}}} \right) = 1 + x/2 + \\\sum\limits_{k = 1}^\infty {{B_{2k}}{x^{2k}}} /\left( {2k} \right)!\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1a6a3eeb1859efb75bb8fbc5ffd41f6b_l3.png)

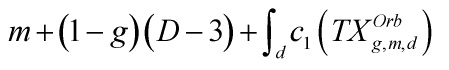

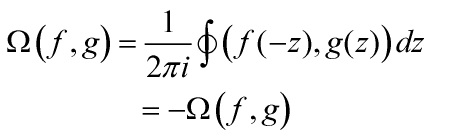
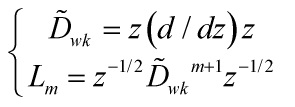

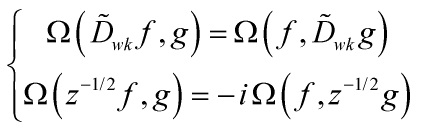
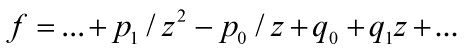
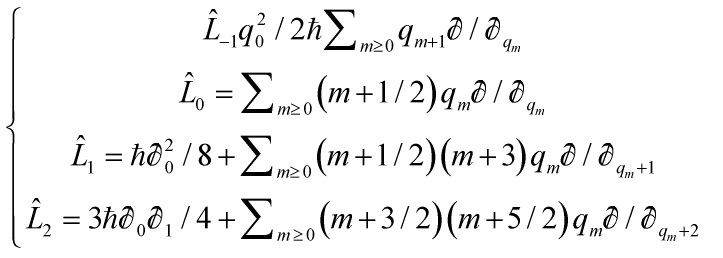
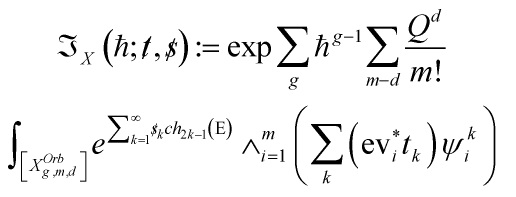
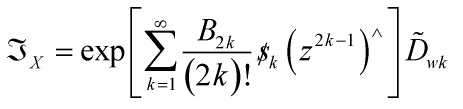


1 Response
Hodge Theory and Gromov-Witten Invariants of Calabi-Yau 3-Folds
Sunday, August 14, 2016[…] discussed Gromov-Witten Invariants and Hodge integrals on numerous occasions. Here, I shall derive three propositions that play a critical role […]