Think of it: of the infinity of real numbers, those that are most important to mathematics — 0, 1, √2, e and π — are located within less than four units on the number line. A remarkable coincidence? A mere detail in the Creator’s grand design? I let the reader decide. ~ Eli Maor, ‘e: The Story of a Number’ (1994)!
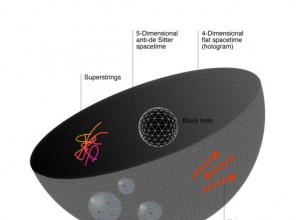
The real, not-so-‘publicized’ magic of M-theory lies in the fact that its Sasaki-Einstein renormalization group is analytically finite. This is part 2 of such mathematical inquisition into the holographic renormalization group in the Maldacena duality D-brane context. One can holographically eliminate space-time, and hence, by GR, 4-dimensional gravity, via entropic cohomological bundle analysis on the Sasaki-Einstein space ![]() and its De Rahm group. One then shaves, via Occam’s razor and the explanatory completeness and causal closure of quantum field theory, all of space-time and gravity. One needs first to do some holographic renormalization group analysis of the Sasaki-Einstein D-p-brane world-volume. Let
and its De Rahm group. One then shaves, via Occam’s razor and the explanatory completeness and causal closure of quantum field theory, all of space-time and gravity. One needs first to do some holographic renormalization group analysis of the Sasaki-Einstein D-p-brane world-volume. Let ![]() be the Calabi-Yau 2-D conic string variable and:
be the Calabi-Yau 2-D conic string variable and:
![]()
with ![]() being the D-p-brane’s p+1 dimensional worldspace Newtonian constant, with
being the D-p-brane’s p+1 dimensional worldspace Newtonian constant, with ![]() the Dirichlet data:
the Dirichlet data:
![]()
with:
![]()
I then deduced the renormalized Hamiltonian action:
![]()
with:
![]()
with ![]() the Gaussian curvature of the Gibbons-Hawkins boundary term of the Calabi-Yau conic tip of
the Gaussian curvature of the Gibbons-Hawkins boundary term of the Calabi-Yau conic tip of ![]() and
and ![]() being the entropic interior of the
being the entropic interior of the ![]() d+1 Riemannian conformally compact manifold
d+1 Riemannian conformally compact manifold ![]() , and
, and ![]() its boundary. Hence, one gets, on
its boundary. Hence, one gets, on ![]() :
:
![]()
with ![]() the matter field Lagrangian density and
the matter field Lagrangian density and ![]() transforms as:
transforms as:
![]()
with ![]() the stress-energy tensor and:
the stress-energy tensor and:
![]()
the renormalization functional of the total holographic renormalization group. Now, let ![]() be the Einstein-Hilbert actional wavefuntion of the universe coupled with the instanton, which is a field configuration that is concentrated at a point in time in the worldvolume of the Dirichlet brane of the corresponding string variable, defined on the Hilbert space corresponding to
be the Einstein-Hilbert actional wavefuntion of the universe coupled with the instanton, which is a field configuration that is concentrated at a point in time in the worldvolume of the Dirichlet brane of the corresponding string variable, defined on the Hilbert space corresponding to ![]() . Let
. Let ![]() denote its Fourier transform. Now, look at the Hodge equation:
denote its Fourier transform. Now, look at the Hodge equation:
![]()
with ![]() the wavefunction of the universe at t = i, and
the wavefunction of the universe at t = i, and ![]() its Fourier transform. Since:
its Fourier transform. Since:
![Rendered by QuickLaTeX.com \[{\Psi ^{wf}}_{U\left| {_{ti}} \right.} = \int\limits_{ - \infty }^\infty {^F{\Psi ^{wf}}_{U\left| {_{ti}} \right.}} (\xi ){e^{2\pi i\xi t}}d\xi \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-8d949d5a0a209a5b38177c4ead91fede_l3.png)
with ![]() the quantum fluctuational frequency of the string worldsheet, we get the required metric that gauges the graviton and its supersymmetric partner:
the quantum fluctuational frequency of the string worldsheet, we get the required metric that gauges the graviton and its supersymmetric partner:
![]()
with:
![]()
which preserves Poincaré invariance and:
![]()
where ![]() is the parametrization function of the interpolating region between branes on the Calabi-Yau conic tip of
is the parametrization function of the interpolating region between branes on the Calabi-Yau conic tip of ![]() , and hence, the supergravity action can now be derived as:
, and hence, the supergravity action can now be derived as:
![]()
with ![]() the
the ![]() metastable false vacuum potential. Now, inserting
metastable false vacuum potential. Now, inserting ![]() in the supergravity action above gives us an energy functional:
in the supergravity action above gives us an energy functional:
![Rendered by QuickLaTeX.com \[{\varepsilon _i} = \frac{1}{{16\pi {G_5}}}\int\limits_{ - \infty }^\infty {d\tau {e^{A(\tau )}}} \left[ {2{{\widetilde \varphi }^2}{ - ^F}{\Psi ^{wf}}_{U\left| {_{INST}} \right.} - 12\widetilde A{{(\tau )}^2} + V(\varphi )} \right]d\,\Omega {({\phi _{si}})^i}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c606a4b89d4b4568ecb7fd68abeda707_l3.png)
and by the Hodge equality, its actional measure is:
![]()
Substituting ![]() in
in ![]() , we get:
, we get:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{\varepsilon _i} = \frac{1}{{16\pi {G_5}}}\int\limits_{ - \infty }^\infty {d\tau {e^{A(\tau )}}} \left\{ {2{{\widetilde \varphi }^2}d{\,^F}{\Psi ^{wf}}_{U\left| {_{INST}} \right.} - 12{{\widetilde A}^2} + \frac{4}{{l_i^2}}{{\left( {\frac{{\not \partial W}}{{\not \partial \varphi }}} \right)}^2} - \frac{{16}}{{3l_i^2}}{W^2}} \right\} = \\\frac{1}{{16\pi {G_5}}}\int\limits_{ - \infty }^\infty {d\tau {e^{A(\tau )}}} \left\{ {2\left( {\widetilde \varphi \pm d{\Psi ^{wf}}_{U\left| {_{INST}} \right.} \mp \frac{{4\not \partial W}}{{l_i^2\not \partial {\varphi _{ij}}}}} \right) - 12{{\left( {\widetilde A(\tau ) \pm \frac{2}{{3{l_i}}}W} \right)}^2} \mp \frac{4}{{{l_i}}}\widetilde \varphi \frac{{\not \partial W}}{{\not \partial {\varphi _{ij}}}} \pm \frac{{16}}{{{l_i}}}A(\tau )W} \right\}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-0ac7154dfcc2cb8b8a0133c14ee90616_l3.png)
Hence, holographic renormalization analytically is achieved for 2 reasons – one: the integral ![]() ranges over all ‘times’, and thus
ranges over all ‘times’, and thus ![]() does satisfy the Wheeler-DeWitt equation, and since it topologically ‘lives‘ on the folliated bundle of
does satisfy the Wheeler-DeWitt equation, and since it topologically ‘lives‘ on the folliated bundle of ![]() , by holographic elimination, it is a wavefunction describing, vacuously, quantum gravity, and, secondly: its solution describes ‘finite’ renormalization Clifford algebraic variables, and so we have exact-off-hand renormalization. Hence, we can derive the initial singularity ‘creation’ relation in a finite way describing a holographic elimination of space-time, and hence, by GR, gravity, via squaring:
, by holographic elimination, it is a wavefunction describing, vacuously, quantum gravity, and, secondly: its solution describes ‘finite’ renormalization Clifford algebraic variables, and so we have exact-off-hand renormalization. Hence, we can derive the initial singularity ‘creation’ relation in a finite way describing a holographic elimination of space-time, and hence, by GR, gravity, via squaring:
![Rendered by QuickLaTeX.com \[\frac{d}{{dt}}\left( {\underbrace {\int_0^{\delta {f_K}} {\frac{{\frac{d}{{d{t^ \circ }}}{\Psi ^{wf}}_{U\left| {_{INST}} \right.}(eh)}}{{\alpha ({t^ \circ })}}} }_{Creation}\,\, + \underbrace {\int_{{\delta _f}}^{{f_K}} {\frac{{\frac{d}{{d{t^ \circ }}}{\Psi ^{wf}}_{U\left| {_{INST}} \right.}{{(eh)}^{2\pi i\xi t}}}}{{\alpha ({t^ \circ })}}} }_{QuantumGravity}} \right)d\,\Omega {({\phi _{si}})^2}dt\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-437bf0f7e722eb05a198b0083a9075fa_l3.png)
One can hence deduce that space-time and gravity are holographic entropic projections of the Fukaya category of the Sasaki-Einstein AdS/CFT space. To be continued.
THE ART OF DOING MATHEMATICS CONSISTS IN FINDING THAT SPECIAL CASE WHICH CONTAINS ALL THE GERMS OF GENERALITY. ~ DAVID HILBERT!