The Theory of Everything, if you dare be bold, might be something more than a string orbifold. While some of your leaders have got old and sclerotic, not to be trusted alone with things heterotic, please heed our advice that you are not smitten – the Book is not finished, the last word is not ‘WITTEN’. ~ Sheldon L. Glashow (On Edward Witten)!
In this post, I urge you to keep your eyes on the numbers as they qualify the type of branes and worldvolumes, as well as worldspaces as derived category of coherent sheaves in Calabi–Yau settings. By now, the centrality of D3-branes should be clear for Grand Unification Physics from my last three posts in the sense that their existence is a necessary condition for the integrability of the supergravity action, and in the 2nd-quantized context, as I showed, one must work with the Gaillard-Zumino Condition: that is, essentially using 8-loop counterterms with superspace torsion
with being the superfield torsion, and by the GKP-Witten Relation, derived the Lagrangian action for D3-branes
with
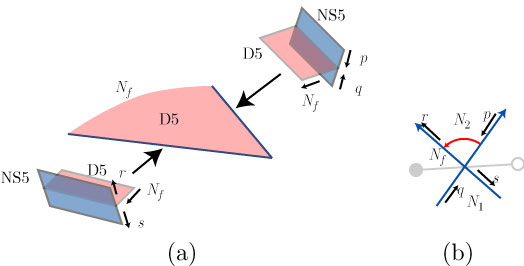
One must however do Hamiltonian analysis due to the fact that its corresponding Hilbert operator encodes the total energy information of physical systems and its Fock spectrum is the complete set of measurement outcomes with respect to energy, as well as due to the fact that it is analytically connected to the Klein-Fock-Gordon equation. But the D3-brane Hamiltonian analysis can only be carried in a BPS bounded energy of a D5-brane in the background geometry of the D3-brane’s 4-dimensional worldvolume: WHY D5-branes is the obvious question – because the D5-brane’s worldvolume is 6 dimensional, 4 to embed the 4-dimensions of the D3-brane’s 4-dimesional worldvolume, and the extra 2 to embed the compactification spaces corresponding to the open and closed strings. Really, numbers are everything and mathematics is magic! If you keep track of the ‘numbers‘, this post should make you a Pythagorean. So let us march on:
The 10-dimensional metric is given by
with being Cartesian coordinates for
and
being the line bundle on the unit 5-sphere parametrized by the angular coordinates
,
,
, with
the coordinates of the 4-sphere self-dual topological pull-back. And so, we get
and the harmonic function is given by
where describes the horizon geometry of
and describes an asymptotic flat spacetime.
is a parametric measure of the gravitational ‘size’ of the brane stack: with
, it is identical to the radius of
and
. Moreover, the supergravitational description of the D3-brane action are uniquely characterized by a non-vanishing RR-5-form field
with
and generally, is the volume n-form on a unit n-sphere, and
. Now, the action of a D5-brane coupled to a D3-brane background with the above information, is
where is the D5-brane worldspace, and the RR-5-form field embeds the D3-brane worldvolume gauge field
via a Wess-Zumino coupling given by
above. One gets to the Hamiltonian formalism in order to deduce the total Schrödinger energy bound on the spacetime topology. The gauge coordinates on the D5-brane worldvolume are maximally informative by picking
and setting
and by an symmetry preservation that have
invariants, one must work with the following conditions
with all this in place, we get the D5-brane action
with
and is the volume of the unit 4-sphere. It then follows that the momenta
and
conjugate to
and
and so they are given by
and the Fock space Lagrangian density is by definition
and by inversion, the Hamiltonian form of
is
with . The first term of the energy density is
and the second term gives us the supersymmetric Gauss Law
which one solves via
where is the outer measure of integration on
. Thus, the BPS condition implies the reduction
where
and given as
Note now that the key integral
is essentially topological, which implies analytically that the required BPS bound on the D5-brane energy is
with being the vacuum energy of the D5-brane in the D3-brane background, and
is the renormalization group representation factor. The BPS condition in
has 2nd-quantized saturation in the Fock space if and only if both inequalities hold true on the boundary. Hence, the sign of
is completely determined by the sign of
where
and is monotonically increasing for
Now, the topological nature of can be redefined as a total derivative
which implies that
and hence is invariant under supersymmetric group action as well as under Poincaré group variation of the gauge fields: for
,
is exactly the ground vacuum state energy of the D5-worldvolume under quantum fluctuation of its worldspace
with its corresponding 5-dimensional hypersphere in the transverse space to the D4-worldvolume of the D3-brane, which one must interpret, by D3-brane self-duality and Poincaré invariance, as a
hyperplane: so the energy is
For ,
vanishes completely, and so the PHILOSOPHICAL IMPORT is that quantum fluctuations of the D5-worldspace
in the horizon geometry of the D3-brane are the limit of the D5 quantum vacua of the D4-worldvolume of the D3-brane. Moreover, and deeper still, the D5-brane worldspace
under quantum fluctuation of its 6-dimensional worldvolume represents a D5-brane infinitely far from the D3-brane BUT are in super-Yukawa quantum entanglement via
6-stack strings, and so when
, as it must by unitarity, we get the deep scientific and philosophical ‘generality’: D5-brane worldspaces
represent a quantization of 4D-worldvolumes of D3-branes with BPS ground vacua states at infinity, and
living on the tori-throat of
. Thus, in the strict topological Wess–Zumino limit, the D5 background disappears! Further evidence that quantum gravity and thus spacetime are holographic entropic emergent properties of the gauge bundle of
with BPS constraints. Having derived and
, the Grand Unification Program takes us next to an analysis of self-duality in the M-theoretic context of super-D3-branes and their actions.
INDEED!