Where is the real? All appearance are deceitful, the visible surface is deceptive. I look at my hand.. ..It is nerves, muscles, bones. Let us go deeper: it is molecules and acids. Further still: it is an impalpable waltz of electrons and neutrons. Further still: an immaterial nebula. Who can prove that my hand exists? ~ Salvador Dalí!
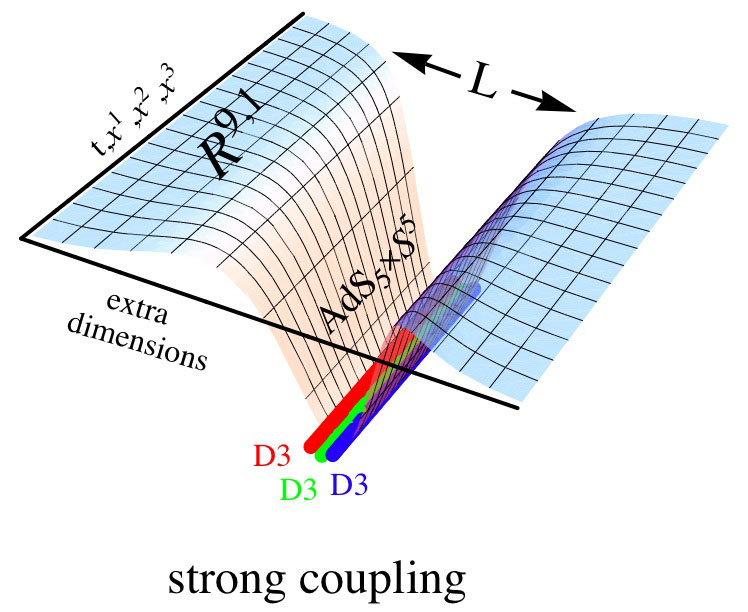
In my last post, I introduced the notions of a p-brane and D-brane (D for Dirichlet) and provided some of the most essential facts about them, and went on to show that the ONLY solutions to the D = 10/D = 11 supergravity actions ARE p-branes, and D-branes in the ![]() setting. In this post, I will show why, for p = 3, D3-branes are highly unique and critical in unification physics. First, the propagation of a D3-brane through spacetime generates a 4-dimensional worldvolume
setting. In this post, I will show why, for p = 3, D3-branes are highly unique and critical in unification physics. First, the propagation of a D3-brane through spacetime generates a 4-dimensional worldvolume ![]() that has 4-dimensional Poincaré invariance: this is crucial since the generators of the Poincaré group and the generators of the Supersymmetry group are in convolution, and that analytically implies that superstring theory is a quantum theory of gravity and hence of spacetime, and thus Supergravity can be derived by solving
that has 4-dimensional Poincaré invariance: this is crucial since the generators of the Poincaré group and the generators of the Supersymmetry group are in convolution, and that analytically implies that superstring theory is a quantum theory of gravity and hence of spacetime, and thus Supergravity can be derived by solving
![]()
with
![]()
![]()
![]()
and ![]() being the 4-dimensional Minkowski metric. Note that we have
being the 4-dimensional Minkowski metric. Note that we have ![]() . The Second criticality regarding D3-branes is that the open string worldsheet generating the graviton via quantum fluctuations can be topologically embedded in
. The Second criticality regarding D3-branes is that the open string worldsheet generating the graviton via quantum fluctuations can be topologically embedded in ![]() space via the irreducible representation of its De Rham cohomology group by use of Stokes’ theorem. The Third point is that D3-branes have constant axion and dilaton fields, which are necessary conditions by gauge and unitarity constraints. A fourth criticality is that a D3-brane is self-dual. The solution can be characterized by
space via the irreducible representation of its De Rham cohomology group by use of Stokes’ theorem. The Third point is that D3-branes have constant axion and dilaton fields, which are necessary conditions by gauge and unitarity constraints. A fourth criticality is that a D3-brane is self-dual. The solution can be characterized by ![]() ,
, ![]() constant,
constant, ![]() ,
,
![]()
![]()
where ![]() is the volume of the transverse to the 4-D Minkowskian D3-brane in D = 10/D = 11 supergravity theory. So, a D3-brane solution is a 2-parameter family of solutions indexed by the string coupling constant
is the volume of the transverse to the 4-D Minkowskian D3-brane in D = 10/D = 11 supergravity theory. So, a D3-brane solution is a 2-parameter family of solutions indexed by the string coupling constant ![]() and the instanton angle
and the instanton angle ![]() , with modular parameter
, with modular parameter
![]()
By the self-duality of D3-branes, we hence have a string-gauge correspondence
![]()
in ![]() space, and so the gravitonic D3-brane action is
space, and so the gravitonic D3-brane action is
![]()
Now here is where the Poincaré symmetry comes in: in the crucial case of N = 1 sypersymmetry, its irreducible representation allows us to identify the massless fermions with the Goldstinos. One finds that the field ![]() and the gauge fields
and the gauge fields ![]() are
are ![]() times the normalized fields in canonical form: so, Eq. 2. reduces to
times the normalized fields in canonical form: so, Eq. 2. reduces to
![]()
with
![]()
and ![]() . Note now that
. Note now that ![]() , with
, with ![]() being the radius of
being the radius of ![]() and
and ![]() is the D3-brane tension. So, it follows that
is the D3-brane tension. So, it follows that ![]() , with
, with ![]() being the number of c-brane stacks on the conformal boundary. But, it is not apriori of the same order of magnitude as the Planck length
being the number of c-brane stacks on the conformal boundary. But, it is not apriori of the same order of magnitude as the Planck length ![]() , however, their ratio is given by
, however, their ratio is given by
![]()
This identity is crucial for the Lagrangian, where in D = 10, becomes
![]()
and by a supersymmetric transformation induced by ![]() , we get
, we get
![]()
and
![]()
for a Majorana-Weyl spinor gaugino ![]() and the Lagrangian density can be derived now as
and the Lagrangian density can be derived now as
![Rendered by QuickLaTeX.com \[\begin{array}{c}6.\quad L = \frac{1}{{{\gamma _A}^2}}{\phi ^4}\left( {1 - \sqrt {\left( {1 + \frac{{\gamma _A^2\left[ {{\phi ^ + } - {E^2}} \right]}}{{{\phi ^4}}}} \right)\left( {1 + \frac{{\gamma _A^2{B^2}}}{{{\phi ^4}}}} \right)} } \right)\\ + {g_s}\chi {G_{\tau \tau }}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bdcaf6947cea9fd321d7120ea83b99b2_l3.png)
with
![]()
where the field conjugate to ![]() is
is
![Rendered by QuickLaTeX.com \[\begin{array}{c}8.\quad \not D = \frac{{\partial L}}{{\partial {G_{\tau \tau }}}} = {G_{\tau \tau }}\sqrt {\frac{{1 + \gamma _A^2{F_{\mu \nu }}/{\phi ^4}}}{{1 + \gamma _A^2\left[ {{{\left( {{\phi ^\dagger }} \right)}^2} - G_{\tau \tau }^ + } \right]}}} \\ + \,{g_s}\chi {G_{\tau \tau }}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-8dd310892e57c02c243bd0d827ebaacf_l3.png)
Now the GKP-Witten relation for D3-branes
![]()
gives us canonically
![Rendered by QuickLaTeX.com \[9.\quad {Z_{CFT}}{\left[ {\frac{{\mathop {{\rm{lim}}}\limits_{{\sigma _t} \to \infty } {\rm{propagation}}\,{\rm{(}}WV_P^{D3}{{({\sigma _t})}^{R{{_{{S_{({\sigma _s},{\sigma _t})}}}^{2d}}_{{\sigma _s} \to 0}}}}}}{{{\rm{boundary}}\,{\rm{(}}WV_P^{D3})}}J_\omega ^{\nabla - 3 + \tau } = J_{D3}^{{\rm{current}}}} \right]_{D3 - brane}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-52b137875cae08d015c167b9da6c1dee_l3.png)
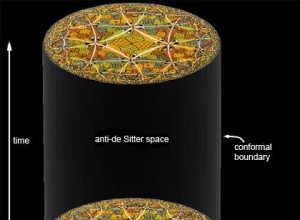
thus entailing that spacetime ‘lives’ on the boundary of ![]() and ‘time‘ and ‘space‘ as Hilbert space functors are interpretable as holomorphic emergent entropic properties of the integrable forms of the exterior algebra of the D3-brane 4-dimensional worldvolume
and ‘time‘ and ‘space‘ as Hilbert space functors are interpretable as holomorphic emergent entropic properties of the integrable forms of the exterior algebra of the D3-brane 4-dimensional worldvolume ![]() dynamically propagating in time as
dynamically propagating in time as ![]() .
.
Now, we need to see how the quantization can be carried out for the D3-brane: with ![]() the Planck length for D3-branes’ 4-dimensional worldvolume
the Planck length for D3-branes’ 4-dimensional worldvolume ![]() , we get
, we get
![]()
with ![]() being the D3-brane tension, where, explicitly
being the D3-brane tension, where, explicitly
![]()
with
![]()
is the D = 10 gravitational constant. Now: in the all-too important ![]() setting, there is a gauge operator
setting, there is a gauge operator ![]() ‘living‘ on the boundary of
‘living‘ on the boundary of ![]() with non-trivial quantum fluctuation of its self-dual supergravity field
with non-trivial quantum fluctuation of its self-dual supergravity field ![]() propagating in the bulk of
propagating in the bulk of ![]() , and hence we get
, and hence we get
![]()
with boundary conditions for the supergravity field ![]()
![]()
with ![]() being the conformal dimension of the operator
being the conformal dimension of the operator ![]() . The central argument of this post now is clear: by Eq. 9, the ONLY way one can derive a finite quantum theory of gravity, and by GR, spacetime, satisfying gauge and unitarity constraints, is if the action of that theory is ONLY integrable, and it is, on a 5-dimensional Sasaki-Einstein Manifold
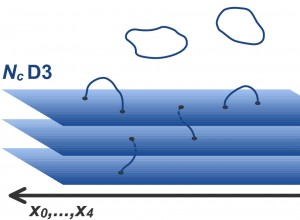
. The central argument of this post now is clear: by Eq. 9, the ONLY way one can derive a finite quantum theory of gravity, and by GR, spacetime, satisfying gauge and unitarity constraints, is if the action of that theory is ONLY integrable, and it is, on a 5-dimensional Sasaki-Einstein Manifold ![]() that has a ‘D3-brane’ 4-dimensional worldvolume
that has a ‘D3-brane’ 4-dimensional worldvolume ![]() homological reduction that places its corresponding stack
homological reduction that places its corresponding stack ![]() D3-branes at the ‘tip’ of a Calabi–Yau manifold corresponding to the string-compactification, with the cone topologically embedded in
D3-branes at the ‘tip’ of a Calabi–Yau manifold corresponding to the string-compactification, with the cone topologically embedded in ![]() . This is as deep as mathematical results ‘get’ in physics, or any science for that matter. I shall next start explicitly quantizing the action(s) of D3-branes.
. This is as deep as mathematical results ‘get’ in physics, or any science for that matter. I shall next start explicitly quantizing the action(s) of D3-branes.