Eleven-dimensional supermembrane theory is apriori related to M-theory since string-string duality entails an equivalence between the membrane action corresponding to ![]() and the
and the ![]() orbifold action of
orbifold action of ![]() . Also, D3-branes in a D3/D7-brane system in F-theory naturally correspond to M5-branes in M-theory compactified on a Type-II-A/B torus in light of the M-F theory duality, and instantons that arise from D3-branes wrapping internal divisors on a Calabi-Yau 3-fold correspond to M5-brane instantons in M-theory compactified on an elliptically fibered Calabi-Yau 4-fold. Furthermore, M5-branes wrapped on multi-centred Taub-NUT spaces, of which paradigmatic instances are ALF hyper-Kähler four-manifolds, locally asymptotic at infinity to
. Also, D3-branes in a D3/D7-brane system in F-theory naturally correspond to M5-branes in M-theory compactified on a Type-II-A/B torus in light of the M-F theory duality, and instantons that arise from D3-branes wrapping internal divisors on a Calabi-Yau 3-fold correspond to M5-brane instantons in M-theory compactified on an elliptically fibered Calabi-Yau 4-fold. Furthermore, M5-branes wrapped on multi-centred Taub-NUT spaces, of which paradigmatic instances are ALF hyper-Kähler four-manifolds, locally asymptotic at infinity to , are central to deriving the Standard Model of physics from F-theory via ADE elliptic fibrational Tate-Hitchin brane-webs in light of the M-F theory duality. This underlies the main theoretical reason why string/M-theory is the only quantum theory of gravity that incorporates gauge theories, chiral matter, and spontaneously broken symmetries. The self-duality of the D3-brane and the string-string duality suggest a pure spinor action as the basis of the Euler-Lagrange EOM. Here I shall discuss some relations to Hořava–Witten theory, the Hitchin equation, and Tate’s algorithm. Let us recall that the bosonic sector membrane action is given by:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{S = {S_M} + \int_{\partial {M^3}} {\left\{ {\frac{1}{2}} \right.} \left( {{g_{mn}}{\eta ^{ij}} + {b_{mn}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^m}{\partial _j}{x^n} + \frac{1}{2}\left( {{g_{IJ}}{\eta ^{ij}} + {b_{IJ}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^I}{\partial _j}{x^J} + {\varepsilon ^{ij}}{\partial _i}{x^J}{\partial _j}{x^m}\left. {A_m^J(x)} \right\}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4882eceed14877eb1333bb4a24c24503_l3.png)
where:
![]()
Also, recall that the total action is given as such:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S^{T}} = \frac{1}{{2\pi {\alpha ^\dagger }12}}\int\limits_{{\rm{world - volumes}}} {{d^{26}}} x\,d\,\Omega {\left( {{\phi _{inst}}} \right)^2}\sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} \,{e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}} \cdot \\\left( {{R_{icci}} - 4{{\left( {{{\not D}^{susy}}\left( {{\phi _{inst}}} \right)} \right)}^2}} \right) + \frac{1}{{12}}H_{3,\mu \nu \lambda }^bH_3^{b,\mu \nu \lambda }/A_\mu ^H + \sum\limits_{D - p - branes} {S_{Dp}^{WV}} \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-452301a9de070e4bc6e9d7128ca1ad99_l3.png)
which is highly non-trivial since Clifford algebras are metaplectic quantizations of exterior algebras. Applying piece-wise to the Poincaré line bundle, we get by Gaussian matrix elimination, an expansion of ![]() via Green’s function, yielding the on-shell action of M-theory in the Witten gauge:
via Green’s function, yielding the on-shell action of M-theory in the Witten gauge:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_M} = \frac{1}{{{k^9}}}\int\limits_{{\rm{world - volumes}}} {{d^{11}}} \sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} {T_p}^{10}d\Omega {\left( {{\phi _{inst}}} \right)^{26}}\left( {{R_{icci}} - A_\mu ^H\frac{1}{{48}}G_4^2} \right) + \\\sum\limits_{Dp} {D_\mu ^{susy}} {e^{ - H_3^b}}/S_{Dp}^{WV} + \sum\limits_{Dp} {D_\nu ^{susy}} {e^{H_3^b}}/S_{Dp}^{SV}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1a0ae0e886994172b2227819ca6950f2_l3.png)
with Kähler-Yang-Mills-Dirac form:
![]()
where:
![]()
with:
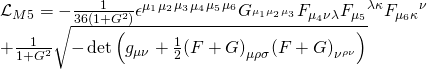
with ![]() the kappa symmetry term,
the kappa symmetry term, ![]() the metric on
the metric on ![]() , and
, and ![]() the corresponding coordinates with
the corresponding coordinates with ![]() an antisymmetric 3-tensor. Hence, the worldvolume
an antisymmetric 3-tensor. Hence, the worldvolume ![]() is:
is:
![]()
and where the Hamiltonian metaplectic action in the Heisenberg representation on the Dp+1 dimensional worldspaces gives us:
![]()
where:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{\Im _i} = - \not \partial {\phi _{si}}{T_{Dp}}d\,\Omega {{({\phi _{si}})}^{2\pi ik}}}\\{\not K = - {{\not \partial }_i}{{\widetilde E}^i} + {{( - 1)}^{p + 1}}{T_{Dp}}{S^{{\rm{Fer}}}}}\\{{{\not H}_i} = \widetilde P{\alpha _i}\widetilde E_i^\alpha {{\not \partial }_i}{\phi _{si}} + \widetilde E{{\not F}_{ij}}}\\{H = \frac{1}{{2\pi ik}}\left[ {{{\widetilde P}^2} + {{\widetilde E}^i}{{\widetilde E}^j}{G_{ij}} + T_{Dp}^2{e^{ - 2{\phi _{si}}}}{\rm{det}}\left( {{G_{ij}} + {{\not F}_{ij}}} \right)} \right]}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bd828556ea51b8c78862eb753658693f_l3.png)
with:
![]()
and:
![]()
The bosonic sector hence lives on the boundary of the open membrane. Two copies of ![]() naturally couple to the U(1) connections
naturally couple to the U(1) connections ![]() .
.
The bosonic part of our action is then given by:
![]()
with the 11D SUGRA part:
![]()
and the Yang-Mills part:
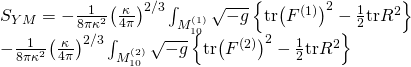
with sources given by:
![]()
Now, double dimensional reduction of the twisted supermembrane on:
![]()
of
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{S = {S_M} + \int_{\partial {M^3}} {\left\{ {\frac{1}{2}} \right.} \left( {{g_{mn}}{\eta ^{ij}} + {b_{mn}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^m}{\partial _j}{x^n} + \frac{1}{2}\left( {{g_{IJ}}{\eta ^{ij}} + {b_{IJ}}{\varepsilon ^{ij}}} \right)}\\{{\partial _i}{x^I}{\partial _j}{x^J} + {\varepsilon ^{ij}}{\partial _i}{x^J}{\partial _j}{x^m}\left. {A_m^J(x)} \right\}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4882eceed14877eb1333bb4a24c24503_l3.png)
entails that the bosonic sector is that of the heterotic string:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{{S_h}\int {{d^2}} \sigma \left\{ {\frac{1}{2}} \right.\left( {{g_{mn}}{\eta ^{ij}} + {b_{mn}}{\varepsilon ^{ij}}} \right){\partial _i}{x^m}{\partial _j}{x^n}}\\{ + \frac{1}{2}\left( {{g_{IJ}}{\eta ^{ij}} + {b_{IJ}}{\varepsilon ^{ij}}} \right){\partial _i}{x^I}{\partial _j}{x^I} + }\\{{\varepsilon ^{ij}}{\partial _i}{x^I}{\partial _n}{x^m}\left. {A_m^{(I)}(x)} \right\}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d29fbffef61d22da311051a09bec0ceb_l3.png)
with gauge group indices I = 1, … , 16, where general Dp-brane solutions, p = 1, 2, 3, 4 preserving 1/2 SUSY, are of the general form:
![]()
![]()
![]()
![]()
and where the M5-brane action in a D = 11 SUGRA background is given by:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}S=2\int_{{{{M}_{6}}}}{{d{{x}^{6}}}}\left[ {\sqrt{{-\det \left( {{{g}_{{\mu \nu }}}+i{{{\tilde{H}}}_{{\mu \nu }}}} \right)}}} \right.\\+\frac{{\sqrt{{-g}}}}{{4{{{\left( {\partial a} \right)}}^{2}}}}{{\partial }_{\lambda }}a{{{\tilde{H}}}^{{\lambda \mu \nu }}}\left. {{{H}_{{\mu \nu \rho }}}{{\partial }^{\rho }}_{a}} \right]-\int_{{{{M}_{6}}}}{{{{C}_{6}}}}+{{H}_{3}}\wedge {{C}_{3}}\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f2a7df4d5552e0c092ce01b23b22cfbe_l3.png)
with:
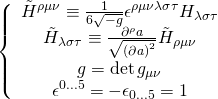
and the ![]()
![]() Lagrangian is:
Lagrangian is:
![]()
with covariant derivative given by:
![]()
and the Chern-Simons term is:
![]()
Now consider:
![]()
with:
![]()
Since the worldsheet action:
![]()
is now just a sum of three terms:
![]()
![]()
![]()
and the index I = 1, … , 22 labels 22 gauge fields, 16 coming from the internal dimensions of the heterotic string, and the other 6 gauge fields are the KK modes of the metric and antisymmetric tensor, the action ![]() then has a massless spectrum given by moduli fields corresponding to deformations of the Narain lattice and thus take values in the group manifold:
then has a massless spectrum given by moduli fields corresponding to deformations of the Narain lattice and thus take values in the group manifold:
![]()
Hence, the gauge fields are defined in terms of superfields living on 10-dimensional boundaries of M-solutions with natural interpretation as the product-spaces of multi-centered Taub-NUT solutions and elliptically fibered Calabi-Yau 4-folds modded by the orbifold action of Type-II-B ![]() Hitchin fibrations.
Hitchin fibrations.
The 11d kappa-symmetric SM action has two parts:
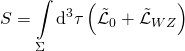
with:
![]()
and:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{{\tilde{\mathcal{L}}}}_{{WZ}}}={{\epsilon }^{{ijk}}}\left[ {\frac{1}{6}{{{\tilde{\mathcal{H}}}}_{{\mu \nu \rho }}}{{\partial }_{i}}{{x}^{\mu }}{{\partial }_{j}}{{x}^{\nu }}{{\partial }_{k}}{{x}^{\rho }}-\frac{i}{4}} \right.\left\{ {\bar{\theta }\,{{\Gamma }_{{\mu \nu }}}} \right.{{\partial }_{i}}\theta \,{{\partial }_{j}}{{x}^{\mu }}{{\partial }_{k}}{{x}^{\nu }}\\+\frac{i}{2}\bar{\theta }\,{{\Gamma }_{{\mu \nu }}}{{\partial }_{i}}\theta \bar{\theta }\,{{\Gamma }^{\mu }}{{\partial }_{i}}\theta \,{{\partial }_{k}}{{x}^{\nu }}-\frac{1}{{12}}\bar{\theta }\,{{\Gamma }_{{\mu \nu }}}{{\partial }_{i}}\theta \bar{\theta }\,{{\Gamma }^{\mu }}\left. {{{\partial }_{j}}\theta \bar{\theta }\,{{\Gamma }^{\nu }}\left. {{{\partial }_{k}}\theta } \right\}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-90950f5ecc8a01a979b8d236c2b958cb_l3.png)
and where we have defined:
![]()
and we have:
![]()
and where:
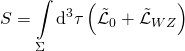
is kappa-symmetric and supersymmetric and the kappa-symmetric pure spinor action is given by a BRST-symmetric functional:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{S}_{{PS}}}=\int\limits_{\Sigma }{{{{\text{d}}^{3}}}}\tau \left[ {{{{\tilde{P}}}_{\mu }}\Pi _{0}^{\mu }+{{{\tilde{\mathcal{L}}}}_{{WZ}}}+{{d}_{\alpha }}{{\partial }_{0}}{{\theta }^{\alpha }}} \right.+{{w}_{\alpha }}{{\partial }_{0}}{{\lambda }^{\alpha }}+\left( {d{{\Gamma }_{\mu }}{{\partial }_{I}}\theta } \right)\Pi _{J}^{\mu }{{\epsilon }^{{IJ}}}\\-\frac{1}{2}\left( {{{{\tilde{P}}}^{\mu }}{{{\tilde{P}}}_{\mu }}+\det \left( {{{\Pi }_{I}}{{\Pi }_{J}}} \right)} \right)+{{e}^{I}}\left( {{{{\tilde{P}}}_{\mu }}\Pi _{I}^{\mu }+d{{\partial }_{I}}\theta +w{{\partial }_{I}}\lambda } \right)\\+\left( {w{{\Gamma }_{\mu }}{{\partial }_{I}}\lambda } \right)\Pi _{J}^{\mu }{{\epsilon }^{{IJ}}}-i{{\epsilon }^{{IJ}}}\left( {w{{\Gamma }_{\mu }}{{\partial }_{I}}\theta } \right)\left( {\bar{\lambda }{{\Gamma }^{\mu }}{{\partial }_{J}}\theta } \right)+i{{\epsilon }^{{IJ}}}\left( {w{{\partial }_{I}}\theta } \right)\left. {\left( {\bar{\lambda }\,{{\partial }_{J}}\theta } \right)} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bade2f0c3de3e57465c2296109891b4f_l3.png)
with ![]() a fermionic constraint-operator:
a fermionic constraint-operator:
![]()
And the Hořava–Witten 5D action is given as so:
![]()
![]()
![]()
![]()
and the first Pontrjagin class of our Calabi-Yau is:
![]()
Now note that the SM action ![]() is invariant under the SUSY transformations:
is invariant under the SUSY transformations:
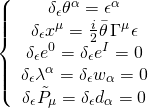
and the BRST operator:
![]()
acts on fields as such:
![]()
with the following holding:
![Rendered by QuickLaTeX.com \displaystyle \left\{ {\begin{array}{*{20}{c}} {\left\{ {{{p}_{\alpha }},{{\theta }^{\beta }}} \right\}=-i\delta _{\alpha }^{\beta }} \\ {\left[ {{{P}_{\mu }},{{x}^{\nu }}} \right]=i\delta _{\mu }^{\nu }} \\ {\left[ {{{\lambda }^{\alpha }},{{w}_{\beta }}} \right]=-i\delta _{\alpha }^{\beta }} \end{array}} \right.](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-33f4eb0ed211839cf835d871b6d3ad1a_l3.png)
Hence, we can derive the following:
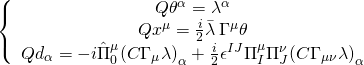
and:
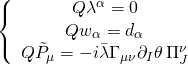
with three pure spinor constraints:
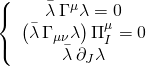
Thus, the PS action ![]() :
:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{S}_{{PS}}}=\int\limits_{\Sigma }{{{{\text{d}}^{3}}}}\tau \left[ {{{{\tilde{P}}}_{\mu }}\Pi _{0}^{\mu }+{{{\tilde{\mathcal{L}}}}_{{WZ}}}+{{d}_{\alpha }}{{\partial }_{0}}{{\theta }^{\alpha }}} \right.+{{w}_{\alpha }}{{\partial }_{0}}{{\lambda }^{\alpha }}+\left( {d{{\Gamma }_{\mu }}{{\partial }_{I}}\theta } \right)\Pi _{J}^{\mu }{{\epsilon }^{{IJ}}}\\-\frac{1}{2}\left( {{{{\tilde{P}}}^{\mu }}{{{\tilde{P}}}_{\mu }}+\det \left( {{{\Pi }_{I}}{{\Pi }_{J}}} \right)} \right)+{{e}^{I}}\left( {{{{\tilde{P}}}_{\mu }}\Pi _{I}^{\mu }+d{{\partial }_{I}}\theta +w{{\partial }_{I}}\lambda } \right)\\+\left( {w{{\Gamma }_{\mu }}{{\partial }_{I}}\lambda } \right)\Pi _{J}^{\mu }{{\epsilon }^{{IJ}}}-i{{\epsilon }^{{IJ}}}\left( {w{{\Gamma }_{\mu }}{{\partial }_{I}}\theta } \right)\left( {\bar{\lambda }{{\Gamma }^{\mu }}{{\partial }_{J}}\theta } \right)+i{{\epsilon }^{{IJ}}}\left( {w{{\partial }_{I}}\theta } \right)\left. {\left( {\bar{\lambda }\,{{\partial }_{J}}\theta } \right)} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bade2f0c3de3e57465c2296109891b4f_l3.png)
is manifestly BRST invariant, since the following holds:
![]()
Consequently, the BRST action has remnant surface terms whose vanishing on D-brane worldvolumes has deep ramifications for Dirichlet-branes of SMs whose 3-form fluxes couple to M2-branes. Note that the remnant surface terms are defined by the following relation:
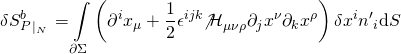
with ![]() constant on the Dp-brane worldvolume, with Neumann boundary condition:
constant on the Dp-brane worldvolume, with Neumann boundary condition:
![]()
and Dirichlet boundary condition:
![]()
The BRST action on ![]() is a pure WZ transformation:
is a pure WZ transformation:
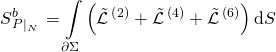
![]()
![]()
![]()
Kappa-symmetry and SUSY entail that the surface terms vanish identically on Dp-brane-worldvolumes, and we have the central flux relation:
![]()
Now, non-commutative M-branes have gluing matrices and 3-form fluxes which entail that fermionic boundary conditions solve:
![]()
In the M5 case, we have:
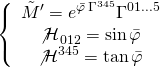
satisfying the self-duality condition on the M5-brane worldvolume. In the zero-case, we have:
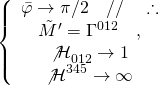
and yields a critical M2-brane ending on a NC M5-brane, and hence a NC M5-brane is a bound state of an M5-brane and M2-branes.
In the case of the NC M9-brane, there are two cases to consider: with E-flux and with M-flux. Consider:
![]()
Then from the gluing condition and kappa-symmetry, we can derive:
![]()
![]()
Hence:
![]()
is satisfied given that:
![]()
holds. In the Dirichlet direction, we have in the 10th dimension, the following relation holding:
![]()
and hence the gluing matrix eliminates the BRST surface terms, entailing the existence of an M9-brane behind the M2-brane with a hyper-critical flux.
Now, turning on the ‘789’ flux constraint, the gluing matrix:
![]()
allows us to derive:
![]()
![]()
which entail that the following holds:
![]()
when the following holds:
![]()
a condition that eliminates the BRST surface terms. In this gauge, ![]() and
and ![]() are represented as:
are represented as:
![]()
A commutative M9-brane is defined by:
![]()
precisely when we have ![]() and in the case of
and in the case of ![]() , we have:
, we have:
![]()
and the Ramond-Ramond gauge potential ![]() dual to the gauge potential
dual to the gauge potential ![]() couples to a D6-brane defined by a harmonic
couples to a D6-brane defined by a harmonic ![]() -form which is transverse to the worldvolume
-form which is transverse to the worldvolume ![]() and is magnetically charged w.r.t.
and is magnetically charged w.r.t. ![]() and is determined by:
and is determined by:
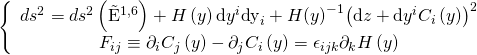
which, by dimensional reduction, leads to a D6-brane solution with a Kaluza-Klein monopole boundary that vanish inside the M9-brane. Hence, NC M9-branes can be naturally interpreted as bound states of M9-branes and KK monopoles.
Hence, a key consequence is that NC M-branes are BPS states. To realize that the action:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{S}_{{PS}}}=\int\limits_{\Sigma }{{{{\text{d}}^{3}}}}\tau \left[ {{{{\tilde{P}}}_{\mu }}\Pi _{0}^{\mu }+{{{\tilde{\mathcal{L}}}}_{{WZ}}}+{{d}_{\alpha }}{{\partial }_{0}}{{\theta }^{\alpha }}} \right.+{{w}_{\alpha }}{{\partial }_{0}}{{\lambda }^{\alpha }}+\left( {d{{\Gamma }_{\mu }}{{\partial }_{I}}\theta } \right)\Pi _{J}^{\mu }{{\epsilon }^{{IJ}}}\\-\frac{1}{2}\left( {{{{\tilde{P}}}^{\mu }}{{{\tilde{P}}}_{\mu }}+\det \left( {{{\Pi }_{I}}{{\Pi }_{J}}} \right)} \right)+{{e}^{I}}\left( {{{{\tilde{P}}}_{\mu }}\Pi _{I}^{\mu }+d{{\partial }_{I}}\theta +w{{\partial }_{I}}\lambda } \right)\\+\left( {w{{\Gamma }_{\mu }}{{\partial }_{I}}\lambda } \right)\Pi _{J}^{\mu }{{\epsilon }^{{IJ}}}-i{{\epsilon }^{{IJ}}}\left( {w{{\Gamma }_{\mu }}{{\partial }_{I}}\theta } \right)\left( {\bar{\lambda }{{\Gamma }^{\mu }}{{\partial }_{J}}\theta } \right)+i{{\epsilon }^{{IJ}}}\left( {w{{\partial }_{I}}\theta } \right)\left. {\left( {\bar{\lambda }\,{{\partial }_{J}}\theta } \right)} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-bade2f0c3de3e57465c2296109891b4f_l3.png)
is invariant under the SUSY transformations:
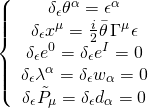
one carries partial integration, where in the open supermembrane under study here, such integration eliminates the surface boundary terms due to the SUSY constraints under consideration. The terms are derived from the WZ term:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l}{{{\tilde{\mathcal{L}}}}_{{WZ}}}={{\epsilon }^{{ijk}}}\left[ {\frac{1}{6}{{{\tilde{\mathcal{H}}}}_{{\mu \nu \rho }}}{{\partial }_{i}}{{x}^{\mu }}{{\partial }_{j}}{{x}^{\nu }}{{\partial }_{k}}{{x}^{\rho }}-\frac{i}{4}} \right.\left\{ {\bar{\theta }\,{{\Gamma }_{{\mu \nu }}}} \right.{{\partial }_{i}}\theta \,{{\partial }_{j}}{{x}^{\mu }}{{\partial }_{k}}{{x}^{\nu }}\\+\frac{i}{2}\bar{\theta }\,{{\Gamma }_{{\mu \nu }}}{{\partial }_{i}}\theta \bar{\theta }\,{{\Gamma }^{\mu }}{{\partial }_{i}}\theta \,{{\partial }_{k}}{{x}^{\nu }}-\frac{1}{{12}}\bar{\theta }\,{{\Gamma }_{{\mu \nu }}}{{\partial }_{i}}\theta \bar{\theta }\,{{\Gamma }^{\mu }}\left. {{{\partial }_{j}}\theta \bar{\theta }\,{{\Gamma }^{\nu }}\left. {{{\partial }_{k}}\theta } \right\}} \right]\end{array}](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-90950f5ecc8a01a979b8d236c2b958cb_l3.png)
and take the following form:
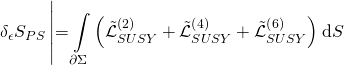
with:
![]()
![]()
![]()
Now, when one compares these terms with the BRST terms:
![]()
![]()
![]()
we get the following:
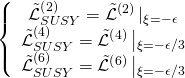
thus entailing that the BC that eliminate the PS surface terms also eliminate the BC of the SUSY surface terms, and so our NC M-branes preserve 16 supercharges and hence are 1/2 BPS entities, and whose centrality is that they allow us to apply Hitchin equations:
![]()
![]()
![]()
![]()
to the Hořava–Witten worldbrane hypersurface ![]() , which now read as:
, which now read as:
![]()
![]()
Now take any solution:
![]()
Then we can define:
![]()
Hence, for the class of ![]() gauge connections
gauge connections ![]() to which the solution descends, we have:
to which the solution descends, we have:
![]()
yielding:
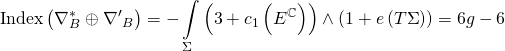
Thus, the first cohomology of our complex is:
![]()
Hence, we can now use the finiteness of the Tate-Shafarevich group to conclude that the pure spinor formalism, in light of the Tate algorithm and the F/M-theory duality, entails that M-theory is uniquely, up to isomorphism, the non-perturbative finite UV completion of the Standard Model of physics fully coupled to General Relativity.