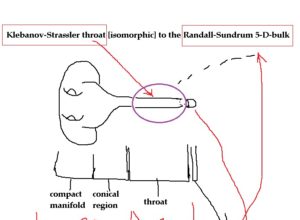
T-branes are supersymmetric intersecting brane configurations such that the non-Abelian Higgs field ![]() that describes D-brane deformations is not diagonalisable and satisfies nilpotency conditions where the worldvolume flux has non-commuting expectation values and their worldvolume adjoint Higgs field is given a VEV that cannot be captured by its characteristic polynomial, and thus derive their importance from the fact that heterotic string compactifications are dual to T-branes in F-theory. Let’s probe their dynamics. Starting with the D-term potential:
that describes D-brane deformations is not diagonalisable and satisfies nilpotency conditions where the worldvolume flux has non-commuting expectation values and their worldvolume adjoint Higgs field is given a VEV that cannot be captured by its characteristic polynomial, and thus derive their importance from the fact that heterotic string compactifications are dual to T-branes in F-theory. Let’s probe their dynamics. Starting with the D-term potential:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{{\hat V}_D} = \frac{1}{{2{\mathop{\rm Re}\nolimits} \left( {{f_h}} \right)}}{\left( {\sum\limits_j {{q_{{\phi _j}}}{\phi _j}\frac{{\partial K}}{{\partial {\phi _j}}} + M_P^2\sum\limits_j {{q_{hj}}} } } \right)^2}\\ = \frac{\pi }{{{\mathop{\rm Re}\nolimits} \left( {{T_h}} \right)}}{\left( {\sum\limits_j {{q_{{\phi _j}}}\frac{{{{\left| {{\phi _j}} \right|}^2}}}{s} - {\xi _h}} } \right)^2}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c9ec4ecd434d4bae8432fcfd42e4db82_l3.png)
with the ![]() -charge:
-charge:
![]()
and ![]() the gauge flux that yields the Fayet-Iliopoulos term:
the gauge flux that yields the Fayet-Iliopoulos term:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\frac{{{\xi _h}}}{{M_P^2}} = \frac{{{e^{ - \phi /2}}}}{{4\pi \mathcal{V}}}\frac{1}{{l_s^4}}\int_{{D_h}} {J \wedge {F^G}} = \frac{1}{{2\pi }}\sum\limits_j {\frac{{{q_{hj}}}}{\mathcal{V}}} \\ = - \sum\limits_j {{q_{hj}}} \frac{{\partial K}}{{\partial {T_j}}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-9bf658cb1cfe270f94e785956f4612d7_l3.png)
where the D-brane partition function for closed strings is given by:
![Rendered by QuickLaTeX.com \[P_{{\rm{int}}}^{Dp} \equiv Z = \sum\limits_{\gamma = 0}^\infty {\underbrace {\int {{D^K}\gamma {{D'}^K}X{e^{S_{cld}^s}}} }_{{\rm{Topologies}}}} \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4e2e5a5bba4fe487b08d9cf299490ba1_l3.png)
with a non-Abelian D-term:
![]()
and
![]()
is the first Pontryagin class-term, and ![]() is the flat space Kähler form:
is the flat space Kähler form:
![Rendered by QuickLaTeX.com \[J = \underbrace {\frac{i}{2}{\rm{dx}} \wedge {\rm{d\bar x + }}\frac{i}{2}{\rm{dy}} \wedge {\rm{d\bar y}}}_{ = :\omega } + 2i{\rm{dz}} \wedge {\rm{d\bar z}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-417733ad7b8551d8b3173be9dd53eec2_l3.png)
where ![]() is given by:
is given by:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{c}}{S_{cld}^s = - \frac{1}{{4\pi {\alpha ^\dagger }}}\int_{\partial E_S^5} {{d^2}\sigma d} \Omega {{\left( {{\phi _{Inst}}} \right)}^2}\sigma \sqrt { - \gamma } \left( {\phi \left( {{{\bar X}^\mu }} \right)} \right.R}\\{ + {\gamma ^{\alpha \beta }}{\partial _\alpha }{X^\mu }{g_{\mu \nu }}\left( {{{\bar X}^\nu }} \right) + \frac{1}{{\sqrt { - \gamma } }}{\varepsilon ^{ - {c_{2n}}/{Y_k}\left( {{{\cos }^2}\varphi } \right)}}{\partial _\beta }{{\bar X}^\nu }{b_{\mu \nu }}{{\left( {\bar X} \right)}^2}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-72921c00690470d9b037a6d7da26d27b_l3.png)
Then the non-Abelian profiles for ![]() and
and ![]() must satisfy the 7-brane functional equations of motion. Non-Abelian generalisation of:
must satisfy the 7-brane functional equations of motion. Non-Abelian generalisation of:
![]()
![]()
are built up as follows. Write locally:
![]()
and localize the integral in:
![]()
as:
![]()
thus, the non-Abelian generalisation of ![]() and
and ![]() have both the form of the D7-brane Chern-Simons action and hence satisfy the T-brane equation of motion.
have both the form of the D7-brane Chern-Simons action and hence satisfy the T-brane equation of motion.
So effectively, we have a Kähler-equivalence of the derivatives in the pull-back with gauge-covariant ones, yielding:
![]()
![]()
with ![]() the inclusion of the complex Higgs field
the inclusion of the complex Higgs field ![]() , and
, and ![]() represents the symmetrization over gauge indices.
represents the symmetrization over gauge indices.
In this local description, the Higgs field is given by:
![]()
where ![]() is a matrix in the complexified adjoint representation of
is a matrix in the complexified adjoint representation of ![]() and
and ![]() its Hermitian conjugate. Thus, locally, we have:
its Hermitian conjugate. Thus, locally, we have:
![]()
with:
![]()
a Kähler coordinate expansion of ![]() and gives us, after inserting it in:
and gives us, after inserting it in:
![]()
the following:
![]()
which is the exact 7-brane superpotential for F-theory and the integrand is independent of ![]() , entailing that the F-term conditions are purely topological and in no need for
, entailing that the F-term conditions are purely topological and in no need for ![]() -corrections
-corrections
Fixing our induced Dp-brane worldvolume metric:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{g_{ab}}\left( \xi \right) = {g_{\mu \nu }}\left( {x\left( \xi \right)} \right)\frac{{\partial {x^\mu }}}{{\partial {\xi ^a}}}\frac{{\partial {x^\nu }}}{{\partial {\xi ^b}}}\\ = {\eta _{ab}} + {\partial _a}{x^\mu }{\partial _b}{x_\mu } + \vartheta \left( {{{\left( {\partial x} \right)}^4}} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e81bde468b31c8219c65a749e71b3fd4_l3.png)
we can write the Dirac-Born-Infeld action as:
![Rendered by QuickLaTeX.com \[\begin{array}{c}{S_{DBI}} = - \frac{{{T_p}{{\left( {2\pi \alpha '} \right)}^2}}}{{4{g_s}}}\int {{d^{p + 1}}} \xi \left( {{F_{ab}}{F^{ab}} + \frac{2}{{{{\left( {2\pi \alpha '} \right)}^2}}}{\partial _a}{x^m}{\partial ^a}{x_m}} \right)\\ - \frac{{{T_p}}}{{{g_s}}}{V_{p + 1}} + \vartheta \left( {{F^4}} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-94ceb9803a2cb28862871fcc819700b3_l3.png)
which is a Higgsed ![]() gauge theory in
gauge theory in ![]() dimensions with
dimensions with ![]() scalar fields. Thus, by dimensional reduction, this action is equivalent to a
scalar fields. Thus, by dimensional reduction, this action is equivalent to a ![]() Yang-Mills gauge theory in 10-spacetime-dimensions with action:
Yang-Mills gauge theory in 10-spacetime-dimensions with action:
![]()
with:
![]()
and the action is invariant under the supersymmetric transformations:
![]()
with ![]() the infinitesimal Majorana-Weyl spinor. By double-gauging, we get our desired Dp-brane action:
the infinitesimal Majorana-Weyl spinor. By double-gauging, we get our desired Dp-brane action:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_{Dp}} = - \frac{{{T_p}{g_s}{{\left( {2\pi \alpha '} \right)}^2}}}{4}\int {{{\rm{d}}^{p + 1}}} \xi \left( {{F_{ab}}{F^{ab}} + 2{D_a}{\Phi ^m}{D^a}{\Phi _m}} \right.\\ + \sum\limits_{m \ne n} {{{\left[ {{\Phi ^m},{\Phi ^n}} \right]}^2}} \left. { + {\rm{fermions}}} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ea8441394a75356b23d67d92af934542_l3.png)
Crucially, note that the theory contains intersecting D2-D4-branes, since in the Casimir representation, the open string worldsheet boundary is a vertex vacuum connection coupled to a closed string state. This is the worldsheet-state correspondence in F-theory. Hence, the n-th loop open string Casimir force is equivalent to the n-th tree-level closed string charge exchange between two D-branes. It follows that the complete action of the Ramond-Ramond D-brane is an integral over the full space ![]() :
:
![Rendered by QuickLaTeX.com \[{S_{RR}} = - \frac{1}{4}\int\limits_X {G \wedge * G} - \sum\limits_i {\frac{{{\mu _i}}}{2}\int\limits_X {{\delta _{{\Sigma _i}}} \wedge \left( {C - G \wedge Y_i^{\left( 0 \right)}} \right)} } \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-7ebd65a8c28285e65f3aec6eb643be65_l3.png)
Hence, the gauged supergravity action is derivable as:
![Rendered by QuickLaTeX.com \[{\delta _G}{S_{RR}} = - \sum\limits_{i,j} {\frac{{{\mu _i}{\mu _j}}}{2}} \int\limits_X {{\delta _{{\Sigma _i}}} \wedge } \,\,{\delta _{{\Sigma _j}}} \wedge {\left( {{Y_i} \wedge {{\bar Y}_j}} \right)^{\left( 1 \right)}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-69246605eca291fca45916f9e660ac29_l3.png)
with:
![]()
and ![]() is the Ramond-Ramond potential, thus yielding the Chern-Simons action:
is the Ramond-Ramond potential, thus yielding the Chern-Simons action:
![Rendered by QuickLaTeX.com \[{S_{CS}} = \frac{{{T_p}}}{2}\int\limits_{{\Sigma _{p + 1}}} {C \wedge {\rm{ch}}\left( F \right)} \wedge \sqrt {\frac{{\hat A\left( {{R_T}} \right)}}{{\hat A\left( {{R_N}} \right)}}} \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-0d28857a8be6146ec36cc75a365b6029_l3.png)
The non-Abelian D-term thus takes the form:
![]()
In the local patch on the C-manifold, we take the flat-space-Kähler-form:
![Rendered by QuickLaTeX.com \[J = \underbrace {\frac{i}{2}{\rm{d}}x \wedge {\rm{d}}\bar x + \frac{i}{2}{\rm{d}}x \wedge {\rm{d}}\bar y}_{ = :\omega } + 2i{\rm{d}}z \wedge {\rm{d}}\bar z\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-719e7d63efe47a17c5e22d2b783d44d4_l3.png)
and decompose the Kähler-background B-field as:
![]()
with:
![]()
thus giving us:
![Rendered by QuickLaTeX.com \[\begin{array}{l}D = \int_{\tilde S} {S\left\{ {\rm{P}} \right.} \left[ J \right] \wedge \tilde F + \frac{{i\lambda }}{2}\left( {{\iota _\Phi }{\iota _\Phi }J} \right)\\ - \left( {{{\tilde F}^2} - {\omega ^2}} \right) - i\lambda \left( {{\iota _\Phi }{\iota _\Phi }B} \right)\omega \wedge \tilde F\\ - \omega \wedge {\rm{P}}\left[ {{B_{z\overline z }}{\rm{d}}z \wedge {\rm{d}}\bar z} \right]\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a0fe25124bde774846e7c3141c746fd2_l3.png)
with the Abelian pull-back ![]() to
to ![]() given by:
given by:
![Rendered by QuickLaTeX.com \[J = \underbrace {\frac{i}{2}{\rm{d}}x \wedge {\rm{d}}\bar x + \frac{i}{2}{\rm{d}}x \wedge {\rm{d}}\bar y}_{ = :\omega } + 2i{\rm{d}}z \wedge {\rm{d}}\bar z\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-719e7d63efe47a17c5e22d2b783d44d4_l3.png)
Hence we have:
![]()
Now: realize that ![]() is a zero-form and
is a zero-form and ![]() does not have transverse-legs to
does not have transverse-legs to ![]() , and thus the pull-back
, and thus the pull-back ![]() has a trivial action. So, after solving:
has a trivial action. So, after solving:
![]()
the D-term equations amount to ![]() with:
with:
![Rendered by QuickLaTeX.com \[\begin{array}{l}D = \int_{\tilde S} {S\left\{ {\omega \wedge \tilde F} \right.} + {\lambda ^2}{\rm{D}}\phi \wedge \overline {{\rm{D}}\phi } \\ \wedge \left( {2i\tilde F - {B_{z\overline z }}\omega } \right) + \lambda \left[ {\phi ,\bar \phi } \right]\\\left. {\left( {{\omega ^2} - {{\tilde F}^2} - i{B_{z\overline z }}\omega \wedge \tilde F} \right)} \right\}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-92ef74f7300fefeb087fd6471cca8ad1_l3.png)
and with the ![]() -field vanishing on the sheave of the C-manifold, one gets a reduction to:
-field vanishing on the sheave of the C-manifold, one gets a reduction to:
![]()
which yields a non-Abelian  -corrected Chern-Simons action for a stack of D7-branes with both terms at leading order in
-corrected Chern-Simons action for a stack of D7-branes with both terms at leading order in 
entailing that for matrix algebras:
![]()
they are the matrix products in the fundamental representation of 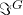
and so the ![]() -corrections on D-terms with the gauge flux F diagonalization yield the D-term equations:
-corrections on D-terms with the gauge flux F diagonalization yield the D-term equations:
![]()
Hence, the  -corrections are given entirely by the abelian pull-back of the Kähler-form
-corrections are given entirely by the abelian pull-back of the Kähler-form  to
to 
![]()
establishing a deep Wess–Zumino-based connection between T-branes and Abelian gauge field theory. This has vast implications for building realistic N/M-stack intersecting Dp-brane theories embedding the Standard Model of particle physics as well as that of cosmology.