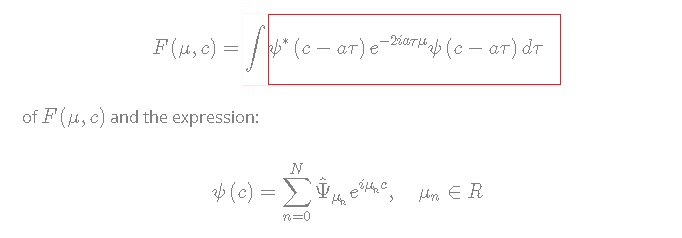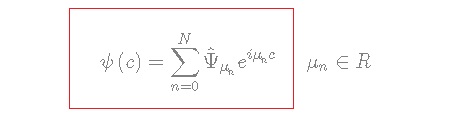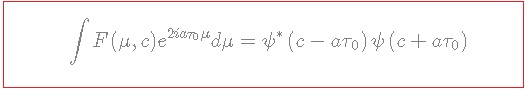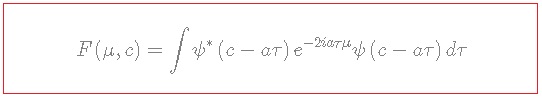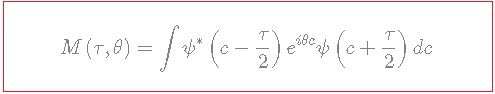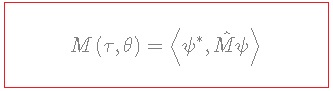I will derive a crucial property of loop quantum cosmology it shares with string/M-theory and asymptotically free quantum gravity theory, namely, that the associated Wigner-Moyal-Groenewold operator-formalism entails that the Holst-Barbero-Immirzi 4-spinfold has the property of spacetime uncertainty that I derived for string/M-theory, an essential property if loop quantum gravity is to be a valid quantum gravity theory. As I showed, in 4-D spacetime, the general relativistic starting point for canonical loop quantum gravity is given by:
![Rendered by QuickLaTeX.com \[\begin{array}{l}{S_{4{\rm{D}}}}\left[ {e',\omega } \right] = \int_{\tilde M} {\left( {\frac{1}{2}} \right.} {\rm{tr}}\left( {e \wedge e \wedge F} \right)\\\left. { + \frac{1}{\gamma }{\rm{tr}}\left( {e \wedge e \wedge * F} \right)} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6ff177d99b80a387dd34aa460f7067ea_l3.png)
where the dynamical variables are the tetrad one-form fields:
![]()
and the ![]() -valued connection
-valued connection ![]() whose curvature is:
whose curvature is:
![]()
and is a connection on the holonomy-flux algebra for a homogeneous isotropic Friedmann–Lemaître–Robertson–Walker ‘space’
Hence, we have the two-form:
![]()
with:
![]()
and ![]() is the Killing form on the Lie algebra
is the Killing form on the Lie algebra ![]() :
:
![]()
with
![]()
the totally antisymmetric tensor given by:
![]()
Now, I can write down the Holst action more informatively:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{{S_{4D}}\left[ {e,\omega } \right] = \int_{{{\tilde M}_4}} {{{\rm{d}}^4}} x{\varepsilon ^{\mu \nu \rho \sigma }}\left( {\frac{1}{2}} \right.{\varepsilon _{IJKL}}}\\{e_\mu ^Ie_\nu ^JF_{\rho \sigma }^{KL}\left. { + \frac{1}{\gamma }e_\mu ^Ie_\nu ^J{F_{\rho \sigma }}_{IJ}} \right)}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-5259c49f9f6455fd1438a77ef93a80e4_l3.png)
and from the Ashtekar variables, our action is:
![]()
![]()
with the Gaussian constraint:
![]()
the diffeomorphism constraint:
![]()
and our Hamiltonian is given by:
![Rendered by QuickLaTeX.com \[H = \frac{{8\pi G{\gamma ^2}}}{{\sqrt {\left| {\det \left( q \right)} \right|} }}{\tilde E^a}_A{\tilde E^b}_B\left[ {{\varepsilon ^{AB}}_C{F_{ab}}^C - \frac{{2\left( {1 + {\gamma ^2}} \right)}}{\gamma }{K_a}^A{K_b}^B} \right]\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-ccc665da907c8d12fe1f51f68e660577_l3.png)
The LQC Wigner-Moyal-Groenewold operator is the unique operator with the following properties:
![]()
![]() the LQC Holst-cylindrical functions and
the LQC Holst-cylindrical functions and ![]() the LQC characteristic function, the same as the Fourier transform of the the quasi probability density function of the group characters.
the LQC characteristic function, the same as the Fourier transform of the the quasi probability density function of the group characters.
It immediately follows from Fourier phase space symplecticity that the LQC Wigner-Moyal-Groenewold operator satisfies the following relation:
![]()
![]()
and for the LQC characteristic function, we have:
![]()
noting that any connection ![]() is gauge and diffeomorphism invariant in homogeneous isotropic space.
is gauge and diffeomorphism invariant in homogeneous isotropic space.
We can now define the holonomy-flux algebra for homogeneous isotropic Friedmann–Lemaître–Robertson–Walker space model via:
![]()
where the holonomy and the flux operators act as:
![]()
![]()
The Hilbert space basis is given by the connection-lifter LQG spin-networks:
![]()
with ![]() the configuration variable corresponding to the connection,
the configuration variable corresponding to the connection, ![]() the number of the Fourier fiducial cell repetition, and satisfy:
the number of the Fourier fiducial cell repetition, and satisfy:
![]()
and:
![]()
with ![]() a constant satisfying:
a constant satisfying:
![]()
Let us derive now the Wigner function and show that it satisfies the property that when integrated by one variable it reduces to the distribution density of the other variable. Define it as:
![]()
with:
![Rendered by QuickLaTeX.com \[\psi \left( c \right) = \sum\limits_{n = 0}^N {{{\hat \Psi }_{{\mu _n}}}{e^{i{\mu _n}c}}} ,\quad {\mu _n} \in R\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d68db5f40e8d798b1dfa7245bf33510f_l3.png)
For the distribution density function to be definable, the mutual quasi distribution function of ![]() and
and ![]() the following two equalities should be true:
the following two equalities should be true:
![]()
![]()
Hence, when integrating with respect to one variable it becomes the distribution density of the other one. The above equalities hold since our measures ![]() and
and ![]() satisfy:
satisfy:
![Rendered by QuickLaTeX.com \[\int\limits_{{{\hat R}_b}} {{{\hat f}_\mu }d\mu } = \sum\limits_{\mu \in R} {{{\hat f}_\mu }} \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-3e45f3582a104401564034b522b6d4d6_l3.png)
and:
![Rendered by QuickLaTeX.com \[\int\limits_{{R_b}} {{e^{i\mu c}}} dc = {\delta _{\mu ,0}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c2a1477a814e140a43012e575312e6fc_l3.png)
with ![]() the Bohr dual space and
the Bohr dual space and ![]() a Kronecker delta.
a Kronecker delta.
Now, the characters of the compactified line ![]() are the functions
are the functions ![]() , hence the Fourier transform of the function on
, hence the Fourier transform of the function on ![]() is given by:
is given by:
![]()
which is an isomorphism of:
![]()
and ![]() comprise the basis of:
comprise the basis of:
![]()
We need to prove the above equalities. First, substitute the expression:
![]()
of ![]() and the expression:
and the expression:
![Rendered by QuickLaTeX.com \[\psi \left( c \right) = \sum\limits_{n = 0}^N {{{\hat \Psi }_{{\mu _n}}}{e^{i{\mu _n}c}}} ,\quad {\mu _n} \in R\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d68db5f40e8d798b1dfa7245bf33510f_l3.png)
for ![]() into:
into:
![]()
giving us:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\int {F\left( {\mu ,c} \right)} \,d\mu = \int {\int {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\hat \Psi _{{\mu _n}}^ * } } } } {e^{ - ia{\mu _n}c}}\\{e^{ia{\mu _n}\tau }}{{\hat \Psi }_{{\mu _k}}}{e^{ia{\mu _k}c}}{e^{ia{\mu _k}\tau }}{e^{ - 2ia\tau \mu }}d\tau d\mu \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-7ef03859cac586e1514c51c377d40e50_l3.png)
with ![]() , and since integration with respect to
, and since integration with respect to ![]() is just a sum as
is just a sum as ![]() is discrete, we have:
is discrete, we have:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\int {F\left( {\mu ,c} \right)} \,d\mu = \sum\limits_{\mu \in R} {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\int {\hat \Psi _{{\mu _n}}^ * } } } } {e^{ - ia{\mu _n}c}}\\{e^{ia{\mu _n}\tau }}{{\hat \Psi }_{{\mu _n}}}{e^{ia{\mu _n}c}}{e^{ia{\mu _n}\tau }}{e^{ - 2ia\tau \mu }}d\tau \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-7d73f48b40a8dae15aea639e8612ad93_l3.png)
Now, using:
![Rendered by QuickLaTeX.com \[\int\limits_{{R_b}} {{e^{i\mu c}}} dc = {\delta _{\mu ,0}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c2a1477a814e140a43012e575312e6fc_l3.png)
and integrating with respect to ![]() , we can derive:
, we can derive:
![]()
Given ![]() , it follows that summation by
, it follows that summation by ![]() makes the terms with
makes the terms with ![]() equal to zero and the terms with
equal to zero and the terms with ![]() equal to one and all terms with
equal to one and all terms with ![]() and
and ![]() vanish from the sum. Hence, by using:
vanish from the sum. Hence, by using:
![Rendered by QuickLaTeX.com \[\psi \left( c \right) = \sum\limits_{n = 0}^N {{{\hat \Psi }_{{\mu _n}}}{e^{i{\mu _n}c}}} ,\quad {\mu _n} \in R\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d68db5f40e8d798b1dfa7245bf33510f_l3.png)
we derive:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\int {F\left( {\mu ,c} \right)} \,d\mu = \sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\hat \Psi _{{\mu _n}}^ * {e^{ - ia{\mu _n}c}}} } \\{{\hat \Psi }_{{\mu _k}}}{e^{ia{\mu _k}c}} = {\psi ^ * }\left( c \right)\psi \left( c \right) = {\left| {{\psi ^ * }\left( c \right)} \right|^2}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1ee42dee868fd9d74c04ef9b1f766b3d_l3.png)
and to prove the equality:
![]()
we substitute the expression:
![]()
of ![]() and the expression:
and the expression:
![Rendered by QuickLaTeX.com \[\psi \left( c \right) = \sum\limits_{n = 0}^N {{{\hat \Psi }_{{\mu _n}}}{e^{i{\mu _n}c}}} ,\quad {\mu _n} \in R\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d68db5f40e8d798b1dfa7245bf33510f_l3.png)
for ![]() into it, yielding:
into it, yielding:
![Rendered by QuickLaTeX.com \[{\int {F\left( {\mu ,c} \right)} {\mkern 1mu} d\mu = \int {\int {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\hat \Psi _{{\mu _n}}^*{e^{ - ia{\mu _n}c}}{e^{ia{\mu _n}\tau }}} {e^{ - 2ia\tau \mu }}d\tau dc} } } }\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2e8549ef8401fa3f49c362befc5e407e_l3.png)
Now, integration with measure ![]() given:
given:
![Rendered by QuickLaTeX.com \[\int\limits_{{R_b}} {{e^{i\mu c}}} dc = {\delta _{\mu ,0}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c2a1477a814e140a43012e575312e6fc_l3.png)
yields:
![]()
Hence, only the terms with ![]() remain in:
remain in:
![Rendered by QuickLaTeX.com \[{\int {F\left( {\mu ,c} \right)} {\mkern 1mu} d\mu = \int {\int {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\hat \Psi _{{\mu _n}}^*{e^{ - ia{\mu _n}c}}{e^{ia{\mu _n}\tau }}} {e^{ - 2ia\tau \mu }}d\tau dc} } } }\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2e8549ef8401fa3f49c362befc5e407e_l3.png)
and since integration with respect to ![]() gives us:
gives us:
![]()
And, from the last two equalities, it follows that:
![]()
then after substituting it into:
![Rendered by QuickLaTeX.com \[{\int {F\left( {\mu ,c} \right)} {\mkern 1mu} d\mu = \int {\int {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\hat \Psi _{{\mu _n}}^*{e^{ - ia{\mu _n}c}}{e^{ia{\mu _n}\tau }}} {e^{ - 2ia\tau \mu }}d\tau dc} } } }\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2e8549ef8401fa3f49c362befc5e407e_l3.png)
we can derive:
![]()
Hence, the integrals with respect to ![]() and
and ![]() are equal to one, yielding:
are equal to one, yielding:
![]()
So, from:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\int {F\left( {\mu ,c} \right)} \,d\mu = \sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\hat \Psi _{{\mu _n}}^ * {e^{ - ia{\mu _n}c}}} } \\{{\hat \Psi }_{{\mu _k}}}{e^{ia{\mu _k}c}} = {\psi ^ * }\left( c \right)\psi \left( c \right) = {\left| {{\psi ^ * }\left( c \right)} \right|^2}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1ee42dee868fd9d74c04ef9b1f766b3d_l3.png)
and:
![]()
it follows that ![]() is a LQC Wigner function in variables
is a LQC Wigner function in variables ![]() ,
, ![]() , completing the proof.
, completing the proof.
Next, we need to prove that the first momentum has the following property:
![]()
with ![]() . Start with substituting the red area:
. Start with substituting the red area:
into the left-hand-side of:
![]()
yielding:
![]()
By using the red-area expression below
for ![]() , we can deduce:
, we can deduce:
![Rendered by QuickLaTeX.com \[\begin{array}{*{20}{l}}{\int {F\left( {\mu ,c} \right)} {\mkern 1mu} {e^{2ia{\tau _0}\mu }}d\mu = \int {\int {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\hat \Psi _{{\mu _n}}^*} } } } {e^{ - ia{\mu _n}c}}{e^{ia{\mu _n}\tau }}}\\{{{\hat \Psi }_{{\mu _k}}}{e^{ia{\mu _k}c}}{e^{ia{\mu _k}\tau }}{e^{ - 2ia\tau \mu }}{e^{2ia{\tau _0}\mu }}d\tau d\mu }\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-dbff7acd9ae2359c71b154e62f959868_l3.png)
repeating the step above, integrating by ![]() can be replaced by summing over
can be replaced by summing over ![]() :
:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\int {F\left( {\mu ,c} \right)} \,{e^{2ia{\tau _0}\mu }}d\mu = \sum\limits_{\mu \in R} {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\int {\hat \Psi _{{\mu _n}}^ * } } } } {e^{ - ia{\mu _n}c}}{e^{ia{\mu _n}\tau }}\\{{\hat \Psi }_{{\mu _k}}}{e^{ia{\mu _k}c}}{e^{ia{\mu _k}\tau }}{e^{ - 2ia\tau \mu }}{e^{2ia{\tau _0}\mu }}d\tau \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a98b52a2b4c77d7d1f2eacaf60bbc2e9_l3.png)
and integrating by ![]() yields:
yields:
![]()
thus since the sum over ![]() equals one, we have:
equals one, we have:
![]()
substituting ![]() into it and using the definition of the LQC cylindrical functions:
into it and using the definition of the LQC cylindrical functions:
we get:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\int {F\left( {\mu ,c} \right)} \,{e^{2ia{\tau _0}\mu }}d\mu = \sum\limits_n {\sum\limits_k {\hat \Psi _{{\mu _n}}^ * } } {e^{ - ia{\mu _n}c}}{{\hat \Psi }_{{\mu _k}}}{e^{ia{\mu _k}c}}{e^{ia{\tau _0}\mu \left( {{\mu _n} + {\mu _k}} \right)}}\\ = {\psi ^ * }\left( {c - a{\tau _0}} \right)\psi \left( {c + a{\tau _0}} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4ac9eca3de3d5d45ecf86fa822b908de_l3.png)
Proving that the first momentum has the desired property:
Now, we need to show that the LQC Wigner-Moyal-Groenewold operator has the following property:
We substitute ![]() from:
from:
to obtain:
![]()
and by utilizing ![]() from our definition:
from our definition:
it reduces to:
![Rendered by QuickLaTeX.com \[\begin{array}{l}M\left( {\tau ,\theta } \right) = \int {\int {\int {\sum\limits_{n = 0}^N {\sum\limits_{k = 0}^K {\psi _{{\mu _0}}^ * } } } } } {e^{ - i{\mu _0}c}}{e^{ia{\mu _0}{\tau _0}}}\\{{\hat \Psi }_{{\mu _k}}}{e^{ - i{\mu _k}c}}{e^{ia{\mu _k}{\tau _0}}}{e^{ - 2ia{\tau _0}\mu }}d{\tau _0}{e^{i\tau \mu }}{e^{i\theta c}}d\mu dc\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6930c3db2b382bdccac951954703d26d_l3.png)
The same integration rules applied above go through now as well, yielding:
![]()
Combining the terms in the exponents and using the LQC cylindrical function above, we have:
![]()
Hence, we derived the LQC characteristic function ![]() as a Fourier transform of
as a Fourier transform of ![]() :
:
![]()
Now, we must prove that the following operator:
![]()
is a Wigner-Moyal-Groenewold operator, where:
![]()
We start by substituting
![]()
into:
yielding:
![]()
and expanding the exponents into the Taylor series allows us to derive:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\left\langle {{\psi ^ * },\hat M\psi } \right\rangle = \int {{\psi ^ * }} \left( c \right)\left( {1 + \frac{{i\tau }}{{2a}}\left( { - ia\frac{d}{{dc}} + ...} \right){e^{i\theta c}}} \right)\\\left( {1 + \frac{{i\tau }}{{2a}}\left( { - ia\frac{d}{{dc}} + ...} \right)\psi \left( c \right)dc} \right) = \int {{\psi ^ * }\left( {c - \frac{\tau }{2}} \right)} \,\psi \left( {c + \frac{\tau }{2}} \right)dc = M\left( {\tau ,\theta } \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-af3252078ef67166536df8e1ea7a0ece_l3.png)
amounting to a proof that:
![]()
is a Wigner-Moyal-Groenewold operator for a homogeneous and isotropic space whose connection-form is gauge and diffeomorphism invariant, and by the symplecticity of the associated LQG holonomy-flux algebra, the Holst-Barbero-Immirzi 4-spinfold has the property of space-time uncertainty:
![]()
with:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{\Delta {X_{imri}} \sim g_{LQG}^{1/3}{\ell _{LQG}}}\\{\Delta {T_{bar}} \sim g_{LQG}^{ - 1/3}{\ell _{LQG}}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d7e3bd19240b549dd2d4e6bf34d7542a_l3.png)