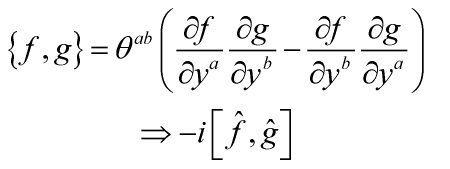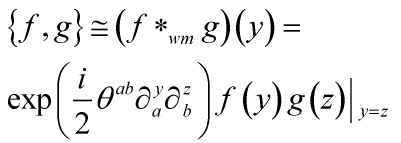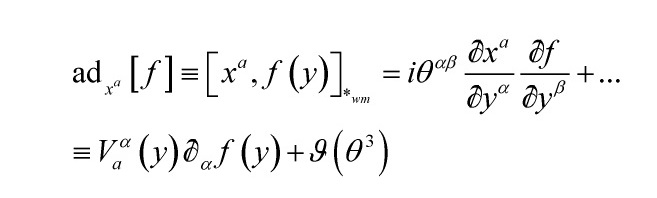It was Born who argued, correctly, that the geometric structure of quantized spacetime should reflect the same structure of the corresponding momentum space and that the phase space of values of a given quantum field is isomorphic to a nontrivial metaplectic manifold. This is true of string-theory, as the Tseytlin formulation entails. Recall, with ![]() a symplectic structure:
a symplectic structure:
![]()
one quantizes spacetime via its quantum-phase Poisson algebraic structure:
![]()
Hence, we have, for: ![]() , the following:
, the following:
Thus, the noncommutative algebra of operators is isomorphic to the deformed algebra of functions defined by the Weyl-Moyal product:
We then define a noncommutative space ![]() via the commutation relation:
via the commutation relation:
![]()
that allows us to interpret it as a noncommutative phase-space with Poisson structure given by ![]() .
.
Now, any field ![]() can be expanded in terms of the complete-operator-basis:
can be expanded in terms of the complete-operator-basis:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{{\rm A}_\theta } = \left\{ {\left| m \right\rangle \left\langle n \right|,n,m = 0,...} \right\}}\\{\hat \phi \left( {x,y} \right)\sum\limits_{n,m} {{M_{mn}}\left| m \right\rangle \left\langle n \right|} }\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-eb5a1144810721a74dd2339bb0b3dc49_l3.png)
with ![]() a C*-algebra, that is:
a C*-algebra, that is:
![]()
in infinitesimal form:
![]()
The coordinates ![]() in a gauge-theoretic setting will get promoted to the covariant coordinates defined by:
in a gauge-theoretic setting will get promoted to the covariant coordinates defined by:
![]()
and thus:
![]()
get covariantized as:
and from
![]()
we get a quantum-geometry relation:
![]()
constituting an orthonormal frame and defining vielbeins of a gravitational metric.
Since Darboux’s theorem in symplectic geometry is equivalent to the equivalence-principle in general relativity, it follows that the induced D-manifold defined by the metaplectic generalized quantum geometry continuously interpolates between a symplectic geometry![]() and a Riemannian geometry
and a Riemannian geometry![]() .
.
To justify Born’s thesis, let us simplify and work on a 4-D manifold ![]() and without loss of generality, a scalar field defined on it. The Hamiltonian in the Fourier representation is:
and without loss of generality, a scalar field defined on it. The Hamiltonian in the Fourier representation is:
![]()
with ![]() , and the phase-space for each mode
, and the phase-space for each mode ![]() is:
is:
![]()
with Poisson bracket ![]() and total field phase-space
and total field phase-space ![]() and with no loss of content, we can take:
and with no loss of content, we can take: ![]() . Our symplectic form is given by the area form
. Our symplectic form is given by the area form
![]()
locally:
![Rendered by QuickLaTeX.com \[\omega = \sum\limits_{i = 1}^n {{\rm{d}}{x^{n + i}}} \wedge {\rm{d}}{x^i}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-2f8dfdcace64f28d99d0ff5ba4cf689c_l3.png)
and the Hamiltonian vector field ![]() associated to a smooth function
associated to a smooth function ![]() can be locally written as:
can be locally written as:
![Rendered by QuickLaTeX.com \[{X_f} = \sum\limits_{i = 1}^n {\frac{{\partial f}}{{\partial {x^{n + i}}}}} \frac{\partial }{{\partial {x^i}}} - \frac{{\partial f}}{{\partial {x^i}}}\frac{\partial }{{\partial {x^{n + i}}}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-9c40a23b96bff10aae0b61612b9f666c_l3.png)
and for any smooth curve ![]() , the Hamilton-equation for the Hamiltonian
, the Hamilton-equation for the Hamiltonian ![]() is:
is:
![]()
Standard definition: with ![]() a diffeomorphism of a smooth manifold
a diffeomorphism of a smooth manifold ![]() onto itself, the canonical lift of
onto itself, the canonical lift of ![]() to the cotangent bundle is the transpose of the vector bundles isomorphism
to the cotangent bundle is the transpose of the vector bundles isomorphism
![]()
So, letting ![]() be the canonical lift of
be the canonical lift of ![]() to the cotangent bundle, we have for all
to the cotangent bundle, we have for all ![]() :
:
![]()
thus allowing us to derive:
![]()
and ![]() being the non-linearity scale and the covering angular coordinates being:
being the non-linearity scale and the covering angular coordinates being: ![]() and
and ![]() . The field variables
. The field variables ![]() are parametrizable in terms of
are parametrizable in terms of ![]() and
and ![]() as such:
as such:
![]()
with a dimensional constant. Our symplectic form reduces to:
![]()
with corresponding Poisson bracket:
![]()
and the spin-coordinates are:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{J_{\left( x \right)}}: = J\sin \theta \cos \varphi }\\{{J_{\left( y \right)}}: = J\sin \theta \sin \varphi }\\{{J_{\left( z \right)}}J\cos \theta }\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-207854486bba75c48290a18b95264d72_l3.png)
satisfying:
![]()
with the ![]() ‘s spanning the corresponding
‘s spanning the corresponding ![]() Lie algebra:
Lie algebra:
![]()
To derive a Hamiltonian that is globally well-defined, has the minimum ![]() and the correct linearized limit, one applies the analogy with a spin
and the correct linearized limit, one applies the analogy with a spin ![]() in a constant magnetic field
in a constant magnetic field ![]() and we postulate that the Hamiltonian has the form:
and we postulate that the Hamiltonian has the form:
![]()
with:
![]()
and:
![]()
Our Hamiltonian:
![]()
is hence recovered in the limit ![]() , up to an energy spectrum shift
, up to an energy spectrum shift ![]() . It follows from the brackets:
. It follows from the brackets:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\dot f = \left\{ {f,{H_{\rm{k}}}} \right\}\\f = {\phi _{\rm{k}}}\\{\pi _{\rm{k}}}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-3a775e4c6bd3f50b2a4d1903cd4f990f_l3.png)
that the Hamiltonian equations:
![Rendered by QuickLaTeX.com \[\left\{ {\begin{array}{*{20}{c}}{{{\dot \phi }_{\rm{k}}} = \sqrt {Jk} \tan \frac{{{\pi _{\rm{k}}}}}{{\sqrt {Jk} }}\cos \frac{{{\phi _{\rm{k}}}}}{{\sqrt {J/k} }}}\\{{{\dot \pi }_{\rm{k}}} = - \sqrt {Jk} k\sin \frac{{{\phi _{\rm{k}}}}}{{\sqrt {J/k} }}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1085e8a62fedcab39c1c4e842cd24f69_l3.png)
describing phase-space trajectories with parameters ![]() :
:
![]()
![]()
in the limit ![]() allow recovery of the classical expressions:
allow recovery of the classical expressions:
![]()
By Darboux’s theorem and:
![]()
we get the ![]() Lie algebra commutator:
Lie algebra commutator:
![]()
And for quantum states supported on field-values
![]()
one can expand ![]() in terms of
in terms of ![]() to derive the deformed commutation relation:
to derive the deformed commutation relation:
![]()
which is, and that’s where phase-space non-linearity comes in, the analytic dual to the generalized uncertainty principle:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\Delta {{\hat \phi }_{\rm{k}}}\Delta {{\hat \pi }_{\rm{k}}} \ge \\\frac{\hbar }{2}\left( {1 - \frac{k}{{2J}}{{\left( {\Delta {{\hat \phi }_{\rm{k}}}} \right)}^2} - \frac{1}{{2Jk}}{{\left( {\Delta {{\hat \pi }_{\rm{k}}}} \right)}^2}} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-851d1eb28f66b87a0db21109d8374e14_l3.png)
And furthermore, with the expansion at ![]() , one can expand
, one can expand ![]() and
and ![]() in terms of the creation and annihilation operators:
in terms of the creation and annihilation operators:
![Rendered by QuickLaTeX.com \[{\hat \phi _{\rm{k}}} = \sqrt {\frac{{\hbar J}}{{\left( {\hbar + 2J} \right)k}}} \left( {\hat a_{\rm{k}}^\dagger + {{\hat a}_{\rm{k}}}} \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a247ffa9ceee5cd3de317ef2620b9090_l3.png)
and:
![]()
Thus, by Darboux’s theorem, ![]() and
and ![]() generate a
generate a ![]() -deformed oscillator algebra:
-deformed oscillator algebra:
![]()
with the deformation parameter:
![]()
Hence, the quantized Hamiltonian:
![]()
with the ![]() -ordering-symmetry, yields the energy eigenvalues:
-ordering-symmetry, yields the energy eigenvalues:
![]()
with the eigenstates:
![Rendered by QuickLaTeX.com \[\begin{array}{l}\left| n \right\rangle = \left| {{n^{\left( 0 \right)}}} \right\rangle + {c_{n + 4}}\left| {{{\left( {n + 4} \right)}^{\left( 0 \right)}}} \right\rangle + \\{c_{n - 4}}\left| {{{\left( {n - 4} \right)}^{\left( 0 \right)}}} \right\rangle \left| {_{n\, \ge 4}} \right. + \vartheta \left( {{J^{ - 2}}} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c2d1154ebf81e2b37a1ae53b053fecef_l3.png)
with ![]() the zero-th order of the expansion, and the coefficients are given as:
the zero-th order of the expansion, and the coefficients are given as:
![]()
And the key relevance of this analysis to quantum geometry, and by extension, quantum gravity, is that the vacuum energy:
![]()
gets shifted by:
![]()
hence, the phase space of values of a given quantum field is isomorphic to a nontrivial metaplectic manifold