A String-Theoretic Derivation of Canonical General Relativity

By George Shiber Sunday, January 1, 2017Saturday, August 17, 2019 In Cosmology, Mathematical Physics, Mathematics, Philosophy, Philosophy Of Physics, Philosophy Of Science, Physics, Super String Theory, Supersymmetry Dirac-Hilbert Action, Einstein

Before discussing the canonical formulation of Einstein’s TGR and the relation it bears to string-dynamics and the critical relation between the total string-theory action and the Nieh–Yan-Barbero-Immirzi action, note that the Hilbert action is a functional of the metric tensor, given by:

${S_D} = {\int {\left( {^{\_\left( 4 \right)}g} \right)} ^{1/2}}{\,^{\left( 4 \right)}}R{d^4}x$

also note a crucial relation to the D-p-brane partition function for closed strings, which is:

$P_{{\rm{int}}}^{Dp} \equiv \not Z = \sum\limits_{\gamma = 0}^\infty {\underbrace {\int {{{\not D}^{SuSy}}\gamma {{\not D'}^{SuSy}}X{e^{S_{cld}^s}}} }_{{\rm{Topologies}}}}$

where ${\not D^{SuSy}}$ is the supersymmetry group covariant derivative. Since the closed string action satisfies the variational equation:

$\begin{array}{c}\delta S_{cld}^s = - \frac{1}{{2\pi \alpha '}}\int_{\partial E_S^5} {{d^2}} \sigma d\,\Omega {\left( {{\phi _{INST}}} \right)^2}{\varepsilon ^{\alpha \beta }}{{\not \partial }_\alpha }{X^\mu }{{\not \partial }_\mu }{\lambda _\nu }\\ = - \frac{1}{{2\pi \alpha '}}\int_{\partial E_S^5} {{d^2}} d\,\Omega {\left( {{\phi _{INST}}} \right)^{ - 1/2}}\sigma \,{{\not \partial }_\mu }X\nu {\left( {{\varepsilon ^{\alpha \beta }}{{\not \partial }_\beta }{X^{^\nu }}{\lambda _\mu }} \right)^{{e^{ - H_3^b}}}}\end{array}$

it follows that no topology in the sum is degenerate, and hence the closed string has a solvable action in 4-D curved space-time described by ${S_D}$ that needs no renormalization, where the closed string action coupled to the instanton field is:

$\begin{array}{*{20}{c}}{S_{cld}^s = - \frac{1}{{4\pi \alpha '}}\int_{\partial E_{{S_D}}^5} {{d^2}} \sigma d{\mkern 1mu} \Omega {\mkern 1mu} {{\left( {{\phi _{INST}}} \right)}^2}\sigma \sqrt { - \gamma } \left( {\phi \left( {\bar X} \right)} \right.{R_{icci}} + {\gamma ^{\alpha \beta }}{\partial _\alpha }{X^\mu }{g_{\mu \nu }}\left( {\bar X} \right)}\\{ + \frac{1}{{\sqrt { - \gamma } }}{\varepsilon ^{ - H_3^b}}{\partial _\alpha }{X^\mu }{\varepsilon ^{\alpha \beta }}{\partial _\beta }{X^\nu }{b_{\mu \nu }}{{\left( {\bar X} \right)}^2}}\end{array}$

Recall that in the canonical formalism for Einstein’s TGR as developed by Dirac and Arnowitt, Deser and Misner (ADM), standardly but wrongly identified with loop quantum gravity, the Hilbert action is a functional of the metric tensor, given by:

${S_D} = {\int {\left( {^{\_\left( 4 \right)}g} \right)} ^{1/2}}{\,^{\left( 4 \right)}}R{d^4}x$

${g_{\mu \nu }}(x),\quad x \in {\mathbb{R}^4}$

A central property of the Hilbert action is that one can add a divergence term to the integrand in:

${S_D} = {\int {\left( {^{\_\left( 4 \right)}g} \right)} ^{1/2}}{\,^{\left( 4 \right)}}R{d^4}x$

by substituting the Dirac-ADM Lagrangian density:

$L_D^{adm} = {\left( {^{ - (4)}g} \right)^{1/2}}{\,^{(4)}}R + \frac{{\partial {{\tilde V}^\alpha }}}{{\partial {x^\alpha }}}$

thus eliminating all occurrences of second derivatives of ${g_{\mu \nu }}$ and no first-time derivatives of ${g_{0\mu }}$ . The important point being is that ${g_{0\mu }}$ have vanishing conjugate momenta and occur in the theory as arbitrary functions, thus the remaining degrees of freedom are those represented by the spatial metric components ${g_{ij}}$ and their conjugates ${\pi ^{ij}}$ , and both fields are related as:

$\begin{array}{l}{{\rm H}_ \bot } = {g^{ - 1/2}}\left( {{\pi _{ij}}{\pi ^{ij}} - \frac{1}{2}{{\left( {\pi _j^i} \right)}^2}} \right) - \\{g^{1/2}}/R \approx 0\end{array}$

and

${{\rm H}_i} = - 2{\pi _i}^j\left| {_j} \right. \approx 0$

the geometric upshot is that 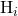${{\rm H}_i}$ generate arbitrary reparametrizations of the spacelike hypersurface on which the state is defined and 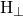${{\rm H}_ \bot }$ generate deformations that change the location of the hypersurface in the ambient spacetime

Hence, the hypersurfaces are embedded in a common spacetime, mathematically expressed by the following relations:

$\begin{array}{l}\left[ {{{\rm H}_ \bot }\left( x \right),{{\rm H}_ \bot }\left( {x'} \right)} \right] = \left( {{g^{rs}}\left( x \right){{\rm H}_s}\left( x \right)} \right.\\ + {g^{rs}}\left( {x'} \right)\left. {{{\rm H}_s}\left( {x'} \right)} \right){\delta _{,r}}\left( {x,x'} \right)\end{array}$

$\left[ {{{\rm H}_r}\left( x \right),{{\rm H}_ \bot }\left( {x'} \right)} \right] = {{\rm H}_ \bot }\left( x \right){\delta _{,r}}\left( {x,x'} \right)$

and

$\begin{array}{l}\left[ {{{\rm H}_r}\left( x \right),{{\rm H}_s}\left( {x'} \right)} \right] = {{\rm H}_r}\left( {x'} \right){\delta _{,s}}\left( {x,x'} \right)\\ + {{\rm H}_s}\left( x \right){\delta _{,s}}\left( {x,x'} \right)\end{array}$

Theoretically, then, one can fix the gauges by imposing certain coordinate conditions on the surface and by fixing the time-slicing. Such double-fixing of the spacetime coordinates is equivalent to incorporating four extra constraints besides those imposed by:

$\begin{array}{l}{{\rm H}_ \bot } = {g^{ - 1/2}}\left( {{\pi _{ij}}{\pi ^{ij}} - \frac{1}{2}{{\left( {\pi _j^i} \right)}^2}} \right) - \\{g^{1/2}}/R \approx 0\end{array}$

namely, two independent pairs of canonical variables per space-point, and it is precisely their coordinate-fixing that still stands in the way of a consistent theory of canonical quantum gravity: we cannot fix the gauge freedom in such a way as to entail spacetime parametrization through coordinates, and more seriously, the Hamiltonian associated with the coordinate conditions cannot be written in closed form and appears as a non-local term in the canonical fields, and this is fatal to the corresponding quantum theory since the spacetime parametrization ordering must be solved ex-novo at each order of perturbation theory in the expression for the Hamiltonian.

Moreover, the gauge maximal slicing condition $\left( {{\pi ^i}_i = 0} \right)$ is incompatible with a proper parametrization of spacetime and hence we cannot define Poisson brackets as commutators since q-numbers appear non-trivially on the right hand side of the commutation relations.

Let us see how string-theoretic concepts can resolve the problems canonically in comparative terms.

Take $n + 1$ fields ${y^A}\left( {x,t} \right),\;x \in \mathbb{R}$ where ${y^A}$ parametrizes a two dimensional surface ${V_2}$ embedded in an N + 1 dimensional Minkowski space with metric:

$\begin{array}{l}d{s^2} = d\tilde y \cdot d\tilde y = {\eta _{AB}}d{y^A}d{y^B} = \\ - {\left( {d{y^0}} \right)^2} + {\sum\limits_1^N {\left( {d{y^A}} \right)} ^2}\end{array}$

where the 2-D surface is spanned by the 1-D string in the N + 1 dimensional space. The action is given by:

${S_s} = {\int {\left( {^{ - (2)}g} \right)} ^{1/2}}dx\,dt$

and

${\left( {^{ - (2)}g} \right)^{1/2}}dx\,dt$

is the area element on ${V_2}$ . The string has finite length at any hyper-time instance and exhibits Poincaré invariant boundary conditions at its ends: thus, it is a relativistic theory.

The canonical formalism imposed by

${S_s} = {\int {\left( {^{ - (2)}g} \right)} ^{1/2}}dx\,dt$

yields a vanishing canonical Hamiltonian given that time reparametrization invariance is satisfied, with the following constraints holding:

${{\rm H}_1} = \tilde \pi \cdot \frac{{\partial \tilde y}}{{\partial x}} \approx 0$

${{\rm H}_ \bot } = \frac{1}{2}{\left| {\frac{{\partial \tilde y}}{{\partial x}}} \right|^{ - 1}}\left( {{{\tilde \pi }^2} + {{\left( {\frac{{\partial \tilde y}}{{\partial x}}} \right)}^2}} \right) \approx 0$

Those constraints admit a geometric interpretation, namely,

they generate tangential and normal deformations of the string

satisfying the following three closure conditions:

$\begin{array}{l}\left[ {{{\rm H}_ \bot }\left( x \right),{{\rm H}_ \bot }\left( {x'} \right)} \right] = \left( {{{\left| {\frac{{\partial \tilde y}}{{\partial x}}} \right|}^{ - 2}}\left( x \right){{\rm H}_ \bot }\left( x \right) + {{\left| {\frac{{\partial \tilde y}}{{\partial x}}} \right|}^{ - 2}}\left( x \right){{\rm H}_1}\left( {x'} \right)} \right)\\\delta '\left( {x,x'} \right) + 2\left( {{{\left| {\frac{{\partial \tilde y}}{{\partial x}}} \right|}^{ - 3}}\left( {x'} \right){{\rm H}_ \bot }\left( x \right){{\rm H}_1}\left( x \right) + {{\left| {\frac{{\partial \tilde y}}{{\partial x}}} \right|}^{ - 3}}\left( {x'} \right){{\rm H}_1}\left( {x'} \right)} \right)\\\delta '\left( {x,x'} \right)\end{array}$

$\left[ {{{\rm H}_1}\left( x \right),{{\rm H}_ \bot }\left( {x'} \right)} \right] = {{\rm H}_ \bot }\left( x \right)\delta '\left( {x,x'} \right)$

$\left[ {{{\rm H}_1}\left( x \right),{{\rm H}_1}\left( {x'} \right)} \right] = \left( {{{\rm H}_1}\left( x \right) + {{\rm H}_1}\left( {x'} \right)} \right)\delta '\left( {x,x'} \right)$

Note the presence of the quadratic term in the constraints on the right hand side of:

It has universally weakly vanishing brackets, hence, from:

${{\rm{H}}_1} = \tilde \pi \frac{{\partial ({y^0} - {y^1} = t)y}}{{\partial x}} \approx 0$

it follows that all the strings are embedded in a common two dimensional Riemannian surface

Now, the problem of accounting for the above constraints and fixing the coordinate system on the Riemannian surface spanned by the string can be solved by introducing a system of null surfaces ${y^0} - {y^1} = t$ in ${R^{N + 1}}$ ; thus

mathematically reducing the problem to dealing with N − 1 independent modes per point on the string

After introducing a spacelike gauge ${y^0} = t$ , the Dirac field brackets are then given in the form of:

$\begin{array}{l}\left[ {\alpha _m^A,\alpha _n^B} \right] = m\,{\delta _{m, - m}}{\delta ^{AB}} + \\\sum\limits_{M \ne 0} {\frac{{mn}}{M}} \frac{1}{{{{\left( {{p^0}} \right)}^2}}}\alpha _{m - M}^A\alpha _{n + M}^B\end{array}$

with:

$\begin{array}{l}{y^A}\left( {x,t} \right) = {q^A} + {p^{At + i}} + \\\sum\limits_{n \ne 0} {\frac{1}{n}} \alpha _n^A\cos \left( {nx} \right){e^{ - {\mathop{\rm int}} }}\end{array}$

By solving, we get a relation between the fields $\left( {{y^A},{\pi _A}} \right)$ and the fundamental canonical variables of the theory. Take the DelGuidice-DiVecchia-Fubini operators, whose O-algebra is isomorphic to the algebra of creation-annihilation operators, that appear in the integral form:

$D_n^A = \frac{1}{2}\int\limits_\pi ^{2\pi } {\frac{{d{y^A}\left( {0,t} \right)}}{{dt}}} \exp \left( {n{{\left( {\tilde k \cdot \tilde p} \right)}^{ - 1}}\tilde k \cdot \tilde y\left( {0,t} \right)} \right)dt$

Our string model can now be systematically constructed from this algebra

The pseudo-Euclidean structure of ${R^{N + 1}}$ is necessary for the DelGuidice-DiVecchia-Fubini operator-algebra since one needs it to derive the orthonormal coordinates $\left( {x,t} \right)$ , from which the equations of motion can be explicitly solved as:

${y^A}\left( {x,t} \right) = {f^A}\left( {t - x} \right) + {f^A}\left( {t + x} \right)$

which is an equation that defines the Fourier transform of the DelGuidice-DiVecchia-Fubini operator.

It is obvious, due to the renormalization problem: 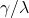$\gamma /\lambda$ -divergence, that a solution quasimorphic to the above equation cannot exist in Einstein’s TGR. Let us see what happens when we re-interpret canonical general relativity as a string-y theory

Let us posit a curved spacetime ${\Upsilon _4}$ embedded in a Minkowski space ${R^{N + 1}}$ with dimensionality $N \ge 9$ so we can incorporate a locally generic four-dimensional pseudo-Riemannian manifold, and where ${\Upsilon _4}$ is the home-space spanned by a 3-dimensional string. The major difference from the above is that the components of the metric ${g_{\mu \nu }}\left( x \right)$ are derived from the functions ${y^A}\left( {{x^0},{x^1},{x^2},{x^3}} \right)$ determining the time-dependent embedding of ${\Upsilon _3}$ in ${R^{N + 1}}$ , and thus are not basic variables, and are given by:

${g_{\mu \nu }}\left( x \right) = {\tilde y_{,\mu }} \cdot {\tilde y_{,\nu }} = {\eta _{AB}} = \frac{{\partial {{\tilde y}^A}}}{{\partial {{\tilde x}^\mu }}}\frac{{\partial {{\tilde y}^B}}}{{\partial {{\tilde y}^\nu }}}$

with:

$\left\{ {\begin{array}{*{20}{c}}{{\eta _{AB}} = {\rm{diag}}\left( { - 1,1,...,1} \right)}\\{A,B,... = 0...N}\end{array}} \right.$

Analogously with the action:

${S_D} = {\int {\left( {^{\_\left( 4 \right)}g} \right)} ^{1/2}}{\,^{\left( 4 \right)}}R{d^4}x$

we have the following Lagrangian action:

${S_D}\left[ y \right] = \int {\tilde L{d^4}} x$

with $\tilde L$ the Dirac-ADM Lagrangian density occurring in:

$L_D^{adm} = {\left( {^{ - (4)}g} \right)^{1/2}}{\,^{(4)}}R + \frac{{\partial {{\tilde V}^\alpha }}}{{\partial {x^\alpha }}}$

That $\tilde L$ has no time-derivatives of ${g_{0\alpha }}$ entails that only first-time-derivatives of ${y^A}$ enter into the action:

${S_D}\left[ y \right] = \int {\tilde L{d^4}} x$

A major obstacle is that insisting that the action be stationary under arbitrary variations of ${y^A}$ does not reproduce the equations of motion of Einstein’s theory of general relativity:

${\left( {^{tensor}{G_{Einstein}}} \right)^{\alpha \beta }} = {G^{\alpha \beta }} = 0$

instead, we get the problematic:

${G^{\alpha \beta }}{\tilde y_{;\alpha \beta }} = 0$

the string analogy:

${g^{\alpha \beta }}{\tilde y_{;\alpha \beta }} = 0$

where $\alpha$ and $\beta$ refer to the two dimensional Riemannian surface spanned by the string. The problem is that,

${\left( {^{tensor}{G_{Einstein}}} \right)^{\alpha \beta }} = {G^{\alpha \beta }} = 0$

does not entail ${G^{\alpha \beta }} = 0$ since the following identities hold:

${\tilde y_{;\alpha \beta }} \cdot {\tilde y_{,\gamma }} = 0$

The solution to recovering the full Einstein set of equations lies in imposing the additional constraints:

${G_{ \bot \,\alpha }} = 0$

where $\bot$ is the unit normal to ${\Upsilon _3}$ lying in ${\Upsilon _4}$ and $a = \bot ,1,2,3$ .

Fleshed-out, the Dirac-ADM Lagrangian density becomes:

$\tilde L = {g^{1/2}}N\left( {R + {K_{ab}}{K^{ab}} - {{\left( {K_a^a} \right)}^2}} \right)$

with $R$ the scalar curvature of ${\Upsilon _3}$ and ${K_{ab}}$ the extrinsic curvature of ${\Upsilon _3}$ given by:

${K_{ab}} = {\left( {2N} \right)^{ - 1}}\left( { - {{\dot g}_{ab}} + {N_{a\left| b \right.}} + {N_{b\left| a \right.}}} \right)$

with lapse and shift functions:

$\left\{ {\begin{array}{*{20}{c}}{N = {{\left( {^{ - (4)}{g^{00}}} \right)}^{1/2}}}\\{{N_a} = {g_{0a}}}\end{array}} \right.$

We now define the canonical momenta:

$\tilde \pi \left( x \right) = \frac{\delta }{{\delta \frac{{d\tilde y}}{{d{x^0}}}}}\int {{d^3}} x'\tilde L\left( {x'} \right)$

which yield:

$\tilde \pi = {g^{1/2}}\left( { - 2{G_{ \bot \, \bot }}\tilde n + 2\left( {{K^{ab}} - K_m^m{g^{ab}}} \right){{\tilde y}_{\left| {_{ab}} \right.}}} \right)$

with $\tilde n$ the unit normal to ${\Upsilon _3}$ lying in ${\Upsilon _4}$ :

$\tilde n = {N^{ - 1}}\left[ {\frac{{d\tilde y}}{{d{x^0}}} - \left( {\frac{{d{{\tilde y}^{\left| {_i} \right.}}{{\tilde y}_{,i}}}}{{d{x^0}}}} \right)} \right]$

and ${G_{ \bot \, \bot }}$ the double projection of the Einstein tensor along $\tilde n$ :

$- 2{G_{ \bot \, \bot }} = {K_{ab}}{K^{ab}} - {\left( {{K_m}} \right)^2} - R$

and we have:

$\tilde n \cdot \tilde n = - 1$

and the relation between the extrinsic curvature and $\tilde n$ is given by:

${K_{ab}} = \tilde n \cdot {\tilde y_{\left| {_{ab}} \right.}}$

Since the six-vectors ${\tilde y_{ab}}$ and $\tilde n$ are perpendicular to ${\Upsilon _3}$ and the three components of $\tilde \pi$ on ${\Upsilon _3}$ vanish, we get the constraints:

${{\rm H}_i} = \tilde \pi \cdot {\tilde y_{,i}} = 0$

which generate reparametrizations on ${\Upsilon _3}$ and satisfy the closure relations:

$\left[ {{{\rm H}_1}\left( x \right),{{\rm H}_ \bot }\left( {x'} \right)} \right] = {{\rm H}_ \bot }\left( x \right)\delta '\left( {x,x'} \right)$

$\left[ {{{\rm H}_1}\left( x \right),{{\rm H}_1}\left( {x'} \right)} \right] = \left( {{{\rm H}_1}\left( x \right) + {{\rm H}_1}\left( {x'} \right)} \right)\delta '\left( {x,x'} \right)$

hence, it follows that ${y^A}$ and ${\pi _A}$ transform as scalars and scalar-densities respectively under changes of coordinates in ${\Upsilon _3}$ . The needed fourth condition to:

${{\rm H}_1} = \tilde \pi \cdot \frac{{\partial \tilde y}}{{\partial x}} \approx 0$

for the string is obtained by solving:

$\tilde \pi = {g^{1/2}}\left( { - 2{G_{ \bot \, \bot }}\tilde n + 2\left( {{K^{ab}} - K_m^m{g^{ab}}} \right){{\tilde y}_{\left| {_{ab}} \right.}}} \right)$

as a system of nonlinear algebraic equations for ${n^A}$ as a function of ${\pi _A}$ and ${y^A}$ and imposing the normalization condition:

$\tilde n \cdot \tilde n = - 1$

Hence, the string counterpart of:

$\tilde \pi = {g^{1/2}}\left( { - 2{G_{ \bot \, \bot }}\tilde n + 2\left( {{K^{ab}} - K_m^m{g^{ab}}} \right){{\tilde y}_{\left| {_{ab}} \right.}}} \right)$

is:

$\tilde \pi = \left| {\frac{{\partial \tilde y}}{{\partial x}}} \right|\tilde n\left( {{\rm{string}}} \right)$

When ${G_{ \bot \, \bot }} = 0$ holds:

$\tilde \pi = {g^{1/2}}\left( { - 2{G_{ \bot \, \bot }}\tilde n + 2\left( {{K^{ab}} - K_m^m{g^{ab}}} \right){{\tilde y}_{\left| {_{ab}} \right.}}} \right)$

can be written as:

${\pi ^A} \approx W_B^A{n^A}$

with:

$W_B^A = 2{g^{1/2}}\left( {{g^{ad}}{g^{bc}} - {g^{ab}}{g^{cd}}} \right)y_{\left| {_{ab}} \right.}^A{y_{B\left| {_{cd}} \right.}}$

The matrix $W$ defined by the above equation can be interpreted as a mapping of ${R^{10}}$ onto ${R^{10}}$ , however, it does not have an inverse since it maps the three vectors ${\tilde y_{,i}}\left( {i = 1,2,3} \right)$ to zero. Note though that when restricted to the sub-space orthogonal to the ${\tilde y_{,i}}$ , $W$ will have an inverse. Let me refer to it as $M$ , and it is implicitly defined by yielding the solution of:

${\pi ^A} \approx W_B^A{n^A}$

namely:

${n^B} = M_A^B{\pi ^A}$

with the following property satisfied:

$\tilde n \cdot {\tilde y_{,i}} = 0$

Now, it follows from:

$W_B^A = 2{g^{1/2}}\left( {{g^{ad}}{g^{bc}} - {g^{ab}}{g^{cd}}} \right)y_{\left| {_{ab}} \right.}^A{y_{B\left| {_{cd}} \right.}}$

that $M$ is constructed from ${y^A}$ and their derivatives and:

${M_{AB}} = {\eta _{AC}}M_B^C$

is symmetric. The eight constraints of the theory are then:

$\begin{array}{l} - 2{G_{ \bot \, \bot }} = {K_{ab}}{K^{ab}} - {\left( {K_m^m} \right)^2} - R\\ \approx \frac{1}{2}{g^{ - 1/2}}{M_{AB}}{\pi ^A}{\pi ^B} - R \approx 0\end{array}$

$\begin{array}{l} - {G_{ \bot \,i}} = {\left( {K_i^kK_m^m\delta _i^k} \right)_{\left| k \right.}}\\ \approx {\left( {{M_{AB}}{\pi ^B}} \right)_{,i}}{y^{A\left| m \right.}}_{\left| m \right.} - {\left( {{M_{AB}}{\pi ^B}} \right)_{,m}}{y^{A\left| m \right.}}_{\left| i \right.} \approx 0\end{array}$

$\begin{array}{l}{{\rm H}_ \bot } = {g^{1/2}}\left( {{{\tilde n}^2} + 1} \right) \approx \\{g^{1/2}}\left( {{{\left( {{M^2}} \right)}_{AB}}{\pi ^A}{\pi ^B} + 1} \right) \approx 0\end{array}$

and

${{\rm H}_i} = \tilde \pi \cdot {\tilde y_{,i}} \approx 0$

Here’s the critical part: those constraints are homologically first-class and the connection to string-dynamics is that they exhibit $SU(2)$ –holonomy, namely, the multi-center Taub-NUT solutions are $U(1)$ -fibrations over ${\Upsilon _3}$ , with metric:

$d{s^2}_{TN} = Hd{\vec \tau ^2} + {H^{ - 1}}{\left( {d{x^{11}} + \vec C \cdot d\vec \tau } \right)^2}$

with:

$\left\{ {\begin{array}{*{20}{c}}{\nabla \times \vec C = - \nabla H}\\{H = \varepsilon + \frac{1}{2}\sum\limits_{i = 1}^{n + 1} {\frac{R}{{\left| {\vec \tau - {{\vec \tau }_i}} \right|}}} }\end{array}} \right.$

where

$H$

is harmonic on

${\Upsilon _3}$

and that is the string-y insight!

Hence, the supercovariant worldsheet action is:

$\begin{array}{l}{S_{C{\Upsilon _3}}} = \frac{1}{{2\pi \alpha '}}\int {{d^2}} z{d^2}\theta {g_{ab}}\left( \chi \right){D_{\bar \theta }}{\chi ^a}{D_\theta }{\chi ^b}\\ = \frac{1}{{2\pi \alpha '}}\int {{d^2}} z\left[ {{g_{ab}}\left( X \right)} \right.\partial {X^a}\bar \partial {X^b} + \\{g_{ab}}\left( {{\psi ^a}{D_{\bar z}}{\psi ^b} + {{\tilde \psi }^a}{D_z}{{\tilde \psi }^b}} \right) + \frac{1}{2}{R_{\mu \nu \rho \sigma }}\left( X \right)\left. {{\psi ^\mu }{\psi ^\nu }{{\tilde \psi }^\rho }{{\tilde \psi }^b}} \right]\end{array}$

and ${D_{\bar z}}{\psi ^a}$ and ${D_z}{\tilde \psi ^a}$ are the pull-backs of the Calabi-Yau connection to the string worldsheet, with the total string-theory action:

$\begin{array}{l}{S^{Total}} = \frac{1}{{2\pi {\alpha ^\dagger }12}}\int\limits_{{\rm{world - volumes}}} {{d^{26}}} x\,d\,\Omega {\left( {{\phi _{INST}}} \right)^2}\sqrt {\frac{{ - {g_{\mu \nu }}}}{{ - \gamma }}} \,{e^{ - {c_{2n}}/{\Upsilon _\kappa }(\cos \varphi )}} \cdot \\\left( {{R_{icci}} - 4{{\left( {{{\not D}^{SuSy}}\left( {{\phi _{INST}}} \right)} \right)}^2}} \right) + \frac{1}{{12}}H_{3,\mu \nu \lambda }^bH_3^{b,\mu \nu \lambda }/A_\mu ^H + \sum\limits_{D - p - branes} {S_{Dp}^{WV}} \end{array}$

By solving and orbifolding with respect to $\left( {SU\left( 2 \right)} \right)/{\Upsilon _3}$ , we get the 4-D ${\Upsilon _4}$ -connection to canonical general relativity via the Nieh–Yan-Barbero-Immirzi action:

$\begin{array}{l}^\dagger S_{NY}^{{\gamma _f}} = - \frac{1}{2}\int {{d^4}} x{\,^{(4)}}e\left[ {e_a^\mu } \right.e_b^\nu {\overline {{R_{\mu \nu }}} ^{ab}}\\ + \frac{{{\gamma _f}}}{2}{{\bar \nabla }_\mu }{S^\mu } + \frac{1}{{24}}{S_\mu }{S^\mu } - \frac{1}{3}{T_\mu }{T^\mu }\\ + \frac{1}{2}{q_{\mu \nu \rho }}\left. {{q^{_{\mu \nu \rho }}}} \right]\end{array}$

whose isomorphism-class is equivalent to that of general relativity.

The key to the derivation is that ${G_{ \bot \,\mu }}$ vanishes on hypersurfaces of ${\Upsilon _4}$ and that the following holds:

${G_{\alpha \beta }} = 0$

A String-Theoretic Derivation of Canonical General Relativity

the geometric upshot is that ${{\rm H}_i}$ generate arbitrary reparametrizations of the spacelike hypersurface on which the state is defined and ${{\rm H}_ \bot }$ generate deformations that change the location of the hypersurface in the ambient spacetime

they generate tangential and normal deformations of the string

it follows that all the strings are embedded in a common two dimensional Riemannian surface

mathematically reducing the problem to dealing with N − 1 independent modes per point on the string

Our string model can now be systematically constructed from this algebra

It is obvious, due to the renormalization problem: $\gamma /\lambda$ -divergence, that a solution quasimorphic to the above equation cannot exist in Einstein’s TGR. Let us see what happens when we re-interpret canonical general relativity as a string-y theory

The Cosmological Quantum State from Deformation Quantization

Spontaneous Quantum-to-Classical Cosmological Collapse Dynamics

About Me

Social Networks

Archives

Login Below

Photo Gallery

the geometric upshot is that generate arbitrary reparametrizations of the spacelike hypersurface on which the state is defined and generate deformations that change the location of the hypersurface in the ambient spacetime

they generate tangential and normal deformations of the string

it follows that all the strings are embedded in a common two dimensional Riemannian surface

mathematically reducing the problem to dealing with N − 1 independent modes per point on the string

Our string model can now be systematically constructed from this algebra

It is obvious, due to the renormalization problem: -divergence, that a solution quasimorphic to the above equation cannot exist in Einstein’s TGR. Let us see what happens when we re-interpret canonical general relativity as a string-y theory

The Cosmological Quantum State from Deformation Quantization

Spontaneous Quantum-to-Classical Cosmological Collapse Dynamics

RELATED

F-theory as the Modular Equivariant 12-D Lift of Type-IIB String Theory

Exceptional Field Theory and M-Theory on Kovalev TCS G2-Manifolds

The Wess–Zumino–Witten–Novikov Model, Taub-NUT Spaces, and M-Theory

About Me

Social Networks

Archives

Login Below

Photo Gallery

the geometric upshot is that ${{\rm H}_i}$ generate arbitrary reparametrizations of the spacelike hypersurface on which the state is defined and ${{\rm H}_ \bot }$ generate deformations that change the location of the hypersurface in the ambient spacetime

It is obvious, due to the renormalization problem: $\gamma /\lambda$ -divergence, that a solution quasimorphic to the above equation cannot exist in Einstein’s TGR. Let us see what happens when we re-interpret canonical general relativity as a string-y theory