Klebanov-Strassler warp-throat conifold-background will be the basis for our explicit analysis of warped D-brane inflationary cosmology
For a visual treat of the mathematical ‘picture’, scroll to the bottom of this post. In part two of this series on M-theoretic world-brane cosmology, I showed that a Klebanov-Strassler geometry naturally arises by considering string theory compactification on 
where 
is the Einstein manifold in five dimensions, with the interaction-Lagrangian of the massless Klebanov-Strassler field and the brane fields fermions is
![\[\begin{array}{c}{{\not L}^{KS}}_{\psi \bar \psi {H^0}}\frac{1}{{{M^{3/2}}}}\bar \psi \left[ {i{\gamma ^\mu }} \right.{\sigma ^{\mu \nu }}H_{\mu \nu \lambda }^0\left( {{x^\mu }} \right)\\\left. {\frac{{{\chi ^0}(r)}}{{\sqrt {\tau c} }}} \right]\psi \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f34d5cb329967b82724e34e08774d421_l3.png "Rendered by QuickLaTeX.com")
then I showed that after integrating over the extra dimensional part, the effective 4-D Lagrangian reduces to
![\[\begin{array}{c}\not L_{\psi \bar \psi {H^0}}^{KS} = i\bar \psi {\gamma ^\mu }{\sigma ^{\mu \nu }}\left[ {\frac{{{e^{ - 4\pi K/{3_{{g_s}}}M}}}}{{{M_{pl}}}}} \right. \cdot \\\left. {\left( {\frac{{{r_{\max }}}}{{{r_0}}}} \right)} \right]H_{\mu \nu \lambda }^0\psi \end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4fb159e826a96c1b6771b5777befc02e_l3.png "Rendered by QuickLaTeX.com")
with the fundamental Planck scale 
and the 4-D Planck scale 
related as
![\[{M_{pl}} = \frac{{{M^{3/2}}}}{{\sqrt {2R} }}{r_{\max }}{\left( {1 - \frac{{r_0^2}}{{r_{\max }^2}}} \right)^{1/2}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1d1ae592dee4246ec817f92c3979f106_l3.png "Rendered by QuickLaTeX.com")
Moreover, I demonstrated that the moduli spaces of compact Calabi-Yau spaces naturally contain conifold singularities and that the local description of these singularities is a conifold, a noncompact Calabi-Yau three-fold whose geometry is given by a cone, and that the orbifolded conifold equation
![\[\left\{ {\begin{array}{*{20}{c}}{C_{kl}^\wp :xy = {z^l}}\\{uv = {z^k}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4cad24e05e9e61ca7f4b23a09c43df01_l3.png "Rendered by QuickLaTeX.com")
allows us to consider the orbifolded conifold as a 
fibration over the 
plane and is a chiral theory with the gauge group
![\[\prod\limits_{i,j}^2 {SU{{(M)}_{i,j}}} \times \prod\limits_{i,j}^2 {SU{{(M)'}_{i,j}}} \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-364690add4c787c28716e5fc199b45a6_l3.png "Rendered by QuickLaTeX.com")
with
the deep part being that this AdS background is an explicit realization of the Randall-Sundrum scenario in string theory
that I discussed here and here. And so in line with the AdS/CFT duality, the 
geometry
has a dual gauge theory interpretation
namely, an 
gauge theory coupled to bifundamental chiral superfields, and adding D5-branes wrapped over the 
inside 
, the gauge group becomes
![\[SU\left( {N + M} \right){\rm{ }} \times {\rm{ }}SU\left( N \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-6675516688ab68568971f8bcd9021444_l3.png "Rendered by QuickLaTeX.com")
giving a cascading gauge theory. The three-form flux induced by the wrapped D5-branes – fractional D3-branes – satisfies
![\[\frac{1}{{{{\left( {2\pi } \right)}^2}\alpha '}}\int_{{S^3}} {{F_3}} = M\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1a01e2d7c6a6987816ea6c66364a6edb_l3.png "Rendered by QuickLaTeX.com")
and the Klebanov-Strassler warp-throat factor is
![\[\begin{array}{c}h(r) = \frac{{27\pi {{\left( {\alpha '} \right)}^2}}}{{4{r^2}}}\left[ {{g_s}} \right.N + \frac{2}{{2\pi }}\\{\left( {{g_s}M} \right)^2}{\rm{In}}\left( {\frac{r}{{{r_0}}}} \right) + \frac{3}{{8\pi }}\left. {{{\left( {{g_s}M} \right)}^2}} \right]\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-26f3bededdf075484e9cbb710a22ac3f_l3.png "Rendered by QuickLaTeX.com")
with
![\[{r_0} \sim {\varepsilon ^{2/3}}{e^{2\pi N/\left( {3{g_s}M} \right)}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-c423c677ff8f824b0cc22c3803f8e7fb_l3.png "Rendered by QuickLaTeX.com")
thus allowing explicit analysis of warped D-brane inflationary cosmology. Since M-theory remains the only promising paradigm for a corrective UV-completion of the Standard Model that also unifies gauge and gravitational interactions in a consistent quantum field theory, it is natural to analyze the theory for an explicit realization of inflationary cosmology. In small steps, in this post, let me do some 
warped-throat-analysis and set the stage for the next post on Klebanov-Strassler throat-analysis.
Now, the low-energy limit of type IIB superstring theory is type IIB supergravity, whose action is
![\[\begin{array}{c}S = \frac{{M_{10}^8}}{2}\int {{d^{10}}} x\sqrt { - g} \left( {R - \frac{{{{\left| {{{\not \partial }_\tau }} \right|}^2}}}{{2{{\left( {{\rm{Im}}\tau } \right)}^2}}}} \right.\\ - \frac{{{{\left| {{G_3}} \right|}^2}}}{{12{\rm{Im}}\tau }} - \left. {\widetilde F_5^2} \right) + \\\frac{{M_{10}^8}}{{8i}}\int {\frac{{{C_4} \wedge {G_3} \wedge {{\bar G}_3}}}{{{\rm{Im}}\tau }}} + fermions\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-172b749a0eb673d087f7b072a2f0b953_l3.png "Rendered by QuickLaTeX.com")
by which is meant ‘fermion-terms’, with 
the 10-d reduced Planck mass, and 
the 10-d Einstein frame metric with Ricci scalar 
, and 
is the axio-dilaton, formed from the Ramond-Ramond axion 
, with the dilaton 
defined by
![\[\tau = {C_0} + i{e^{ - \phi }}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-0d2eef27efaaf164c24293f6e67d344e_l3.png "Rendered by QuickLaTeX.com")
and 
the RR 4-form potential, whose field strength is 
. The fields 
and 
are constructed from the RR and Neveu-Schwarz 2-form potentials 
and 
with their respective field strengths 
and 
via
![\[{G_3} = {F_3} - \tau {H_3}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-4c4dea10ba4665a7d5424042a47b9021_l3.png "Rendered by QuickLaTeX.com")
and
![\[\begin{array}{c}{\widetilde F_5} = {F_5} - \frac{1}{2}{C_2} \wedge {H_3} + \\\frac{1}{2}{B_2} \wedge {F_3}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a78d78af314ed62dc5fae8e285552bec_l3.png "Rendered by QuickLaTeX.com")
and since one can include additional localized sources of flux and energy density, such as D-branes and orientifold-planes, in the background, then
can be supplemented by a piece 
from these sources, containing the tensions and couplings to the p-form fields. Hence, generally, for a compactification background which preserves 4-d Poincaré invariance, the metric can be parametrized as
![\[\begin{array}{c}d{s^2} = {e^{2A(y)}}{\eta _{\mu \nu }}d{x^\mu }d{x^\nu } + \\{e^{ - 2A(y)}}{\widetilde g_{mn}}d{y^m}d{y^n}\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-e322a9b42fb82770540e94c499084854_l3.png "Rendered by QuickLaTeX.com")
with 
is the 4-d Minkowski metric and 
are coordinates on a compact 6-d internal space and 
is the warp factor function. Note that can only have Picard-saddle-legs in the compact directions, and the self-dual must take the form
![\[{\widetilde F_5} = \left( {1 + * } \right)\left( {d\alpha (x) \wedge d{x^0} \wedge d{x^2} \wedge d{x^2} \wedge d{x^3}} \right)\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-1dd9544e08181900772943c9723d4930_l3.png "Rendered by QuickLaTeX.com")
for scalar function 
of the internal coordinates. Since antibranes break supersymmetry, and orientifold planes break 4-d N = 2 SUSY, which is preserved by a pure Calabi-Yau flux-compactification, to N = 1, throughout this post-series, I will tacitly assume a Calabi-Yau orientifold, which is N = 1 supersymmetric in 4-d setting. In the presence of additional antibranes, or for particular flux choices, SUSY may even be completely broken. Also, Poincaré invariant backgrounds contain localized objects such as D3 and D7-branes which fill the non-compact dimensions, or Euclidean D3-brane instantons wrapping 4-cycles in the internal manifold. If all objects in the background satisfy a BPS-like condition on their tensions, then is imaginary self-dual with respect to the 6-d internal metric
![\[{ * _6}{G_3} = i{G_3}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a2d22695d536929b979d4ff62fda8e3a_l3.png "Rendered by QuickLaTeX.com")
with the flux related to the warp factor as
![\[\alpha (y) = {e^{4A(y)}}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-d03b085dbd87e107700c77bde8f3e150_l3.png "Rendered by QuickLaTeX.com")
and to preserve 4-d N = 1 supersymmetry, must be a (2, 1)-form on the internal manifold.
This is crucial because in the 4-d effective theory, G3 flux on a Calabi-Yau compactification manifold M gives rise to a superpotential of Gukov-Vafa-Witten type
![\[W = \int_M {{G_3}} \wedge \Omega \]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-a64278942977e402456c9c69f73c0a3b_l3.png "Rendered by QuickLaTeX.com")
that I discussed here. Now, in type IIB
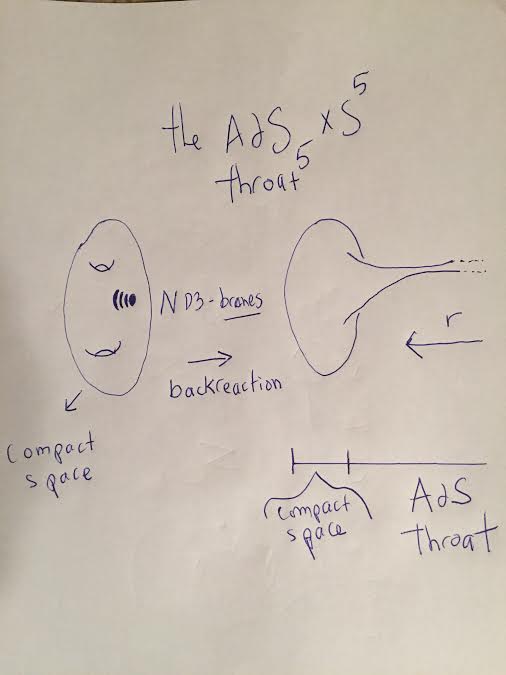
string compactifications to four dimensions, a warped-throat is a region of the internal space where the warp factor varies strongly along a particular direction and the classic model is the geometry near a stack of D3-branes. Placing N coincident D3-branes in 10-d flat spacetime will deform the metric to give
![\[\begin{array}{c}d{s^2} = H{(r)^{ - 1/2}}{\eta _{\mu \nu }}d{x^\mu }d{x^\nu } + \\h{(r)^{1/2}}\left( {d{r^2} + {r^2}ds_{{S^5}}^2} \right)\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-11f23f3800ee8cda75ef060d99d1ed24_l3.png "Rendered by QuickLaTeX.com")
with
![\[\left\{ {\begin{array}{*{20}{c}}{h(r) = 1\frac{{{R^4}}}{{{r^4}}}}\\{{R^4} = 4\pi {g_s}N{{\alpha '}^2}\frac{{{\pi ^3}}}{{{\rm{Vol}}\left( {{S^5}} \right)}} = 4\pi {g_s}N{{\alpha '}^2}}\end{array}} \right.\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-f185dd8867a24a8ce4095066310ecd89_l3.png "Rendered by QuickLaTeX.com")
visually
and this space is asymptotically flat as 
, given that 
. For small 
, the second term dominates, and the metric becomes that of
![\[\begin{array}{c}d{s^2} = \frac{{{r^2}}}{{{R^2}}}{\eta _{\mu \nu }}d{x^\mu }d{x^\nu } + \\\frac{{{R^2}}}{{{r^2}}}d{r^2} + {R^2}ds_{{S^5}}^2\end{array}\]](https://www.georgeshiber.com/wp-content/ql-cache/quicklatex.com-810609dfb73dcd1a63566f9f0c8a9ce2_l3.png "Rendered by QuickLaTeX.com")
with the branes sourcing N units of flux through the internal 
.
The AdS/CFT correspondence states that, for large N, classical supergravity on this background is dual to strongly coupled 4-d N = 4 SU(N) superYang-Mills theory and the conformality of the 4-d theory is reflected by translational invariance along the r direction of the 5-d AdS space and provides a stringy realization of the Randall-Sundrum-II model
This is deep, and next post I will apply to, and study, the Klebanov-Strassler throat.
